浙江省湖州市九校联合2021-2022学年中考数学押题卷含解析

这是一份浙江省湖州市九校联合2021-2022学年中考数学押题卷含解析，共18页。试卷主要包含了考生要认真填写考场号和座位序号，已知二次函数等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（共10小题，每小题3分，共30分）
1．如图，等腰直角三角板ABC的斜边AB与量角器的直径重合，点D是量角器上60°刻度线的外端点，连接CD交AB于点E，则∠CEB的度数为（ ）

A．60° B．65° C．70° D．75°
2．为了纪念物理学家费米，物理学界以费米（飞米）作为长度单位．已知1飞米等于0.000000000000001米，把0.000000000000001这个数用科学记数法表示为（　　）
A．1×10﹣15 B．0.1×10﹣14 C．0.01×10﹣13 D．0.01×10﹣12
3．已知A(x1，y1)，B(x2，y2)是反比例函数y＝(k≠0)图象上的两个点，当x1＜x2＜0时，y1＞y2，那么一次函数y＝kx－k的图象不经过(　　)
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．如图，等腰△ABC的底边BC与底边上的高AD相等，高AD在数轴上，其中点A，D分别对应数轴上的实数﹣2，2，则AC的长度为（　　）

A．2 B．4 C．2 D．4
5．如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（　　）

A．AE＝EC B．AE＝BE C．∠EBC＝∠BAC D．∠EBC＝∠ABE
6．下列图形中是轴对称图形但不是中心对称图形的是（　　）
A． B． C． D．
7．一元二次方程4x2﹣2x+=0的根的情况是（ ）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．无法判断
8．共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（　　）
A．1000（1+x）2＝1000+440 B．1000（1+x）2＝440
C．440（1+x）2＝1000 D．1000（1+2x）＝1000+440
9．已知二次函数（为常数），当自变量的值满足时，与其对应的函数值的最小值为4，则的值为（ ）
A．1或5 B．或3 C．或1 D．或5
10．函数y=中，自变量x的取值范围是（　　）
A．x＞3 B．x＜3 C．x=3 D．x≠3
二、填空题（本大题共6个小题，每小题3分，共18分）
11．七巧板是我国祖先创造的一种智力玩具，它来源于勾股法，如图①整幅七巧板是由正方形ABCD分割成七小块（其中：五块等腰直角三角形、一块正方形和一块平行四边形）组成，如图②是由七巧板拼成的一个梯形，若正方形ABCD的边长为12cm，则梯形MNGH的周长是　 　cm（结果保留根号）．

12．________.
13．如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y=的图象交于点D，且OD=2AD，过点D作x轴的垂线交x轴于点C．若S四边形ABCD=10，则k的值为　 　．

14．有五张分别印有等边三角形、正方形、正五边形、矩形、正六边形图案的卡片（这些卡片除图案不同外，其余均相同）．现将有图案的一面朝下任意摆放，从中任意抽取一张，抽到卡片的图案既是中心对称图形，又是轴对称图形的概率为_____．
15．等腰梯形是__________对称图形.
16．如图，在△ABC中，AD、BE分别是边BC、AC上的中线，AB=AC=5，cos∠C=，那么GE=_______．

三、解答题（共8题，共72分）
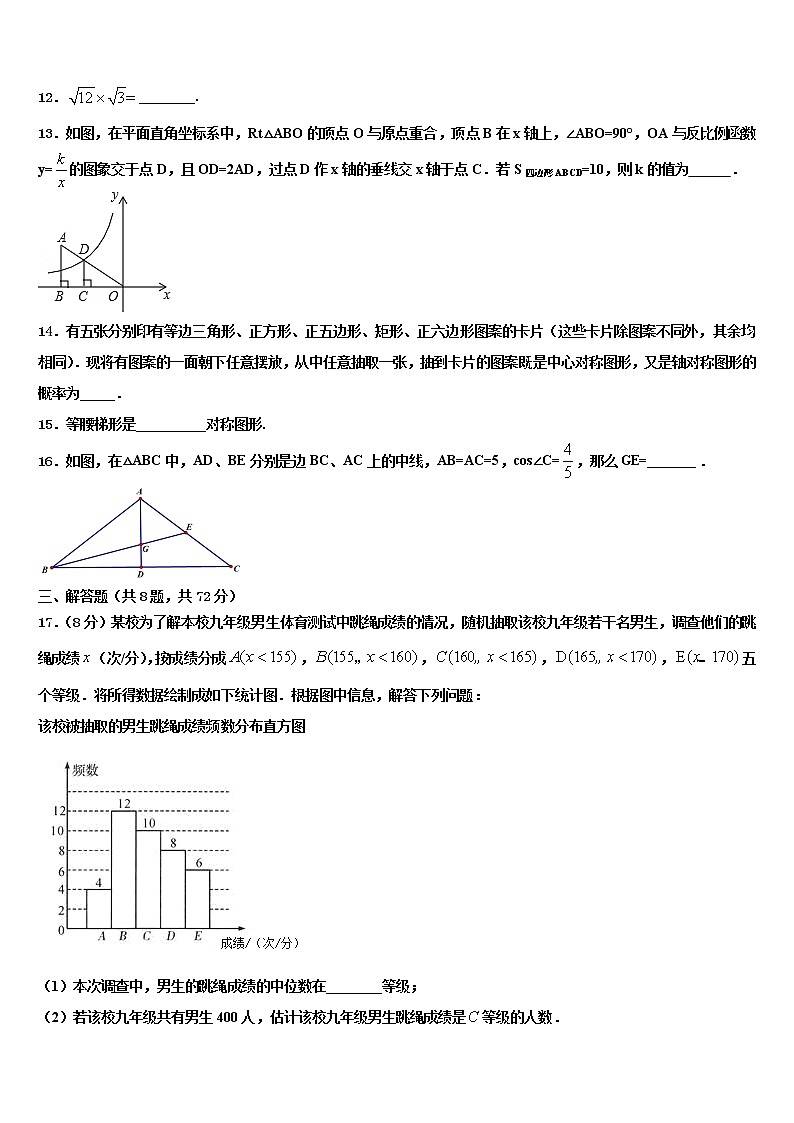
17．（8分）某校为了解本校九年级男生体育测试中跳绳成绩的情况，随机抽取该校九年级若干名男生，调查他们的跳绳成绩（次/分），按成绩分成，，，，五个等级．将所得数据绘制成如下统计图．根据图中信息，解答下列问题：
该校被抽取的男生跳绳成绩频数分布直方图

（1）本次调查中，男生的跳绳成绩的中位数在________等级；
（2）若该校九年级共有男生400人，估计该校九年级男生跳绳成绩是等级的人数．
18．（8分）如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．求证：四边形ACDF是平行四边形；当CF平分∠BCD时，写出BC与CD的数量关系，并说明理由．

19．（8分）某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，分别用、、表示；田赛项目：跳远，跳高分别用、表示．
该同学从5个项目中任选一个，恰好是田赛项目的概率为______；
该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．
20．（8分）（1）计算：﹣2sin45°+（2﹣π）0﹣（）﹣1；
（2）先化简，再求值•（a2﹣b2），其中a＝，b＝﹣2．
21．（8分） 截至2018年5月4日，中欧班列（郑州）去回程开行共计1191班，我省与欧洲各国经贸往来日益频繁，某欧洲客商准备在河南采购一批特色商品，经调查，用1600元采购A型商品的件数是用1000元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价少20元，已知A型商品的售价为160元，B型商品的售价为240元，已知该客商购进甲乙两种商品共200件，设其中甲种商品购进x件，该客商售完这200件商品的总利润为y元
（1）求A、B型商品的进价；
（2）该客商计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
（3）在（2）的基础上，实际进货时，生产厂家对甲种商品的出厂价下调a元（50＜a＜70）出售，且限定商场最多购进120件，若客商保持同种商品的售价不变，请你根据以上信息及（2）中的条件，设计出使该客商获得最大利润的进货方案．
22．（10分）如图，在▱ABCD中，点O是对角线AC、BD的交点，点E是边CD的中点，点F在BC的延长线上，且CF＝BC，求证：四边形OCFE是平行四边形．

23．（12分）《如果想毁掉一个孩子，就给他一部手机!》这是2017年微信圈一篇热传的文章．国际上，法国教育部宣布从2018年9月新学期起小学和初中禁止学生使用手机．为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是40人．

请你根据以上信息解答下列问题：在扇形统计图中，“玩游戏”对应的百分比为　 　，圆心角度数是　 　度；补全条形统计图；该校共有学生2100人，估计每周使用手机时间在2小时以上（不含2小时）的人数．
24．已知：如图，梯形ABCD，DC∥AB，对角线AC平分∠BCD，点E在边CB的延长线上，EA⊥AC，垂足为点A．
（1）求证：B是EC的中点；
（2）分别延长CD、EA相交于点F，若AC2=DC•EC，求证：AD：AF=AC：FC．




参考答案

一、选择题（共10小题，每小题3分，共30分）
1、D
【解析】
解：连接OD
∵∠AOD=60°，
∴ACD=30°.
∵∠CEB是△ACE的外角，
∴△CEB＝∠ACD+∠CAO=30°+45°=75°
故选：D

2、A
【解析】
根据科学记数法的表示方法解答.
【详解】
解：把这个数用科学记数法表示为．
故选：．
【点睛】
此题重点考查学生对科学记数法的应用，熟练掌握小于0的数用科学记数法表示法是解题的关键.
3、B
【解析】
试题分析：当x1＜x2＜0时，y1＞y2，可判定k＞0，所以﹣k＜0，即可判定一次函数y=kx﹣k的图象经过第一、三、四象限，所以不经过第二象限，故答案选B．
考点：反比例函数图象上点的坐标特征；一次函数图象与系数的关系．
4、C
【解析】
根据等腰三角形的性质和勾股定理解答即可．
【详解】
解：∵点A，D分别对应数轴上的实数﹣2，2，
∴AD＝4，
∵等腰△ABC的底边BC与底边上的高AD相等，
∴BC＝4，
∴CD＝2，
在Rt△ACD中，AC＝，
故选：C．
【点睛】
此题考查等腰三角形的性质，注意等腰三角形的三线合一，熟练运用勾股定理．
5、C
【解析】
解：∵AB=AC，∴∠ABC=∠ACB．∵以点B为圆心，BC长为半径画弧，交腰AC于点E，∴BE=BC，∴∠ACB=∠BEC，∴∠BEC=∠ABC=∠ACB，∴∠BAC=∠EBC．故选C．
点睛：本题考查了等腰三角形的性质，当等腰三角形的底角对应相等时其顶角也相等，难度不大．
6、C
【解析】
分析：根据轴对称图形与中心对称图形的概念求解．
详解：A、不是轴对称图形，也不是中心对称图形，故此选项错误；
B、是轴对称图形，也是中心对称图形，故此选项错误；
C、是轴对称图形，不是中心对称图形，故此选项正确；
D、不是轴对称图形，也不是中心对称图形，故此选项错误．
故选：C．
点睛：本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
7、B
【解析】
试题解析：在方程4x2﹣2x+ =0中，△=（﹣2）2﹣4×4× =0，
∴一元二次方程4x2﹣2x+=0有两个相等的实数根．
故选B．
考点：根的判别式．
8、A
【解析】
根据题意可以列出相应的一元二次方程，从而可以解答本题．
【详解】
解：由题意可得，
1000（1+x）2＝1000+440，
故选：A．
【点睛】
此题主要考查一元二次方程的应用，解题的关键是根据题意找到等量关系进行列方程.
9、D
【解析】
由解析式可知该函数在时取得最小值0，抛物线开口向上，当时，y随x的增大而增大；当时，y随x的增大而减小；根据时，函数的最小值为4可分如下三种情况：①若，时，y取得最小值4；②若-1＜h＜3时，当x=h时，y取得最小值为0，不是4；③若，当x=3时，y取得最小值4，分别列出关于h的方程求解即可．
【详解】
解：∵当x＞h时，y随x的增大而增大，当时，y随x的增大而减小，并且抛物线开口向上，
∴①若，当时，y取得最小值4，
可得：4，
解得或（舍去）；
②若-1＜h＜3时，当x=h时，y取得最小值为0，不是4，
∴此种情况不符合题意，舍去；
③若-1≤x≤3＜h，当x=3时，y取得最小值4，
可得：，
解得：h=5或h=1（舍）．
综上所述，h的值为-3或5，
故选：D．
【点睛】
本题主要考查二次函数的性质和最值，根据二次函数的性质和最值分类讨论是解题的关键．
10、D
【解析】
由题意得，x﹣1≠0，
解得x≠1．
故选D．

二、填空题（本大题共6个小题，每小题3分，共18分）
11、24+24
【解析】
仔细观察梯形从而发现其各边与原正方形各边之间的关系，则不难求得梯形的周长．
【详解】
解：观察图形得MH=GN=AD=12，HG=AC，
AD=DC=12，
AC=12，
HG=6．
梯形MNGH的周长=HG+HM+MN+NG=2HM+4HG=24+24．
故答案为24+24．
【点睛】
此题主要考查学生对等腰梯形的性质及正方形的性质的运用及观察分析图形的能力．
12、1
【解析】
先将二次根式化为最简，然后再进行二次根式的乘法运算即可．
【详解】
解：原式=2×=1．
故答案为1．
【点睛】
本题考查了二次根式的乘法运算，属于基础题，掌握运算法则是关键．
13、﹣1
【解析】
∵OD=2AD，
∴，
∵∠ABO=90°，DC⊥OB，
∴AB∥DC，
∴△DCO∽△ABO，
∴，
∴，
∵S四边形ABCD=10，
∴S△ODC=8，
∴OC×CD=8，
OC×CD=1，
∴k=﹣1，
故答案为﹣1．
14、
【解析】
判断出即是中心对称，又是轴对称图形的个数，然后结合概率计算公式，计算，即可．
【详解】
解：等边三角形、正方形、正五边形、矩形、正六边形图案中既是中心对称图形，又是轴对称图形是：正方形、矩形、正六边形共3种，
故从中任意抽取一张，抽到卡片的图案既是中心对称图形，又是轴对称图形的概率为：．
故答案为．
【点睛】
考查中心对称图形和轴对称图形的判定，考查概率计算公式，难度中等．
15、轴
【解析】
根据轴对称图形的概念，等腰梯形是轴对称图形，且有1条对称轴，即底边的垂直平分线．
【详解】
画图如下：

结合图形，根据轴对称的定义及等腰梯形的特征可知，
等腰梯形是轴对称图形.
故答案为：轴
【点睛】
本题考查了关于轴对称的定义，运用定义会进行判断一个图形是不是轴对称图形．
16、
【解析】
过点E作EF⊥BC交BC于点F，分别求得AD=3，BD=CD=4，EF=，DF=2，BF=6，再结合△BGD∽△BEF即可.
【详解】

过点E作EF⊥BC交BC于点F.
∵AB=AC， AD为BC的中线 ∴AD⊥BC ∴EF为△ADC的中位线.
又∵cos∠C=，AB=AC=5，∴AD=3，BD=CD=4，EF=，DF=2
∴BF=6
∴在Rt△BEF中BE==，
又∵△BGD∽△BEF
∴，即BG=.
GE=BE-BG=
故答案为.
【点睛】
本题考查的知识点是三角形的相似，解题的关键是熟练的掌握三角形的相似.

三、解答题（共8题，共72分）
17、（1）C;(2)100
【解析】
（1）根据中位数的定义即可作出判断；
（2）先算出样本中C等级的百分比，再用总数乘以400即可.
【详解】
解：（1）由直方图中可知数据总数为40个，第20，21个数据的平均数为本组数据的中位数，第20，21个数据的等级都是C等级，故本次调查中，男生的跳绳成绩的中位数在C等级；
故答案为C.
（2）400 =100（人）
答：估计该校九年级男生跳绳成绩是等级的人数有100人.
【点睛】
本题考查了中位数的求法和用样本数估计总体数据，理解相关知识是解题的关键.
18、（1）证明见解析；（2）BC=2CD，理由见解析.
【解析】
分析：（1）利用矩形的性质，即可判定△FAE≌△CDE，即可得到CD=FA，再根据CD∥AF，即可得出四边形ACDF是平行四边形；
（2）先判定△CDE是等腰直角三角形，可得CD=DE，再根据E是AD的中点，可得AD=2CD，依据AD=BC，即可得到BC=2CD．
详解：（1）∵四边形ABCD是矩形，
∴AB∥CD，
∴∠FAE=∠CDE，
∵E是AD的中点，
∴AE=DE，
又∵∠FEA=∠CED，
∴△FAE≌△CDE，
∴CD=FA，
又∵CD∥AF，
∴四边形ACDF是平行四边形；
（2）BC=2CD．
证明：∵CF平分∠BCD，
∴∠DCE=45°，
∵∠CDE=90°，
∴△CDE是等腰直角三角形，
∴CD=DE，
∵E是AD的中点，
∴AD=2CD，
∵AD=BC，
∴BC=2CD．
点睛：本题主要考查了矩形的性质以及平行四边形的判定与性质，要证明两直线平行和两线段相等、两角相等，可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上，通过证明四边形是平行四边形达到上述目的．
19、 (1);(2).
【解析】
（1）由5个项目中田赛项目有2个，直接利用概率公式求解即可求得答案；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好是一个田赛项目和一个径赛项目的情况，再利用概率公式即可求得答案．
【详解】
（1）∵5个项目中田赛项目有2个，∴该同学从5个项目中任选一个，恰好是田赛项目的概率为：．
故答案为；
（2）画树状图得：

∵共有20种等可能的结果，恰好是一个田赛项目和一个径赛项目的有12种情况，∴恰好是一个田赛项目和一个径赛项目的概率为：．
【点睛】
本题考查了用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
20、 (1)-2 (2)-
【解析】
试题分析：（1）将原式第一项被开方数8变为4×2，利用二次根式的性质化简第二项利用特殊角的三角函数值化简，第三项利用零指数公式化简，最后一项利用负指数公式化简，把所得的结果合并即可得到最后结果；
（2）先把和a2﹣b2分解因式约分化简，然后将a和b的值代入化简后的式子中计算，即可得到原式的值．
解：（1）﹣2sin45°+（2﹣π）0﹣（）﹣1
=2﹣2×+1﹣3
=2﹣+1﹣3
=﹣2；
（2）•（a2﹣b2）
=•（a+b）（a﹣b）
=a+b，
当a=，b=﹣2时，原式=+（﹣2）=﹣．
21、（1）80,100；（2）100件，22000元；（3）答案见解析.
【解析】
（1）先设A型商品的进价为a元/件，求得B型商品的进价为（a+20）元/件，由题意得等式 ，解得a＝80，再检验a是否符合条件，得到答案.
（2）先设购机A型商品x件，则由题意可得到等式80x+100（200﹣x）≤18000，解得，x≥100；再设获得的利润为w元，由题意可得w＝（160﹣80）x+（240﹣100）（200﹣x）＝﹣60x+28000，当x=100时代入w＝﹣60x+28000，从而得答案.
（3）设获得的利润为w元，由题意可得w（a﹣60）x+28000，分类讨论：当50＜a＜60时，当a＝60时，当60＜a＜70时，各个阶段的利润，得出最大值.
【详解】
解：（1）设A型商品的进价为a元/件，则B型商品的进价为（a+20）元/件，
，
解得，a＝80，
经检验，a＝80是原分式方程的解，
∴a+20＝100，
答：A、B型商品的进价分别为80元/件、100元/件；
（2）设购机A型商品x件，
80x+100（200﹣x）≤18000，
解得，x≥100，
设获得的利润为w元，
w＝（160﹣80）x+（240﹣100）（200﹣x）＝﹣60x+28000，
∴当x＝100时，w取得最大值，此时w＝22000，
答：该客商计划最多投入18000元用于购买这两种商品，则至少要购进100件甲商品，若售完这些商品，则商场可获得的最大利润是22000元；
（3）w＝（160﹣80+a）x+（240﹣100）（200﹣x）＝（a﹣60）x+28000，
∵50＜a＜70，
∴当50＜a＜60时，a﹣60＜0，y随x的增大而减小，则甲100件，乙100件时利润最大；
当a＝60时，w＝28000，此时甲乙只要是满足条件的整数即可；
当60＜a＜70时，a﹣60＞0，y随x的增大而增大，则甲120件，乙80件时利润最大．
【点睛】
本题考察一次函数的应用及一次不等式的应用，属于中档题，难度不大.
22、证明见解析.
【解析】
利用三角形中位线定理判定OE∥BC，且OE=BC．结合已知条件CF=BC，则OE//CF，由“有一组对边平行且相等的四边形为平行四边形”证得结论．
【详解】
∵四边形ABCD是平行四边形，∴点O是BD的中点．
又∵点E是边CD的中点，∴OE是△BCD的中位线，∴OE∥BC，且OE=BC．
又∵CF=BC，∴OE=CF．
又∵点F在BC的延长线上，∴OE∥CF，
∴四边形OCFE是平行四边形．
【点睛】
本题考查了平行四边形的性质和三角形中位线定理．此题利用了“平行四边形的对角线互相平分”的性质和“有一组对边平行且相等的四边形为平行四边形”的判定定理．熟记相关定理并能应用是解题的关键.
23、（1）35%，126；（2）见解析；（3）1344人
【解析】
(1)由扇形统计图其他的百分比求出“玩游戏”的百分比，乘以360即可得到结果；
(2)求出3小时以上的人数，补全条形统计图即可；
(3)由每周使用手机时间在2小时以上(不含2小时)的百分比乘以2100即可得到结果．
【详解】
(1)根据题意得：1﹣(40%+18%+7%)＝35%，
则“玩游戏”对应的圆心角度数是360°×35%＝126°，
故答案为35%，126；
(2)根据题意得：40÷40%＝100(人)，
∴3小时以上的人数为100﹣(2+16+18+32)＝32(人)，
补全图形如下：
；
(3)根据题意得：2100×＝1344(人)，
则每周使用手机时间在2小时以上(不含2小时)的人数约有1344人．
【点睛】
本题考查了条形统计图，扇形统计图，以及用样本估计总体，准确识图，从中找到必要的信息进行解题是关键.
24、（1）详见解析；（2）详见解析.
【解析】
（1）根据平行线的性质结合角平分线的性质可得出∠BCA=∠BAC，进而可得出BA=BC，根据等角的余角相等结合等角对等边，即可得出AB=BE，进而可得出BE=BA=BC，此题得证；
（2）根据AC2=DC•EC结合∠ACD=∠ECA可得出△ACD∽△ECA，根据相似三角形的性质可得出∠ADC=∠EAC=90°，进而可得出∠FDA=∠FAC=90°，结合∠AFD=∠CFA可得出△AFD∽△CFA，再利用相似三角形的性质可证出AD：AF=AC：FC．
【详解】
（1）∵DC∥AB，∴∠DCA=∠BAC．
∵AC平分∠BCD，∴∠BCA=∠BAC=∠DCA，∴BA=BC．
∵∠BAC+∠BAE=90°，∠ACB+∠E =90°，∴∠BAE=∠E，∴AB=BE，∴BE=BA=BC，∴B是EC的中点；
（2）∵AC2=DC•EC，∴．
∵∠ACD=∠ECA，∴△ACD∽△ECA，∴∠ADC=∠EAC=90°，∴∠FDA=∠FAC=90°．
又∵∠AFD=∠CFA，∴△AFD∽△CFA，∴AD：AF=AC：FC．

【点睛】
本题考查了相似三角形的判定与性质、角平分线的性质以及等腰三角形的性质，解题的关键是：（1）利用等角对等边找出BA=BC、BE=BA；（2）利用相似三角形的判定定理找出△AFD∽△CFA．