

2022年安徽省重点中学中考数学模拟诊断试卷(word版含答案)
展开2022年安徽省重点中学中考数学模拟诊断试卷
学校:___________姓名:___________班级:___________考号:___________
题号 | 一 | 二 | 三 | 四 | 总分 |
得分 |
|
|
|
|
|
一、选择题(本大题共10小题,共40分)
- 下列结论不正确的是( )
A. 不一定是负数 B. 当时,的倒数是
C. 的相反数是 D. 是正数
- 下列计算正确的是( )
A. B.
C. D.
- 把0.22×105改成科学记数法的形式,正确的是( )
A. B. C. D.
- 如图,是由五个相同的小正方体组成的立体图形,其俯视图是( )
A. B. C. D.
- 一元二次方程x2=4的根的情况为( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
- 下列调查中,适合普查的事件是( )
A. 调查华为手机的使用寿命
B. 调查你班学生打网络游戏的情况
C. 调查平顶山市七年级学生的心理健康情况
D. 中央电视台财经频道是真的吗的节目收视率
- 已知是一元二次方程的两个根中较大的根,则下面对的估计正确的是( )
A. B. C. D.
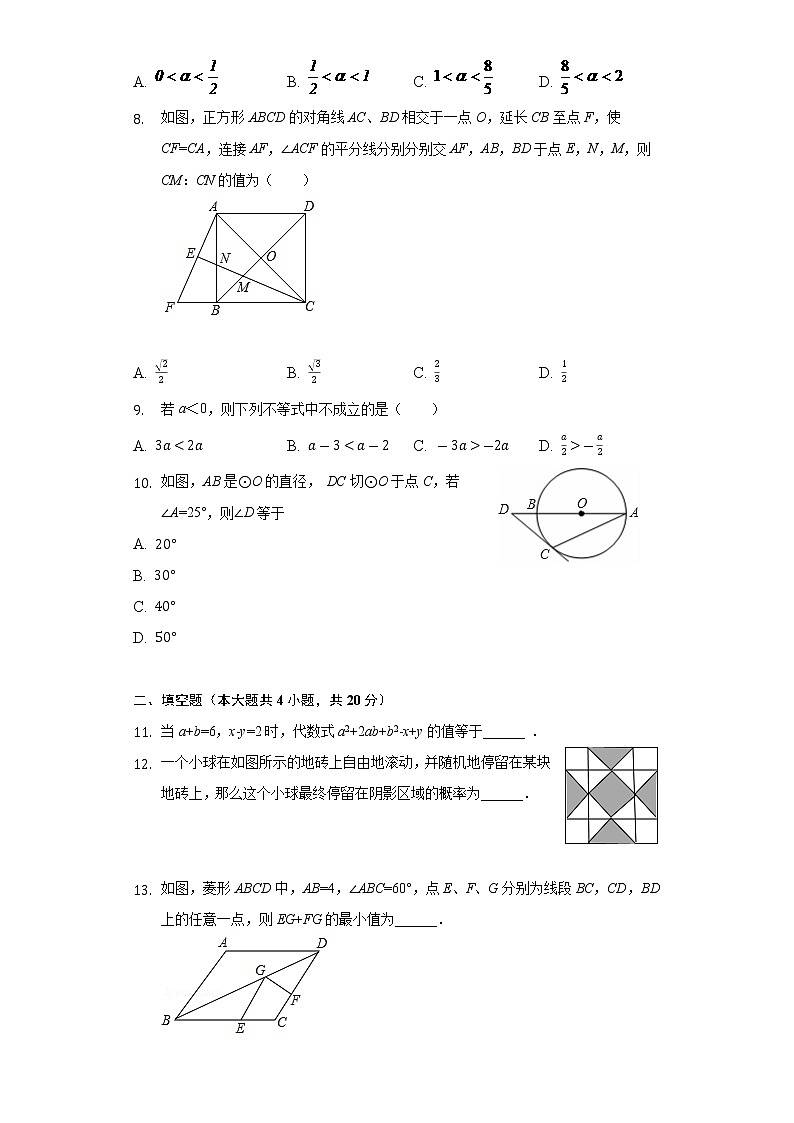
- 如图,正方形ABCD的对角线AC、BD相交于一点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别分别交AF,AB,BD于点E,N,M,则CM:CN的值为( )
A. B. C. D.
- 若a<0,则下列不等式中不成立的是( )
A. B. C. D.
- 如图,AB是⊙O的直径, DC切⊙O于点C,若∠A=25°,则∠D等于
A.
B.
C.
D.
二、填空题(本大题共4小题,共20分)
- 当a+b=6,x-y=2时,代数式a2+2ab+b2-x+y的值等于______ .
- 一个小球在如图所示的地砖上自由地滚动,并随机地停留在某块地砖上,那么这个小球最终停留在阴影区域的概率为______.
|
- 如图,菱形ABCD中,AB=4,∠ABC=60°,点E、F、G分别为线段BC,CD,BD上的任意一点,则EG+FG的最小值为______.
- 已知点A(4,y1),B(, y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1,y2,y3的大小关系是 .
三、计算题(本大题共1小题,共8分)
- (本题每小题6分,共l8分)
(1)计算:
(2)先化简,再求值:,其中=1,.
(3)解方程:
四、解答题(本大题共8小题,共82分)
- 计算:-4cos45°-()-1+|-1|.
- 如图,在平面直角坐标系中,△ABC的顶点C的坐标为(1,3).点A、B分别在格点上.
(1)直接写出 A、B两点的坐标;
(2)若把△ABC向上平移3个单位,再向右平移2个单位得△A′B′C′,画出△A′B′C′;
(3)若△ABC内有一点M(m,n),按照(2)的平移规律直接写出平移后点M的对应点M′的坐标.
- 如图,P1、P2是反比例函数y=(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)求反比例函数的解析式;
(2)求P2的坐标;
(3)过点P1、P2的两点作一直线l,求出当x取何值时,直线所表示的一次函数的函数值大于反比例函数y=(k>0)的函数值.
- 如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求的长.
、
- 如图,一栋大厦在迎街的墙面上垂挂了一长为50米的宣传条幅AE,刘明同学站在离大厦有一段距离的地面C处测得条幅顶端A的仰角为45°,测得条幅底端E的仰角为30°.求刘明同学是在距离该大厦多远的地方进行测量的?
|
- 甲市居民生活用水收费标准如表2,其中x是用水量(立方米),a和b是每立方米的单价(元).从2018年7月1日起,该市居民生活用水基本水价a将进行调整为b.小明对他家2018年两个月的水费进行统计,得到表1.
(表1)
月份 | 用水量 | 按调整 | 按调整 |
2 | 16 | 51.2 | 64 |
3 | 22 | 65.55 | 75.9 |
(表2)
| x≤20 | 20<x≤30 | x>30 |
调整前 | a | 1.5a | 2a |
调整后 | b | 1.5b | 2b |
请根据以上信息,回答以下问题:
(1)求基本水价调整提幅的百分率.
(2)小明家2017年7月的水费是144元,该月用水量若按调整后水价计费需缴多少元?
(3)小明查了有关资料发现:甲市取水点分散,引水管线合计300千米,而乙市只有一座水库供水,引水管线合计200千米.若两市每年每千米引水管线的运行成本都为150万元,乙市的现行基本水价为4元,甲市共有200万户家庭,乙市共有180万户家庭.若甲乙两市都按平均每户每月用水量为10立方米计算,请问甲市的基本水价至少调整为多少时甲市自来水公司的年收入(全市居民1年总水费-引水管线1年运行成本)不低于乙市?(精确到0.1元)
- 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).
(1)求抛物线的解析式;
(2)如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);
(3)在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.
- 如图,已知在△ABC中,AB=AC,BC比AB大3,sinB=,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90°时,直线PG与边BC相交于点M.求的值;
(3)当点Q在边AC上时,设BP=x,AQ=y,求y关于x的函数解析式,并写出它的定义域.
1.D
2.C
3.B
4.A
5.B
6.B
7.D
8.A
9.D
10.C
11.34
12.
13.2
14.y2< y1< y3
15.(1)原式=-57
(2)原式=-4
(3)
16.解:原式=2-4×-2+-1
=2-2-2+-1
=-3.
17.解:(1)A点的坐标(-1,-1),B点的坐标(4,2);
(2)(2)如图,△A′B′C′为所作;
(3)按照(2)的平移规律平移后点M的对应点M′的坐标为(m+2,n+3).
18.解:(1)过点P1作P1B⊥x轴,垂足为B,
∵点A1的坐标为(4,0),△P1OA1为等腰直角三角形,
∴OB=2,P1B=OA1=2,
∴P1的坐标为(2,2),
将P1的坐标代入反比例函数y=(k>0)得k=2×2=4,
∴反比例函数的解析式为y=;
(2)过点P2作P2C⊥x轴,垂足为C,
∵△P2A1A2为等腰直角三角形,
∴P2C=A1C,
设P2C=A1C=a,则P2的坐标为(4+a,a),
将P2的坐标代入反比例函数的解析式为y=,得
a=,
解得a1=2-2,a2=-2-2(舍去),
∴P2的坐标为(2+2,2-2);
(3)∵P1的坐标为(2,2),P2的坐标为(2+2,2-2),
由图可得,当2<x<2+2或x<0时,一次函数的函数值大于反比例函数的值.
19.解:(1)∵BC平分∠ABD,
∴∠DBC=∠ABC,
∵∠CAD=∠DBC,
∴∠CAD=∠ABC;
(2)∵∠CAD=∠ABC,
∴=,
∵AD是⊙O的直径,AD=6,
∴的长=××π×6=π.
20.解:过D点作DF⊥AB于F点,
在Rt△DEF中,设EF=x,∠EDF=30°
则tan30°==,DF=x,
在Rt△ADF中,∠EDF=45°,DF=,
则tan45°===1,
∴50+x=x,
解得:x=25(+1),
∴DF=75+25,
答:刘明同学在距离该大厦约75+25米处进行测量的.
21.解:(1)依题意,得:16a=51.2,16b=64,
解得:a=3.2,b=4.
∴×100%=×100=25%.
答:基本水价调整提幅的百分率为25%.
(2)144×(1+25%)=180(元).
答:该月用水量若按调整后水价计费需缴180元.
(3)设甲市的基本水价应调整为m元,
依题意,得:10m×12×200-150×300≥10×4×12×180-150×200,
解得:m≥4.225,
∴m的最小值为4.3.
答:甲市的基本水价至少调整为4.3元时,甲市自来水公司的年收入(全市居民1年总水费-引水管线1年运行成本)不低于乙市.
22.解:(1)设抛物线的表达式为:y=a(x-h)2+k=a(x-1)2+4,
将点C的坐标代入上式并解得:a=-1,
故抛物线的表达式为:y=-(x-1)2+4=-x2+2x+3①;
(2)点D的横坐标为m,则点D的坐标为(m,-m2+2m+3),
设直线AD的表达式为:y=kx+t,则,解得,
故直线AD的表达式为:y=-(m-3)x+3-m,
故点E(0,3-m),则CE=3-(3-m)=m,
则S=S△CED+S△CEA=CE×(xD-xA)=m(m+1)=m2+m;
(3)存在,理由:
在OB上截取OM=OA=1,故点M(1,0),
则∠MCO=∠ACO,
∵∠DAB=2∠ACO,
∴∠ACM=∠DAB,
在△ACM中,设CM边上的高为h,AC=MC==,
则S△AMC=AM×CO=×CM×h,即2×3=h,解得:h=,
在△ACM中,sin∠ACM====sin∠DAB,则tan∠DAB=,
在Rt△AOE中,OA=1,tan∠DAB=,
则OE=,故点E(0,),
由点A、E的坐标得,直线AE的表达式为:y=x+②,
联立①②并解得:x=或-1(舍去-1),
故x==m,故点D(,)
由(2)知,S=m2+m=,
∴点D的坐标为(,),相应的S的值为.
23.解:(1)在△ABC中,
∵AB=AC,点G是△ABC的重心,
∴BD=DC=BC,
∴AD⊥BC.
在Rt△ADB中,
∵sinB==,
∴=.
∵BC-AB=3,
∴AB=15,BC=18.
∴AD=12.
∵G是△ABC的重心,
∴AG=AD=8.
(2)在Rt△MDG,
∵∠GMD+∠MGD=90°,
同理:在Rt△MPB中,∠GMD+∠B=90°,
∴∠MGD=∠B.
∴sin∠MGD=sinB=,
在Rt△MDG中,∵DG=AD=4,
∴DM=,
∴CM=CD-DM=,
在△ABC中,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD.
∵∠QCM=∠CDA+∠DAC=90°+∠DAC,
又∵∠QGA=∠APQ+∠BAD=90°+∠BAD,
∴∠QCM=∠QGA,
又∵∠CQM=∠GQA,
∴△QCM∽△QGA.
∴==.
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF.
∵BE∥AD,∴=,即=,
∴BE=.
同理可得:=,即=,
∴CF=.
∵BE∥AD∥CF,BD=CD,
∴EG=FG.
∴CF+BE=2GD,即+=8,
∴y=,(0≤x≤).
2022年湖北省黄冈学校中考数学模拟诊断试卷(word版含答案): 这是一份2022年湖北省黄冈学校中考数学模拟诊断试卷(word版含答案),共14页。试卷主要包含了选择题,四象限B. 第一,解答题等内容,欢迎下载使用。
2022年湖北省黄冈学校中考数学模拟诊断试卷(word版含答案): 这是一份2022年湖北省黄冈学校中考数学模拟诊断试卷(word版含答案),共14页。试卷主要包含了选择题,四象限B. 第一,解答题等内容,欢迎下载使用。
2022年安徽省重点中学名校联盟中考数学模拟试卷(word版含答案): 这是一份2022年安徽省重点中学名校联盟中考数学模拟试卷(word版含答案),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












