2022年广东省中山市重点中学中考数学模拟试卷(word版含答案)

这是一份2022年广东省中山市重点中学中考数学模拟试卷(word版含答案)，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年广东省中山市重点中学中考数学模拟试卷学校:___________姓名：___________班级：___________考号：___________题号一二三总分得分      一、选择题（本大题共10小题，共30分）下列各数：中，无理数的个数是（　　）A. 个 B. 个 C. 个 D. 个中国首次火星探测任务天问一号探测器在2021年2月10日成功被火星捕获，成为中国第一颗人造火星卫星，并在距离火星约11000千米处，拍摄了火星全景图象.将11000用科学记数法表示应为（　　）A.  B.  C.  D. 等边三角形的对称轴有（　　）A. 条 B. 条或条 C. 条 D. 条某班主任对复课前一周班内20个利用业余时间学厨艺的学生的每日平均用时进行调查，结果如表：用时/h0.511.522.53人数/人365222则用时的中位数与众数分别为（　　）A. ， B. ， C. ， D. ，计算：（-ab3）2=（　　）A.  B.  C.  D. 已知等腰三角形一边长为2，一边长为4，则这个等腰三角形的周长为（　　）A.  B.  C.  D. 或下列不是必然事件的是（　　）A. 角平分线上的点到角两边距离相等
B. 三角形两边之和大于第三边
C. 面积相等的两三角形全等
D. 三角形外心到三个顶点距离相等若关于x的方程x2+2x-m+1=0有两个实数根，则实数m的取值范围是（　　）A.  B.  C.  D. 知在△ABC中，点D为AB上一点，过点DB线AC于点E，点E作AB平线交BCF．则下列说不正确的是（　　）A.
B.
C.
D. 已知二次函数y=（a-2）x2+ax-5的图象开口向上，则a的取值范围是（　　）A.  B.  C.  D.  二、填空题（本大题共7小题，共28分）在函数y=中，自变量x的取值范围是______．分解因式am2-an2=______．某校对八年级600名学生就“分组合作学习”方式的支持程度进行了调査，随机抽取了若干名学生进行调查，并制作统计图，据此统计图估计该校八年级支持“分组合作学习”方式的学生（含非常喜欢和喜欢两种情况）约为______名．
如图，已知矩形ABCD，一条直线把矩形分割成两个多边形，若两个多边形的内角和分别为M和N，则M+N的最小值为______ ．如图，在平面直角坐标系中，点A的坐标为（0,3），△OAB 沿x轴向右平移后得到△O′A′B′，点A的对应点在直线上一点，则点 B与其对应点B′间的距离为_____________.
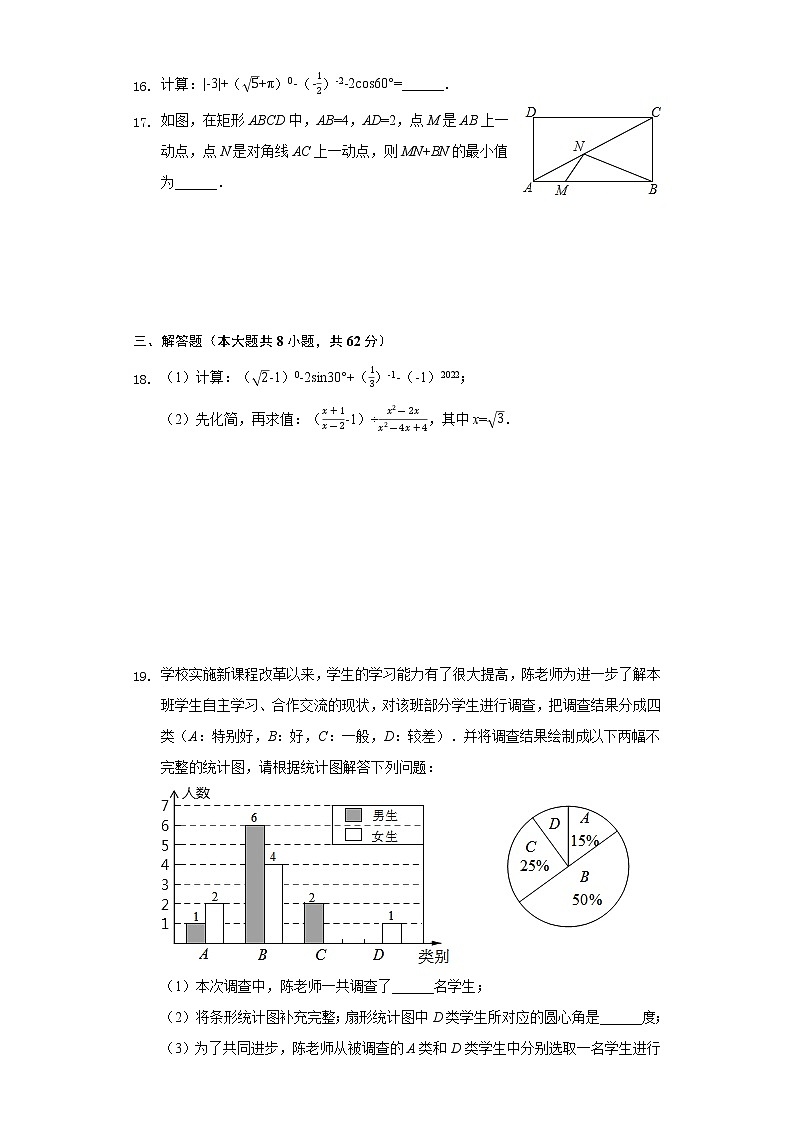
  计算：|-3|+（+π）0-（-）-2-2cos60°=______．如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为______．
​
    三、解答题（本大题共8小题，共62分）（1）计算：（-1）0-2sin30°+（）-1-（-1）2022；
（2）先化简，再求值：（-1）÷，其中x=．






 学校实施新课程改革以来，学生的学习能力有了很大提高，陈老师为进一步了解本班学生自主学习、合作交流的现状，对该班部分学生进行调查，把调查结果分成四类（A：特别好，B：好，C：一般，D：较差）．并将调查结果绘制成以下两幅不完整的统计图，请根据统计图解答下列问题：

（1）本次调查中，陈老师一共调查了______名学生；
（2）将条形统计图补充完整；扇形统计图中D类学生所对应的圆心角是______度；
（3）为了共同进步，陈老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习，请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率．






 平面内两条直线AB、CD交于点O，过点P作直线PM∥AB，PN∥CD．

  






 如图，四边形ABCD中，∠ADC=90°，点E为边BC上的一点，连接DE，点F为ED上的一点，连接AF、BF，且AB=AC，AD=AF，∠BAC=∠DAF．
（1）求证：∠BFE=∠CDE；
（2）若DE=9，CD=2，tan∠CDE=，求边BC的长．






 两种移动电话计费方式表：  全球通神州行月租50元/月0本地通话费0.4元/分0.6元/分（1）一个月在本地通话200分和300分，按两种计费方式各需交多少线？
（2）对于某个本地通话时间，会出现两种计费方式的收费一样的情况吗？
（3）张老师想办一张电话卡，请你给他点建议．






 一辆自行车竖直摆放在水平地面上如图所示，右边是它的示意图，横梁AC平行于水平面MN，现测得BC=80cm，∠CAB=60°，∠ACB=50°，B到MN的距离BE=30cm，AD为可调节高度，经研究发现，当坐垫高度为身高的0.6倍时，骑行者最舒适，现一身高170cm的同学骑车，当AD长约为多少时，可以使骑行者最舒适？（结果保留一位小数，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，≈1.73）







 平面直角坐标系xOy中，给出如下定义：对于图形G及图形G外一点P，若图形G上存在一点M，满足PM=2，且使点P绕点M顺时针旋转90°后得到的对应点P′在这个图形G上，则称点P为图形G的“2旋转点”．
已知点A（-1，0），B（-1，2），C（2，-2），D（0，3），E（2，2），F（3，0）．
（1）①判断：点B______线段AF的“2旋转点”（填“是”或“不是”）；
②点C，D，E中，是线段AF的“2旋转点”的有______；
（2）已知直线l：y=x+b，若线段l上存在线段AF的“2旋转点”，求b的取值范围；
（3）⊙T是以点T（t，0）为圆心，为半径的一个圆，已知在线段AD上存在这个圆的“2旋转点”，直接写出t的取值范围．







 如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，与y轴交于点C，点A的坐标为（-1，0），对称轴为直线x=1，点P为线段BC上（不含B、C两点）的一个动点，PF∥y轴交抛物线于点F，设点P的横坐标为m．
（1）求抛物线的解析式；
（2）用含m的代数式表示线段PF的长；
（3）设△BCF的面积为S，求S与m的函数关系式，并确定当m为何值时△BCF的面积最大．







 1.B
 2.C
 3.C
 4.C
 5.C
 6.C
 7.C
 8.A
 9.C
 10.A
 11.x≤且x≠-2
 12.a（m+n）（m-n）
 13.420
 14.360°
 15.4
 16.-1
 17.
 18.解：（1）原式=1-2×+3-1
=1-1+3-1
=2；

（2）原式=•
=•
=，
当x=时，原式=．
 19.20  36
 20.解：如图所示：

 21.（1）证明：∵∠BAC=∠DAF，
∴∠BAF=∠CAD，
在△BAF和△CAD中，
，
∴△BAF≌△CAD，
∴∠BFA=∠CDA=90°，
∵AF=AD，
∴∠AFD=∠ADF，
∵∠CDE+∠ADF=90°，∠BFE+∠AFD=90°，
∴∠BFE=∠CDE．

（2）解：作CN⊥DE于N，BM⊥DE于M．
∵△BAF≌△CAD，
∴BF=CD，
∵∠BFM=∠CDN，∠M=∠CND=90°，
∴△BFM≌△CDN，
∴BM=CN，
∵BM∥CN，
∴∠NCE=∠MBE，∵∠CEN=∠MEB，
∴△CNE≌△BME，
∴BE=CE，
在RtCDN中，CD=2，tan∠CDN=，
∴CN=4，DN=6，
∵DE=9，
∴EN=3，
∴EC===5，
∴BC=2EC=10．
 22.解：（1）当一个月内在本地通话200分钟时，
全球通需交费：50+0.4×200=130元，神州行需交费：0.6×200=120元；
当一个月内在本地通话300分钟时，
全球通需交费：50+0.4×300=170元，神州行需交费：0.6×300=180元；

（2）设一个月内在本地通话x分，
根据题意有：50+0.4x=0.6x，
解得：x=250，
即当本地通话时间为分钟时，两种计费方式的收费一样；

（3）由50+0.4x＞0.6x，
解得：x＜250
即当本地通话时间少于250分时，用神州行更合算；
由50+0.4x=0.6x，
解得：x=250，
即当本地通话时间等于250分时，用神州行和全球通没有区别，
由50+0.4x＜0.6x，
解得：x＞250
当本地通话时间多于250分时，用全球通更合算．
 23.解：过点D作DH⊥AC于点H，延长EB交AC于T，过点D作DG⊥EB交EB的延长线于点G，

在Rt△BCT中，BT=BCsin50°≈61.6（cm），
∵身高是170cm，坐垫高度为身高的0.6倍时，骑行者最舒适，
∴GE=1700.6=102（cm）,
∴GT=EG-ET=102-61.6-30=10.4（cm），
∵四边形DHTG是矩形，
∴DH=GT=10.4（cm），
在Rt△ADH中，AD==≈12.0（cm）
答：AD的长约为12.0cm．
 24.是  C，D
 25.解：（1）∵点A的坐标为（-1，0），对称轴为直线x=1，
∴，
解得：．
∴抛物线的解析式为：y=-x2+2x+3；

（2）∵当x=0时，y=3，
∴点C（0，3），
当y=0时，-x2+2x+3=0，
解得：x1=-1，x2=3，
∴点A（-1，0），点B（3，0），
设直线BC的解析式为：y=mx+n，
则，
解得：，
∴直线BC的解析式为：y=-x+3，
∴PF=（-m2+2m+3）-（-m+3）=-m2+3m；

（3）连接BF，延长FP交x轴于点H，
S△BCF=S△PCF+S△PBF=PF•OH+PF•BH=PF•（OH+BH）=PF•OB=（-m2+3m）=-（m-）2+，
则当m=时，△BCF的面积最大．