2020-2021学年6.2 指数函数教学ppt课件

这是一份2020-2021学年6.2 指数函数教学ppt课件，共26页。
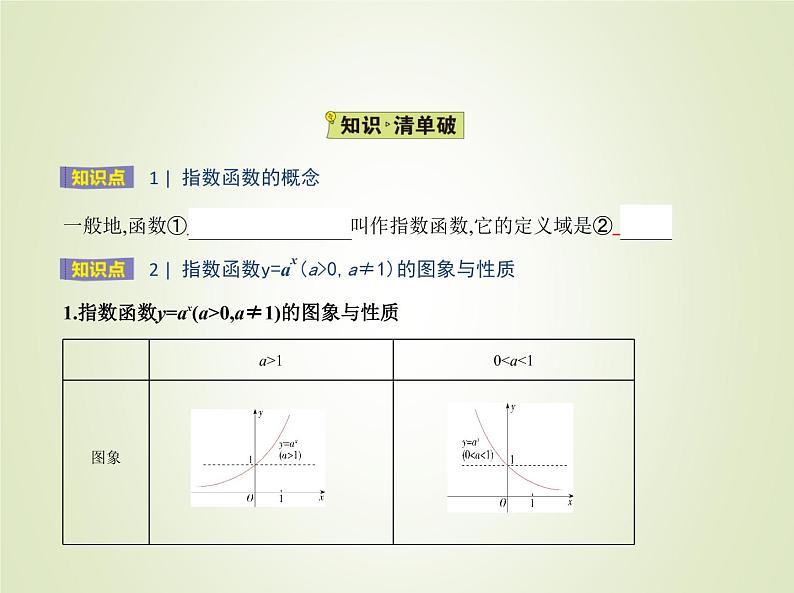
一般地,函数①    y=ax(a>0,a≠1)    叫作指数函数,它的定义域是②    R    .
1 | 指数函数的概念
2 | 指数函数y=ax(a>0,a≠1)的图象与性质
1.指数函数y=ax(a>0,a≠1)的图象与性质
2.常用结论(1)底数互为倒数的两个指数函数的图象关于y轴对称.(2)底数a对指数函数图象的影响.a与1的大小关系决定了图象的“升”与“降”.
(i)当a>1时,指数函数的图象从左到右是“上升”的,且当x>0时,底数a的值越大, 函数图象越“陡”,说明函数值增长得越快.(ii)当00时,ax>bx;当x0)个单位长度,得到⑧    y=ax+b    的图象; 把y=ax的图象向下平移b(b>0)个单位长度,得到y=ax-b的图象.简记为“左加右减,上加下减”.2.对称变换(a>0,a≠1)(1)函数y=ax的图象与y=a-x的图象关于y轴对称.(2)函数y=ax的图象与y=-ax的图象关于x轴对称.(3)函数y=ax的图象与y=-a-x的图象关于坐标原点对称.
3 | 指数函数图象的变换
1.函数y=2x-1是指数函数. (    ✕　)提示:形如y=ax(a>0,a≠1)的函数叫作指数函数,显然函数y=2x-1不是指数函数.2.函数y=a-x(a>0,a≠1)是R上的增函数. (    ✕　)提示:当00,a≠1)的定义域为[0,+∞). (　√　)提示:由题意得x≥0,故函数y= (a>0,a≠1)的定义域为[0,+∞).4.若指数函数f(x)=(2a+1)x在定义域上是增函数,则实数a的取值范围是(0,+∞). (　√　)提示:由题意可知2a+1>1,解得a>0.
判断正误，正确的画“ √” ，错误的画“ ✕” .
5.函数y=2x+1的图象可以由y=2x的图象向右平移1个单位长度得到. (    ✕　)提示:函数y=2x+1的图象可以由y=2x的图象向左平移1个单位长度得到.6.函数y=5x的图象与y=-5x的图象关于y轴对称.(    ✕　)提示:函数y=5x的图象与y=-5x的图象关于x轴对称.7.若f(x)是偶函数,当x>0时,f(x)=10x,则当x0,a≠1)的定义域是R,所以函数y=af(x)的定义域与f(x)的定 义域相同.(2)对于函数y=f(ax)(a>0,a≠1)的定义域,先令u=ax,然后确定y=f(u)的定义域,即u=ax 的值域,由此构造关于x的不等式(组),确定x的取值范围,得到y=f(ax)的定义域.2.求与指数函数有关的复合函数的值域时,重点是要注意指数函数的值域为(0,+∞).(1)求函数y=af(x)的值域,需先确定f(x)的值域,再根据指数函数y=ax的单调性确定函 数y=af(x)的值域;(2)求函数y=f(ax)的值域,先令u=ax,然后利用函数u=ax的单调性确定u=ax的值域,进
而确定函数y=f(u)的值域,即为y=f(ax)的值域.
求下列函数的定义域和值域:(1)y= ;(2)y=4x-2x+1;(3)y= (a>0,且a≠1).
思路点拨(1)利用根式的性质列不等式求函数的定义域,由x的范围得到 的范围,进而求出函数的值域;(2)根据指数函数的性质求函数的定义域,将y=4x-2x+1转化为关于2x的二次函数,进 而求出函数的值域;(3)根据分式的性质求函数的定义域,利用换元法或反解法求函数的值域.
解析    (1)由题意得1- ≥0,解得x≥0,∴函数的定义域为[0,+∞).∵x≥0,∴00,∴t+1>1,∴00,且a≠1) 的单调性求解;(3)形如ax>bx的不等式,可借助两函数y=ax,y=bx(a,b>0,且a,b≠1)的图象求解.
(1)设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是 (　C　)A.a