初中数学人教版九年级上册第二十三章 旋转综合与测试巩固练习

这是一份初中数学人教版九年级上册第二十三章 旋转综合与测试巩固练习，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
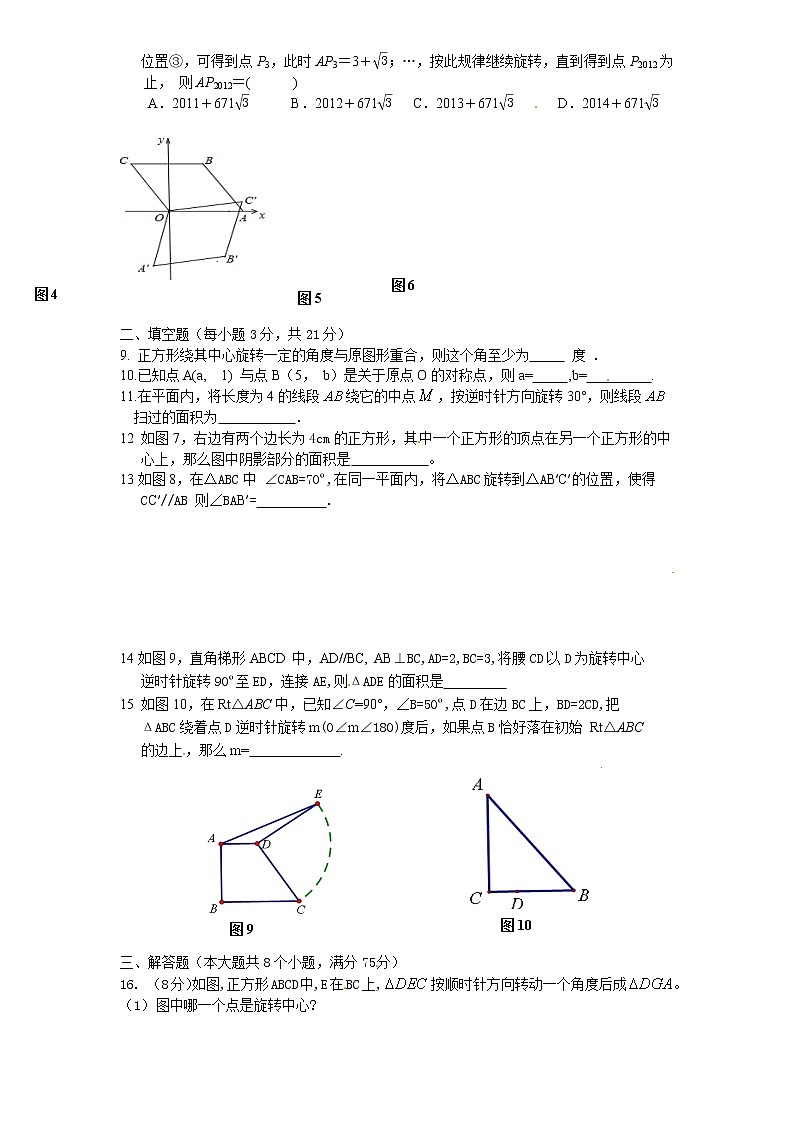
人教版九年级数学上册第23章《旋转》单元测试及答案 (3)一、选择题（每小题3分，共24分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内.1. 如下是一种电子计分牌呈现的数字图形，其中既是轴对称图形又是中心对称图形的是  （   ）A．     B．      C．     D．2、如图1，P是正△ABC内的一点，若将△PBC绕点B旋转到△P’BA，则∠PBP’的度    数是（    ）     A.45°       B.60°        C.90°      D.120°                3. 如图2，∠AOB＝90°，∠B＝30°，△A’OB’可以看作是由△AOB绕点O顺时针旋转   α角度得到的，若点A’在AB上，则旋转角α的大小可以是（    ）         A．30°  B．45°  C．60°  D．90°4 .如图3,在方格纸上建立的平面直角坐标系中，将△APO绕点O按顺时针方向旋转   90°，则旋转后点A的坐标为（    ）        A．（3，1）  B（3，2） C．（2，3） D．（1，3）   5. 已知点A的坐标为（a,  b),  O为坐标原点，连接OA, 将线段OA绕点O按逆时针  方向旋转90度得OA1 则点A1 的坐标为（   ）    A(－a,  b)  B（a,  －b)  C（－b,  a )    D（b,  －a ) 6、如图4是一个旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转   的度数至少为（     ）度.                                              A、30 o       B、45 o      C、60 o       D、90 o如图5，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B=120°，OA=2，将菱    形OABC绕原点顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（　　）   A．（，）　　B．（，）　　C．（1,   1）　　D．（，）8. 如图6，在△ABC中，∠ACB＝90º，∠B＝30º，AC＝1，AC在直线l上．将△ABC绕点 A   顺时针旋转到位置①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋   转到位置②，可得到点P2，此时AP2＝2＋；将位置②的三角形绕点P2顺时针旋转到   位置③，可得到点P3，此时AP3＝3＋；…，按此规律继续旋转，直到得到点P2012为止， 则AP2012＝(      )                                                   A．2011＋671      B．2012＋671   C．2013＋671      D．2014＋671  二、填空题（每小题3分，共21分）9. 正方形绕其中心旋转一定的角度与原图形重合，则这个角至少为      度 ．10.已知点A(a,  1) 与点B（5， b）是关于原点O的对称点，则a=     ,b=         .11.在平面内，将长度为4的线段绕它的中点，按逆时针方向旋转30°，则线段    扫过的面积为           ．12 如图7，右边有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中   心上，那么图中阴影部分的面积是           。13如图8，在ΔABC中 ∠CAB=70º,在同一平面内，将ΔABC旋转到ΔAB′C′的位置，使得    CC′//AB 则∠BAB′=          .                                                                                                                        14如图9，直角梯形ABCD中，AD//BC, AB⊥BC,AD=2,BC=3,将腰CD以D为旋转中心    逆时针旋转90º至ED，连接AE,则ΔADE的面积是         15 如图10，在Rt△ABC中，已知∠C=90°，∠B=50º,点D在边BC上，BD=2CD,把   ΔABC绕着点D逆时针旋转m(0∠m∠180)度后，如果点B恰好落在初始 Rt△ABC     的边上，那么m=             .                                                      三、解答题（本大题共8个小题，满分75分）16. （8分）如图,正方形ABCD中,E在BC上,按顺时针方向转动一个角度后成。（1） 图中哪一个点是旋转中心?（2） 旋转了多少度?（3） 求∠GDE的度数并指出△DGE的形状。                                                 17、（8分）如图，在直角三角形ABC中，，点D在BC的延长线上，且BD=AB，      过B作BEAC，与BD的垂线DE交于点E，（1）求证：（2）三角形BDE可由三角形ABC旋转得到，利用尺规作出旋转中心O（保留作图痕      迹，不写作法）             18 （9分）如图，在中，，，将绕点沿逆时           针方向旋转得到．（1）线段的长是               ，的度数是              ；（2）连结，求证：四边形是平行四边形；（3）求四边形的面积．          19（9分)如图，在ΔABC中，AB=AC,若将ΔABC绕点C顺时针180º得到ΔFEC。      （1）试猜想AE与BF有何关系，并说明理由；      （2）若ΔABC的面积为3cm2,求四边形ABFE的面积;       (3)当∠ACB为多少度时，四边形ABFE为矩形？说明理由。                                                                                           20.（9分）如图，在平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），       C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．  （1）请写出旋转中心的坐标是　   　，旋转角是　 度；  （2）以（1）中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°、180°的三角形；  （3）设Rt△ABC两直角边BC=a、AC=b、斜边AB=c，利用变换前后所形成的图案证明勾      股定理．                                                   21．（9分）如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于E，BF∥DE，交AG于F．（1）求证：AF﹣BF=EF；  （2）将△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为F′点，       若正方形边长为3，求点F′与旋转前的图中点E之间的距离．                                                                    22．（11分）一位同学拿了两块45º三角尺△MNK，△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC＝BC＝a．      （1）如图（1），两三角尺的重叠部分为，则重叠部分的面积为        ，       周长为        ．（2）将图（1）中的绕顶点逆时针旋转，得到图（2），此时重叠部分面      积为            ，周长为            ．（3）如果将绕旋转到不同于图（1）和图（2）的图形，如图（3），请你猜       想此时重叠部分的面积为多少？并试着加以验证．          23．（本题满分12分） （1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．       求证：CE＝CF；（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，       请你利用（1）的结论证明：GE＝BE＋GD．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB 上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．   答案  1——8 CBCDD CAB  9.  90       10.a=  -5   ,b=   -1       11.           12.    4cm2    13.  40º       14     1       15.  80º或120º (1) 点D  (2) 90º (3)∠GDE=90º △DGE是等腰直角三角形略18.（1）6，135°     （2）    ∴        又     ∴四边形是平行四边形     (3)  36   （1）AE=BF且AE//BF  （2）12cm2   （3） ∠ACB=60º（1）O（0，0）　，旋转角是　90º   （2）如图：               （3）有旋转的过程可知，四边形CC1C2C3和四边形AA1A2B是正方形． ∵S正方形CC1C2C3=S正方形AA1A2B+4S△ABC，∴（a+b）2=c2+4×ab，即a2+2ab+b2=c2+2ab，∴a2+b2=c2．（1）略      （2）根据题意知：∠FAF′=90°，DE=AF′=AF， ∴∠F′AE=∠AED=90°，即∠F′AE+∠AED=180°， ∴AF′∥ED，∴四边形AEDF′为平行四边形，又∠AED=90°， ∴四边形AEDF′是矩形，∴EF′=AD=3．22. 解：（1），(1＋)a；（2），2a；  （3）猜想：重叠部分的面积为。     理由如下：     过点M分别做AC、BC的垂线MH、MG，垂足为H、G。　     为说明方便，不妨设MN与AC的交点为E，MK与BC的交点为F。由于M是△ABC斜边AB的中点，AC＝BC＝a所以MH＝MG＝ 又因为 ∠HME＝∠GMF所以 Rt△MHE≌Rt△MGF 因此阴影部分的面积等于正方形CGMH的面积。而正方形CGMH的面积是MG·MH＝×＝23.（1）略       （2）证明： 如图2，延长AD至F，使DF=BE．连接CF．     由（1）知△CBE≌△CDF，∴∠BCE＝∠DCF．∴∠BCE＋∠ECD＝∠DCF＋∠ECD即∠ECF＝∠BCD＝90°，又∠GCE＝45°，∴∠GCF＝∠GCE＝45°．∵CE＝CF，∠GCE＝∠GCF，GC＝GC，∴△ECG≌△FCG．∴GE＝GF∴GE＝DF＋GD＝BE＋GD． （3）解：如图3，过C作CG⊥AD，交AD延长线于G．在直角梯形ABCD中，∵AD∥BC，∴∠A＝∠B＝90°，又∠CGA＝90°，AB＝BC，∴四边形ABCD 为正方形． ∴AG＝BC．已知∠DCE＝45°，根据（1）（2）可知，ED＝BE＋DG． 所以10=4+DG，即DG=6.设AB＝x，则AE＝x－4，AD＝x－6在Rt△AED中，   ∵，即．解这个方程，得：x＝12，或x＝－2（舍去）∴AB＝12． 所以梯形ABCD的面积为S=答：梯形ABCD的面积为108.