高中数学苏教版 (2019)必修 第一册7.3 三角函数的图象和性质示范课课件ppt

这是一份高中数学苏教版 (2019)必修 第一册7.3 三角函数的图象和性质示范课课件ppt，共23页。

一般地,函数y=sin(x+φ)(φ≠0)的图象可以看作是将函数y=sin x的图象上所有的点向①　左    (当φ>0时)或向右(当φ<0时)平移②　|φ|    个单位长度而得到的.
1 | φ(φ≠0)对函数y=sin(x+φ)的图象的影响
一般地,函数y=Asin x(A>0且A≠1)的图象,可以看作是将函数y=sin x的图象上所有点的纵坐标变为原来的③    A    倍(横坐标不变)而得到的.从而,函数y=Asin(ωx+φ)的值域是④　[-A,A]    ,即最大值是A,最小值是-A.
2 | A(A>0且A≠1)对y=Asin x的图象的影响
一般地,函数y=sin ωx(ω>0且ω≠1)的图象,可以看作是将函数y=sin x的图象上所有点的横坐标变为原来的⑤         倍(纵坐标⑥　不变    )而得到的.
3 | ω(ω>0且ω≠1)对函数y=sin ωx的图象的影响
一般地,函数y=sin(ωx+φ)(ω>0,φ≠0)的图象,可以看作是将函数y=sin ωx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移⑦         个单位长度而得到的.
4 | ω,φ(ω>0,φ≠0)对函数y=sin(ωx+φ)的图象的影响
5 | 函数y=sin x的图象与=Asin(ωx+φ)(A>0,ω>0)的图象的关系
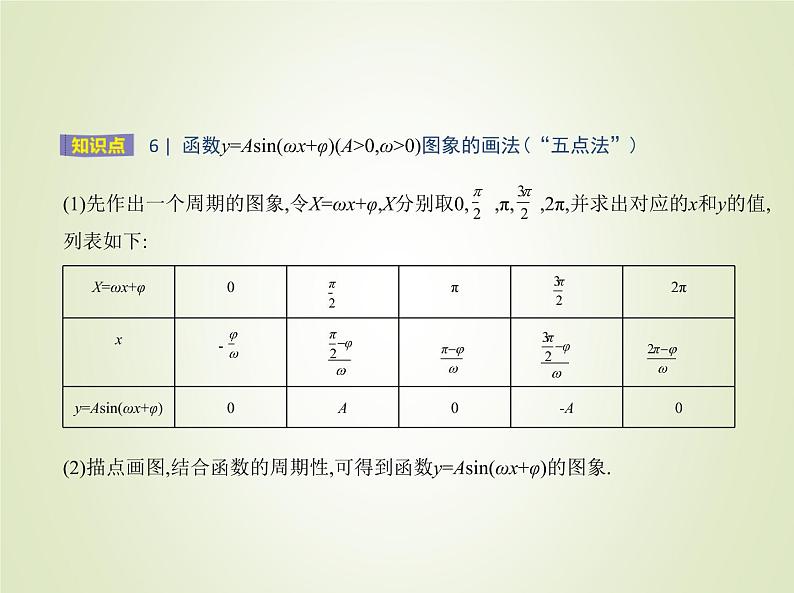
(1)先作出一个周期的图象,令X=ωx+φ,X分别取0, ,π, ,2π,并求出对应的x和y的值,列表如下:
6 | 函数y=Asin(ωx+φ)(A>0,ω>0)图象的画法(“五点法”)
(2)描点画图,结合函数的周期性,可得到函数y=Asin(ωx+φ)的图象.
1.将y=sin x的图象向左平移 个单位得到的图象所对应的函数是偶函数. (　√　)2.将y=sin 2x的图象向右平移 个单位得到的图象所对应的函数是y=sin . (    ✕　)提示:将y=sin 2x的图象向右平移 个单位得到的图象所对应的函数是y=sin .3.将y=cs 3x的图象向左平移 个单位得到的图象所对应的函数是y=cs . (　√　)
判断正误，正确的画“ √” ，错误的画“ ✕” .
4.函数y=sin 2x的图象是由y=sin x的图象上所有点的纵坐标保持不变,横坐标变为原来的2倍得到的. (    ✕　)提示:函数y=sin 2x的图象是由y=sin x的图象上所有点的纵坐标保持不变,横坐标 变为原来的 倍得到的.5.如果函数y=Acs(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心 之间的距离为 . (　√　)
由函数y=sin x的图象变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象有两种途径:①先平移后伸缩;②先伸缩后平移.具体过程如下:方法1:y=sin x的图象 y=sin(x+φ)的图象 y=sin(ωx+φ)的图象 
1 | 函数图象的变换
y=Asin(ωx+φ)的图象.方法2:y=sin x的图象  y=sin ωx的图象 y=sin(ωx+φ)的图象 y=Asin(ωx+φ)的图象.
值得注意的是,在变换过程中横向的伸缩和左右平移仅针对x而言,如果x前面有系数ω,需要把系数ω提出来,再进行变换.
函数y= sin + 的图象可由y=sin x的图象经过怎样的变换得到?
思路点拨思路一:先平移变换,再伸缩变换;思路二:先伸缩变换,再平移变换.
解析    解法一:把函数y=sin x的图象向左平移 个单位长度,得到函数y=sin的图象;把得到的函数图象上各点的横坐标变为原来的 倍(纵坐标不变),得到函数y=sin 的图象;把得到的函数图象上各点的纵坐标变为原来的 倍(横坐标不变),得到函数y=  sin 的图象;把得到的函数图象向上平移 个单位长度,得到函数y= sin + 的图象.解法二:把函数y=sin x的图象上各点的横坐标变为原来的 倍(纵坐标不变),得到函数y=sin 2x的图象;
把得到的函数图象向左平移 个单位长度,得到函数y=sin 的图象;把得到的函数图象上各点的纵坐标变为原来的 倍(横坐标不变),得到函数y=  sin 的图象;把得到的函数图象向上平移 个单位长度,得到函数y= sin + 的图象.
名师点睛    对于函数y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0),其图象的基本变换有 如下几种:(1)纵向伸缩变换:由A的变化引起的,A>1时伸长,A<1时缩短.(2)横向伸缩变换:由ω的变化引起的,ω>1时缩短,ω<1时伸长.(3)横向平移变换:由φ的变化引起的,φ>0时左移,φ<0时右移.(4)纵向平移变换:由k的变化引起的,k>0时上移,k<0时下移.
2 | 根据图象求函数的解析式
由图象确定函数解析式的方法1.逐一定参法(1)由函数图象上的最高点、最低点来确定A.(2)由函数图象与x轴的交点确定T,由T= 确定ω.(3)确定函数y=Asin(ωx+φ)中φ的值.其方法有两种:①代入法:把图象上的一个已知点的坐标代入y=Asin(ωx+φ)(此时A与ω已知),求得φ.②五点对应法:确定φ值时,往往以“五点法”中的点 为突破口.
2.待定系数法将若干特殊点代入函数解析式,可以求得相关待定系数A,ω,φ.这里需要注意的是,要认清所选择的点属于五个点中的哪一个点,并能正确代入函数解析式.3.图象变换法运用逆向思维,先确定y=Asin ωx,再根据图象平移规律确定相关的参数.
如图是函数y=Asin(ωx+φ) A>0,ω>0,|φ|<  的图象的一部分,求此函数的解析式. 
解析    解法一(逐一定参法):由题图知A=3,T= - =π,∴ω= =2,∴y=3sin(2x+φ).∵点 在函数图象上,∴0=3sin ,∴- ×2+φ=kπ(k∈Z),得φ= +kπ(k∈Z).∵|φ|< ,∴φ= .∴y=3sin  .
解法二(待定系数法):由题图知A=3.∵图象过点 和 ,∴ 解得 ∴y=3sin .解法三(图象变换法):由题图知A=3,T= - =π,点 在函数图象上,
∴函数图象是由y=3sin 2x的图象向左平移 个单位长度得到的,∴y=3sin ,即y=3sin  .
3|函数y=Asin(ωx+φ)的性质
1.函数y=Asin(ωx+φ)的最小正周期T= .2.判断函数y=Asin(ωx+φ)(A,ω≠0)是否具有奇偶性,关键是看它能否转化为y=Asinωx(A,ω≠0)或y=Acs ωx(A,ω≠0)的形式.3.求y=Asin(ωx+φ)(A>0,ω≠0)的单调区间,一般将ωx+φ看成一个整体,代入y=sin x的单调区间对应的不等式,解x即可.要注意ω的正负对单调区间的影响.4.讨论y=Asin(ωx+φ)(A>0,ω≠0)图象的对称性,一般将ωx+φ看成一个整体,令ωx+φ=kπ+ (k∈Z),可求出函数图象的对称轴;令ωx+φ=kπ(k∈Z),可求出函数图象的对称中心的横坐标.这里要注意以下几个隐含条件:(1)两条相邻对称轴之间的距离为 个周期;
(2)函数在对称轴处取得最大值或最小值;(3)两个相邻最大值之间为一个周期,两个相邻最小值之间为一个周期,两个相邻 最值之间为 个周期.
已知函数f(x)=2sin (ω>0,0<φ<π)为奇函数,且f(x)图象的相邻两条对称轴间的距离为 .(1)当x∈ 时,求f(x)的单调递减区间;(2)将函数f(x)的图象向右平移 个单位长度,再把横坐标缩小为原来的 倍(纵坐标不变),得到函数y=g(x)的图象,当x∈ 时,求函数g(x)的值域.
解析    (1)因为函数f(x)图象的相邻两条对称轴间的距离为 ,所以最小正周期T=π,所以ω=2.因为函数f(x)为奇函数,所以f(0)=2sin =0,所以φ- =kπ,k∈Z.因为0<φ<π,所以φ= .所以f(x)=2sin 2x.令 +2kπ≤2x≤ +2kπ,k∈Z,解得 +kπ≤x≤ +kπ,k∈Z,所以函数f(x)的单调递减区间为 ,k∈Z.