2021学年8.5 乘法公式教学设计

这是一份2021学年8.5 乘法公式教学设计，共7页。教案主要包含了学生学情分析，教学目标等内容，欢迎下载使用。


二、学生学情分析
学生的技能基础：学生通过对本章前几节课的学习，已经学习了整式的概念、整式的加减、幂的运算、整式的乘法、平方差公式，这些基础知识的学习为本节课的学习奠定了基础．
学生活动经验基础：在平方差公式一节的学习中，学生已经经历了探索和应用的过程，获得了一些数学活动的经验，培养了一定的符号感和推理能力；同时在相关知识的学习过程中，学生经历了很多探究学习的过程，具有了一定的独立探究意识以及与同伴合作交流的能力．
三、教学目标
知识与技能：
（1）让学生会推导完全平方公式，并能进行简单的应用．
（2）了解完全平方公式的几何背景．
过程与方法：
（1）由学生经历探索完全平方公式的过程，进一步发展学生的符号感与推理能力．
（2）发展学生的数形结合的数学思想．
情感态度价值观
让学生经历“特殊到一般再到特殊”（即：特例─归纳─猜想─验证─用数学符号表示—解决问题）这一数学活动过程，积累数学活动的经验，体会数学的简洁美和数形结合的思想方法．培养他们合情推理和归纳的能力以及在解决问题过程中与他人合作交流的意识．
重难点
1.理解并掌握完全平方公式的推导过程、结构特点、几何解释并能够灵活应用.（重点）
2.理解完全平方公式的结构特征，灵活应用完全平方公式.（难点）
四．教学过程
情境引入
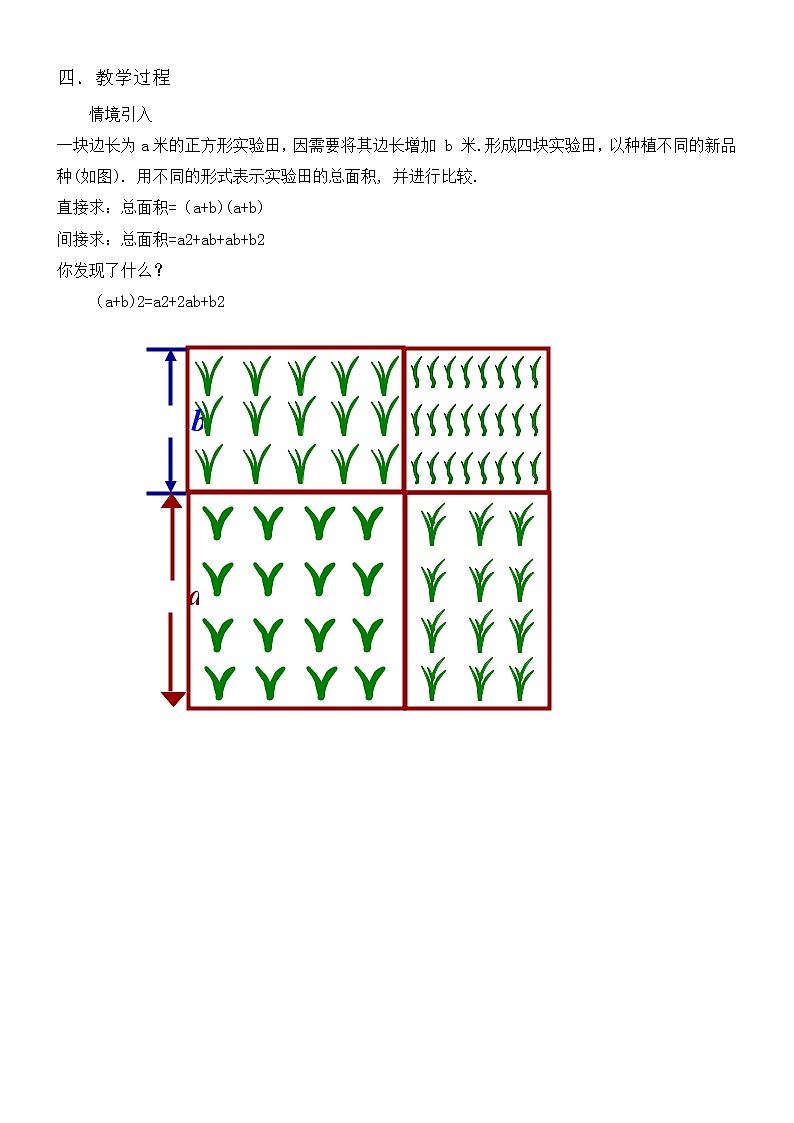
一块边长为a米的正方形实验田，因需要将其边长增加 b 米.形成四块实验田，以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
直接求：总面积=（a+b)(a+b)
间接求：总面积=a2+ab+ab+b2
你发现了什么？
（a+b)2=a2+2ab+b2
b
a
合作探究公式的运用
计算下列多项式的积，你能发现什么规律？
1) (p+1)2=(p+1)(p+1)= .
(2) (m+2)2=(m+2)(m+2)=
(3) (p-1)2=(p-1)(p-1)=
(4) (m-2)2=(m-2)(m-2)=
根据上面的规律，你能直接下面式子的写出答案吗？完全平方公式.
知识要点
简记为：“首平方，尾平方，积的2倍中间放”
两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.这两个等式分别叫作两数和、两数差的完全平方公式.
公式特征：1.积为二次三项式；
积中两项为两数的平方和；
另一项是两数积的2倍，且与乘式中间的符号相同.
4.公式中的字母a，b可以表示数，单项式和多项式.
练一练
已知x2＋16x＋k是完全平方式，则常数k等于( )
A.64 B.48 C.32 D.16
变式题：已知x2＋kx＋25是完全平方式，则常数k=_____
观察与思考
你能根据图1和图2中的面积说明完全平方公式吗?
b
a
a
b
b
a
b
a
图 1
图2
例3 运用乘法公式计算:
(1) (a+b+c)2
解：(1)原式 = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2bc+2ac；把其中两项看成一个整体，再按照完全平方公式进行计算五.当堂练习
1．在等号右边的括号内填上适当的项：
（1）a+b-c=a+（ ）
（2）a-b+c=a-（ ）
（3）a-b-c=a-（ ）能否用去括号法则检查添括号是否正确?
2．判断下列运算是否正确．
（1）2a-b-c=2a-（b-c）
（2）m-3n+2a-b=m+（3n+2a-b）
（3）2x-3y+2=-（2x+3y-2）
a-2b-4c+5=（a-2b）-（4c-5）
（4）a+b+c=a-（ ）
4.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
5.已知x+y=8,x-y=4,求xy.
解题时常用结论：
a2+b2=(a+b)2-2ab=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.
六.课堂小结
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子，可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同（从公式结构特点及结果两方面）
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
七.学生反思
活动内容：通过今天这堂课的学习，你有哪些收获？
收获1：认识了完全平方公式，并能简单应用；
收获2：了解了两数和与两数差的完全平方公式之间的差异；
收获3：感受到数形结合的数学思想在数学中的作用．
活动目的：通过对一堂课的归纳与总结，巩固学生对完全平方公式的认识，体会数学思想的精妙．
板书设计

九.作业布置
《轻松学数学》填空，选择b
a
a
b
b
a
b
a
图 1
图2