数学八年级下册18.2.2 菱形学案

科目

数学

课题

矩形的判定

学     习    目    标

1．理解并把握矩形的判定定理，能有理有据的推理证明，精练精确     地书写表达。

2. 能娴熟应用矩形的性质、判定等学问进行有关证明和计算.

重点

把握并会运用矩形的判定

难点

运用矩形的判定进行简洁的推理与计算。

学法指导及使用说明：用15分钟的时间，结合课本完成一、二部分，用25分钟完成三、四部分。

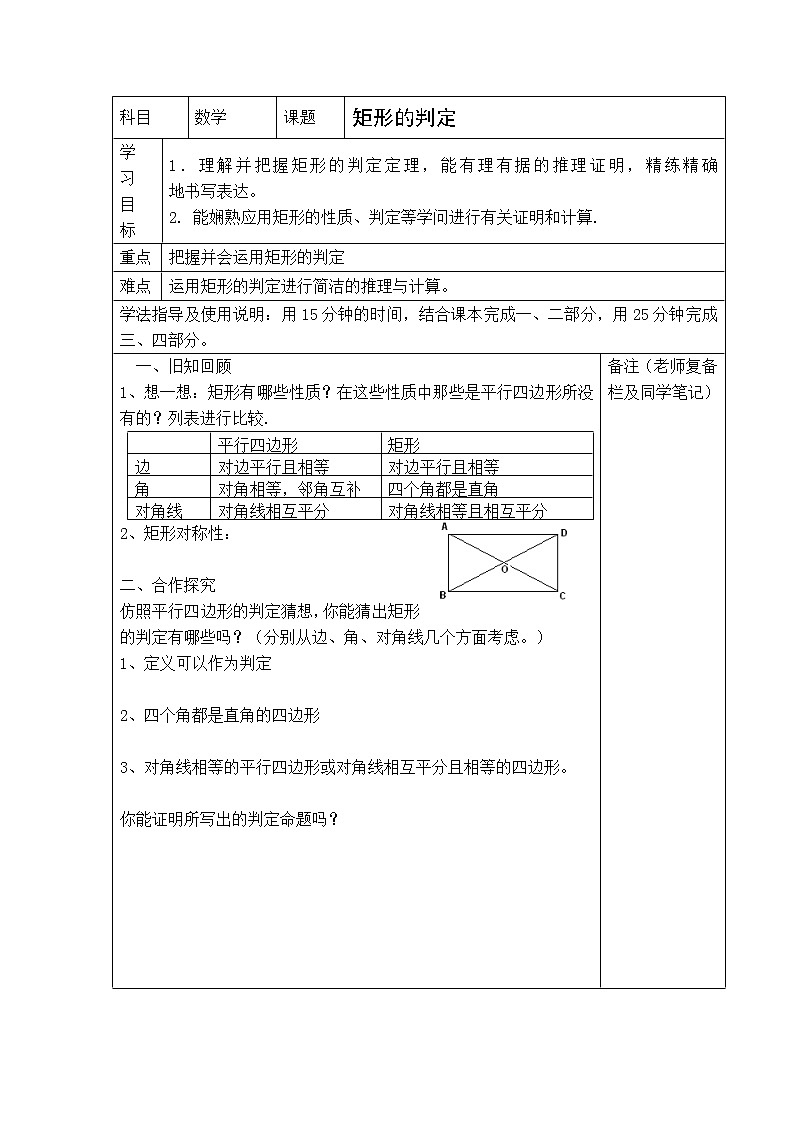
　一、旧知回顾

1、想一想：矩形有哪些性质？在这些性质中那些是平行四边形所没有的？列表进行比较.

2、矩形对称性：

二、合作探究

仿照平行四边形的判定猜想，你能猜出矩形的判定有哪些吗？（分别从边、角、对角线几个方面考虑。）

1、定义可以作为判定

2、四个角都是直角的四边形

3、对角线相等的平行四边形或对角线相互平分且相等的四边形。

你能证明所写出的判定命题吗？

备注（老师复备栏及同学笔记）

三、应用

例1. 如图，□ ABCD的对角线AC、BD交于点O，△AOB是正三角形，AB=4cm.

(1) 求证□ ABCD是矩形.

(2) 求□ ABCD的面积.

2．已知：如图 ，在△ABC中，∠C＝90°， CD为中线，延长CD到点E，使得 DE＝CD．连结AE，BE，则四边形ACBE为矩形吗？说明理由。

答案：四边形ACBE是矩形.由于CD是Rt△ACB斜边上的中线，

      所以DA=DC=DB,又由于DE=CD，所以DA=DC=DB=DE,所以四边形ABCD是矩形（对角线相等且相互平分的四边形是矩形）。

四、课堂检测：

1．下列说法正确的是（   ）

A.有一组对角是直角的四边形肯定是矩形  

B.有一组邻角是直角的四边形肯定是矩形

C.对角线相互平分的四边形是矩形        

D.对角互补的平行四边形是矩形

2. 矩形各角平分线围成的四边形是（   ）

 A.平行四边形       B.矩形        C.菱形     D.正方形

3. 下列判定矩形的说法是否正确

  （1）有一个角是直角的四边形是矩形         （    ）

  （2）四个角都是直角的四边形是矩形         （    ）

（3）四个角都相等的四边形是矩形           （    ）

（4）对角线相等的四边形是矩形             （    ）

（5）对角线相等且相互垂直的四边形是矩形   （    ）

（6）对角线相等且相互平分的四边形是矩形   （    ）

4. （2011江苏淮安）在四边形ABCD中，AB=DC，AD=BC.请再添加一个条件，使四边形ABCD是矩形.你添加的条件是          .(写出一种即可)

五、我的收获：

六、课后作业：

备注（老师复备栏及同学笔记）