江苏省南京市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案）

这是一份江苏省南京市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案），共14页。

江苏省南京市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案）

一．正数和负数（共1小题）
1．（2021•南京）北京与莫斯科的时差为5小时，例如，北京时间13：00，她们相约在各自当地时间9：00～17：00之间选择一个时刻开始通话，这个时刻可以是北京时间（　　）
A．10：00 B．12：00 C．15：00 D．18：00
二．有理数的减法（共1小题）
2．（2020•南京）计算3﹣（﹣2）的结果是（　　）
A．﹣5 B．﹣1 C．1 D．5
三．有理数的混合运算（共1小题）
3．（2017•南京）计算12+（﹣18）÷（﹣6）﹣（﹣3）×2的结果是（　　）
A．7 B．8 C．21 D．36
四．科学记数法—表示较大的数（共2小题）
4．（2021•南京）截至2021年6月8日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗超过800000000剂次．用科学记数法表示800000000是（　　）
A．8×108 B．0.8×109 C．8×109 D．0.8×1010
5．（2019•南京）2018年中国与“一带一路”沿线国家货物贸易进出口总额达到13000亿美元．用科学记数法表示13000是（　　）
A．0.13×105 B．1.3×104 C．13×103 D．130×102
五．平方根（共1小题）
6．（2020•南京）3的平方根是（　　）
A．9 B． C．﹣ D．±
六．算术平方根（共2小题）
7．（2018•南京）的值等于（　　）
A． B．﹣ C．± D．
8．（2017•南京）若方程（x﹣5）2＝19的两根为a和b，且a＞b，则下列结论中正确的是（　　）
A．a是19的算术平方根 B．b是19的平方根
C．a﹣5是19的算术平方根 D．b+5是19的平方根
七．立方根（共1小题）
9．（2019•南京）面积为4的正方形的边长是（　　）
A．4的平方根 B．4的算术平方根
C．4开平方的结果 D．4的立方根
八．实数与数轴（共1小题）
10．（2019•南京）实数a、b、c满足a＞b且ac＜bc，它们在数轴上的对应点的位置可以是（　　）
A． B．
C． D．
九．估算无理数的大小（共3小题）
11．（2019•南京）下列整数中，与10﹣最接近的是（　　）
A．4 B．5 C．6 D．7
12．（2018•南京）下列无理数中，与4最接近的是（　　）
A． B． C． D．
13．（2017•南京）若＜a＜，则下列结论中正确的是（　　）
A．1＜a＜3 B．1＜a＜4 C．2＜a＜3 D．2＜a＜4
一十．分数指数幂（共1小题）
14．（2021•南京）一般地，如果xn＝a（n为正整数，且n＞1），那么x叫做a的n次方根．下列结论中正确的是（　　）
A．16的4次方根是2
B．32的5次方根是±2
C．当n为奇数时，2的n次方根随n的增大而减小
D．当n为奇数时，2的n次方根随n的增大而增大
一十一．幂的乘方与积的乘方（共3小题）
15．（2021•南京）计算（a2）3•a﹣3的结果是（　　）
A．a2 B．a3 C．a5 D．a9
16．（2019•南京）计算（a2b）3的结果是（　　）
A．a2b3 B．a5b3 C．a6b D．a6b3
17．（2018•南京）计算a3•（a3）2的结果是（　　）
A．a8 B．a9 C．a11 D．a18
一十二．同底数幂的除法（共2小题）
18．（2020•南京）计算（a3）2÷a2的结果是（　　）
A．a3 B．a4 C．a7 D．a8
19．（2017•南京）计算106×（102）3÷104的结果是（　　）
A．103 B．107 C．108 D．109
一十三．根与系数的关系（共1小题）
20．（2020•南京）关于x的方程（x﹣1）（x+2）＝p2（p为常数）的根的情况，下列结论中正确的是（　　）
A．两个正根 B．两个负根
C．一个正根，一个负根 D．无实数根
一十四．坐标与图形性质（共1小题）
21．（2017•南京）过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（　　）
A．（4，） B．（4，3） C．（5，） D．（5，3）
一十五．认识立体图形（共1小题）
22．（2017•南京）不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征．甲同学：它有4个面是三角形；乙同学：它有8条棱．该模型的形状对应的立体图形可能是（　　）
A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
一十六．截一个几何体（共1小题）
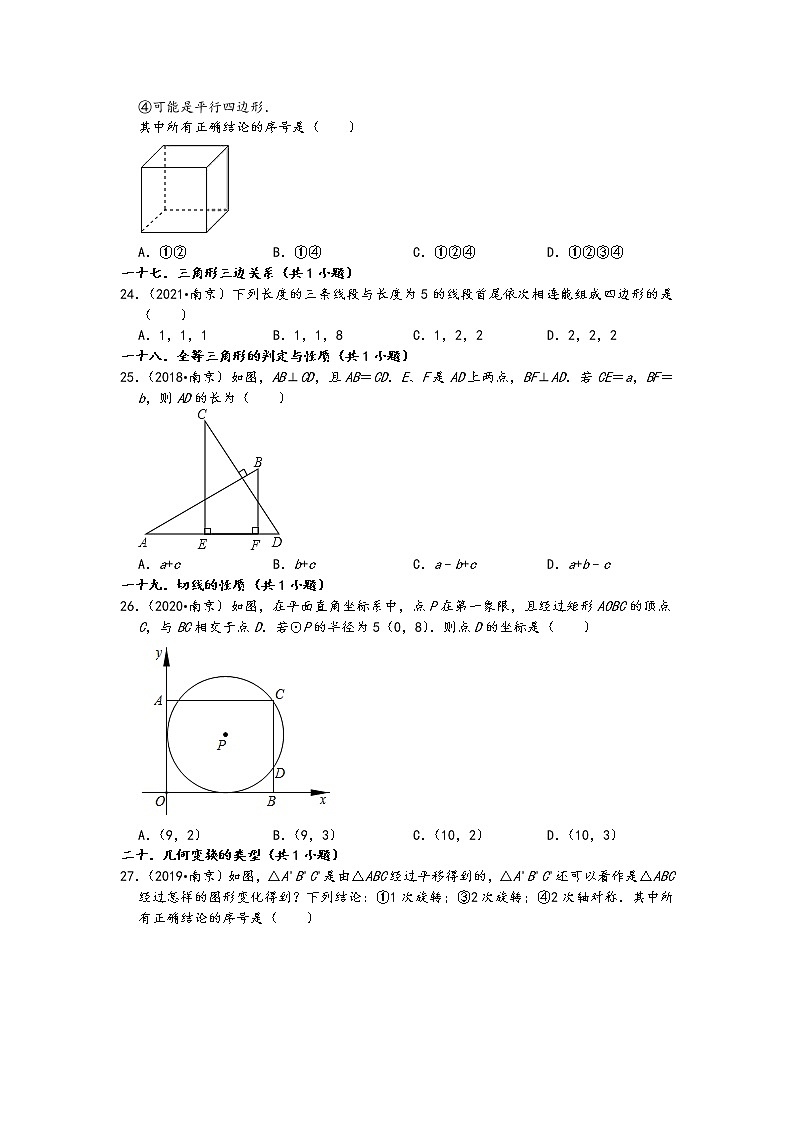
23．（2018•南京）用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：
①可能是锐角三角形；
②可能是直角三角形；
③可能是钝角三角形；
④可能是平行四边形．
其中所有正确结论的序号是（　　）

A．①② B．①④ C．①②④ D．①②③④
一十七．三角形三边关系（共1小题）
24．（2021•南京）下列长度的三条线段与长度为5的线段首尾依次相连能组成四边形的是（　　）
A．1，1，1 B．1，1，8 C．1，2，2 D．2，2，2
一十八．全等三角形的判定与性质（共1小题）
25．（2018•南京）如图，AB⊥CD，且AB＝CD．E、F是AD上两点，BF⊥AD．若CE＝a，BF＝b，则AD的长为（　　）

A．a+c B．b+c C．a﹣b+c D．a+b﹣c
一十九．切线的性质（共1小题）
26．（2020•南京）如图，在平面直角坐标系中，点P在第一象限，且经过矩形AOBC的顶点C，与BC相交于点D．若⊙P的半径为5（0，8）．则点D的坐标是（　　）

A．（9，2） B．（9，3） C．（10，2） D．（10，3）
二十．几何变换的类型（共1小题）
27．（2019•南京）如图，△A'B'C'是由△ABC经过平移得到的，△A'B'C'还可以看作是△ABC经过怎样的图形变化得到？下列结论：①1次旋转；③2次旋转；④2次轴对称．其中所有正确结论的序号是（　　）

A．①④ B．②③ C．②④ D．③④
二十一．中心投影（共1小题）
28．（2021•南京）如图，正方形纸板的一条对角线垂直于地面，纸板上方的灯（看作一个点），正方形纸板在地面上形成的影子的形状可以是（　　）

A． B． C． D．
二十二．条形统计图（共1小题）
29．（2020•南京）党的十八大以来，党中央把脱贫攻坚摆到更加突出的位置．根据国家统计局发布的数据，2012～2019年年末全国农村贫困人口的情况如图所示．

根据图中提供的信息，下列说法错误的是（　　）
A．2019年末，农村贫困人口比上年末减少551万人
B．2012年末至2019年末，农村贫困人口累计减少超过9000万人
C．2012年末至2019年末，连续7年每年农村贫困人口减少1000万人以上
D．为在2020年末农村贫困人口全部脱贫，今年要确保完成减少551万农村贫困人口的任务
二十三．方差（共1小题）
30．（2018•南京）某排球队6名场上队员的身高（单位：cm）是：180，184，190，192，与换人前相比，场上队员的身高（　　）
A．平均数变小，方差变小 B．平均数变小，方差变大
C．平均数变大，方差变小 D．平均数变大，方差变大

参考答案与试题解析
一．正数和负数（共1小题）
1．（2021•南京）北京与莫斯科的时差为5小时，例如，北京时间13：00，她们相约在各自当地时间9：00～17：00之间选择一个时刻开始通话，这个时刻可以是北京时间（　　）
A．10：00 B．12：00 C．15：00 D．18：00
【详解】解：由题意得，北京时间应该比莫斯科时间早5小时，
当莫斯科时间为9：00，则北京时间为14：00，则莫斯科时间为12：00；
所以这个时刻可以是14：00到17：00之间，
所以这个时刻可以是北京时间15：00．
【答案】C．
二．有理数的减法（共1小题）
2．（2020•南京）计算3﹣（﹣2）的结果是（　　）
A．﹣5 B．﹣1 C．1 D．5
【详解】解：3﹣（﹣2）＝2+2＝5．
【答案】D．
三．有理数的混合运算（共1小题）
3．（2017•南京）计算12+（﹣18）÷（﹣6）﹣（﹣3）×2的结果是（　　）
A．7 B．8 C．21 D．36
【详解】解：原式＝12+3+6＝21，
【答案】C．
四．科学记数法—表示较大的数（共2小题）
4．（2021•南京）截至2021年6月8日，31个省（自治区、直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗超过800000000剂次．用科学记数法表示800000000是（　　）
A．8×108 B．0.8×109 C．8×109 D．0.8×1010
【详解】解：将800000000用科学记数法表示为：8×108．
【答案】A．
5．（2019•南京）2018年中国与“一带一路”沿线国家货物贸易进出口总额达到13000亿美元．用科学记数法表示13000是（　　）
A．0.13×105 B．1.3×104 C．13×103 D．130×102
【详解】解：13000＝1.3×106，
【答案】B．
五．平方根（共1小题）
6．（2020•南京）3的平方根是（　　）
A．9 B． C．﹣ D．±
【详解】解：∵（）2＝8，
∴3的平方根．
【答案】D．
六．算术平方根（共2小题）
7．（2018•南京）的值等于（　　）
A． B．﹣ C．± D．
【详解】解：，
【答案】A．
8．（2017•南京）若方程（x﹣5）2＝19的两根为a和b，且a＞b，则下列结论中正确的是（　　）
A．a是19的算术平方根 B．b是19的平方根
C．a﹣5是19的算术平方根 D．b+5是19的平方根
【详解】解：∵方程（x﹣5）2＝19的两根为a和b，
∴a﹣6和b﹣5是19的两个平方根，且互为相反数，
∵a＞b，
∴a﹣5是19的算术平方根，
【答案】C．
七．立方根（共1小题）
9．（2019•南京）面积为4的正方形的边长是（　　）
A．4的平方根 B．4的算术平方根
C．4开平方的结果 D．4的立方根
【详解】解：面积为4的正方形的边长是，即为3的算术平方根；
【答案】B．
八．实数与数轴（共1小题）
10．（2019•南京）实数a、b、c满足a＞b且ac＜bc，它们在数轴上的对应点的位置可以是（　　）
A． B．
C． D．
【详解】解：因为a＞b且ac＜bc，
所以c＜0．
选项A符合a＞b，c＜0条件．
选项B不满足a＞b，选项C，故满足条件的对应点位置不可以是B、C、D．
【答案】A．
九．估算无理数的大小（共3小题）
11．（2019•南京）下列整数中，与10﹣最接近的是（　　）
A．4 B．5 C．6 D．7
【详解】解：解法一：∵9＜13＜16，
∴3＜＜3，
∵3.62＝12.96，3.75＝13.69，
∴3.6＜＜5.7，
∴﹣3.5＜﹣＜﹣3.6，
∴10﹣4.7＜10﹣＜10﹣3.4，
∴6.3＜10﹣＜6.4，
∴与10﹣最接近的是6．
解法二：∵8＜＜4，
∴6＜10﹣＜6，
∵3.55＝12.25，且12.25＜13，
∴＞3.5，
∴10﹣＜3.5，
∴与10﹣最接近的是6．
【答案】C．
12．（2018•南京）下列无理数中，与4最接近的是（　　）
A． B． C． D．
【详解】解：∵＝4，
∴与4最接近的无理数是：．
【答案】C．
13．（2017•南京）若＜a＜，则下列结论中正确的是（　　）
A．1＜a＜3 B．1＜a＜4 C．2＜a＜3 D．2＜a＜4
【详解】解：∵1＜6，3，
又∵＜a＜，
∴4＜a＜4，
【答案】B．
一十．分数指数幂（共1小题）
14．（2021•南京）一般地，如果xn＝a（n为正整数，且n＞1），那么x叫做a的n次方根．下列结论中正确的是（　　）
A．16的4次方根是2
B．32的5次方根是±2
C．当n为奇数时，2的n次方根随n的增大而减小
D．当n为奇数时，2的n次方根随n的增大而增大
【详解】解：A、∵（±2）4＝16，
∴16的6次方根是±2，故A不正确；
B、32的5次方根是5；
C、设x＝，则x15＝27＝32，y15＝23＝2，
∵x15＞y15且x＞1，y＞1，
∴x＞y，
∴当n为奇数时，2的n次方根随n的增大而减小；
D、当n为奇数时，故D不选项正确；
【答案】C．
一十一．幂的乘方与积的乘方（共3小题）
15．（2021•南京）计算（a2）3•a﹣3的结果是（　　）
A．a2 B．a3 C．a5 D．a9
【详解】解：（a2）3•a﹣8＝a6•a﹣3＝a5﹣3＝a3．
【答案】B．
16．（2019•南京）计算（a2b）3的结果是（　　）
A．a2b3 B．a5b3 C．a6b D．a6b3
【详解】解：（a2b）3＝（a2）3b3＝a6b3．
【答案】D．
17．（2018•南京）计算a3•（a3）2的结果是（　　）
A．a8 B．a9 C．a11 D．a18
【详解】解：a3•（a3）2＝a9，
【答案】B．
一十二．同底数幂的除法（共2小题）
18．（2020•南京）计算（a3）2÷a2的结果是（　　）
A．a3 B．a4 C．a7 D．a8
【详解】解：（a3）2÷a7＝a3×2÷a2＝a6﹣2＝a5，
【答案】B．
19．（2017•南京）计算106×（102）3÷104的结果是（　　）
A．103 B．107 C．108 D．109
【详解】解：106×（102）5÷104
＝106×103÷104
＝106+3﹣4
＝108．
【答案】C．
一十三．根与系数的关系（共1小题）
20．（2020•南京）关于x的方程（x﹣1）（x+2）＝p2（p为常数）的根的情况，下列结论中正确的是（　　）
A．两个正根 B．两个负根
C．一个正根，一个负根 D．无实数根
【详解】解：∵关于x的方程（x﹣1）（x+2）＝p6（p为常数），
∴x2+x﹣2﹣p3＝0，
∴b2﹣5ac＝1+8+3p2＝9+4p2＞0，
∴方程有两个不相等的实数根，
根据根与系数的关系，方程的两个根的积为﹣6﹣p2＜0，
∴一个正根，一个负根，
【答案】C．
一十四．坐标与图形性质（共1小题）
21．（2017•南京）过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（　　）
A．（4，） B．（4，3） C．（5，） D．（5，3）
【详解】解：如图，设△ABC的外心E（4，则CE＝5﹣t，
∵EC＝AE，
∴3﹣t＝，
解得t＝，可得结论．
【答案】A．

一十五．认识立体图形（共1小题）
22．（2017•南京）不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征．甲同学：它有4个面是三角形；乙同学：它有8条棱．该模型的形状对应的立体图形可能是（　　）
A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
【详解】解：四棱锥的底面是四边形，侧面是四个三角形，
底面有四条棱，侧面有4条棱，
【答案】D．
一十六．截一个几何体（共1小题）
23．（2018•南京）用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：
①可能是锐角三角形；
②可能是直角三角形；
③可能是钝角三角形；
④可能是平行四边形．
其中所有正确结论的序号是（　　）

A．①② B．①④ C．①②④ D．①②③④
【详解】解：用平面去截正方体，得的截面可能为三角形、五边形，而三角形只能是锐角三角形．
【答案】B．
一十七．三角形三边关系（共1小题）
24．（2021•南京）下列长度的三条线段与长度为5的线段首尾依次相连能组成四边形的是（　　）
A．1，1，1 B．1，1，8 C．1，2，2 D．2，2，2
【详解】解：A、∵1+1+3＝3＜5，
∴此三条线段与长度为3的线段不能组成四边形，故不符合题意；
B、∵1+1+2＝7＜8，
∴此三条线段与长度为3的线段不能组成四边形，故不符合题意；
C、∵1+2+8＝5，
∴此三条线段与长度为5的线段不能组成四边形，故不符合题意；
D、∵4+2+2＝2＞5，
∴此三条线段与长度为5的线段能组成四边形，故符合题意；
【答案】D．
一十八．全等三角形的判定与性质（共1小题）
25．（2018•南京）如图，AB⊥CD，且AB＝CD．E、F是AD上两点，BF⊥AD．若CE＝a，BF＝b，则AD的长为（　　）

A．a+c B．b+c C．a﹣b+c D．a+b﹣c
【详解】解：∵AB⊥CD，CE⊥AD，
∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，
∴∠A＝∠C，∵AB＝CD，
∴△ABF≌△CDE，
∴AF＝CE＝a，BF＝DE＝b，
∵EF＝c，
∴AD＝AF+DF＝a+（b﹣c）＝a+b﹣c，
【答案】D．
一十九．切线的性质（共1小题）
26．（2020•南京）如图，在平面直角坐标系中，点P在第一象限，且经过矩形AOBC的顶点C，与BC相交于点D．若⊙P的半径为5（0，8）．则点D的坐标是（　　）

A．（9，2） B．（9，3） C．（10，2） D．（10，3）
【详解】解：设⊙O与x、y轴相切的切点分别是F，连接PE、PD，
则PE⊥y轴，PF⊥x轴，
∵∠EOF＝90°，
∴四边形PEOF是矩形，
∵PE＝PF，PE∥OF，
∴四边形PEOF为正方形，
∴OE＝PF＝PE＝OF＝5，
∵A（0，4），
∴OA＝8，
∴AE＝8﹣2＝3，
∵四边形OACB为矩形，
∴BC＝OA＝8，BC∥OA，
∴EG∥AC，
∴四边形AEGC为平行四边形，四边形OEGB为平行四边形，
∴CG＝AE＝2，EG＝OB，
∵PE⊥AO，AO∥CB，
∴PG⊥CD，
∴CD＝2CG＝6，
∴DB＝BC﹣CD＝4﹣6＝2，
∵PD＝3，DG＝CG＝3，
∴PG＝4，
∴OB＝EG＝3+4＝9，
∴D（5，2）．
【答案】A．

二十．几何变换的类型（共1小题）
27．（2019•南京）如图，△A'B'C'是由△ABC经过平移得到的，△A'B'C'还可以看作是△ABC经过怎样的图形变化得到？下列结论：①1次旋转；③2次旋转；④2次轴对称．其中所有正确结论的序号是（　　）

A．①④ B．②③ C．②④ D．③④
【详解】解：先将△ABC绕着点A旋转180°得到△AB″C″，再将所得的△AB″C″绕着点B″B'的中点D旋转180°；

先将△ABC沿着B'B的垂直平分线翻折可得△A″B'C″，再将所得的△A″B'C″沿着A'A″的垂直平分线翻折；

【答案】D．
二十一．中心投影（共1小题）
28．（2021•南京）如图，正方形纸板的一条对角线垂直于地面，纸板上方的灯（看作一个点），正方形纸板在地面上形成的影子的形状可以是（　　）

A． B． C． D．
【详解】解：根据正方形纸板的一条对角线垂直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板，
∴在地面上的投影关于对角线对称，
∵灯在纸板上方，
∴上方投影比下方投影要长，
【答案】D．
二十二．条形统计图（共1小题）
29．（2020•南京）党的十八大以来，党中央把脱贫攻坚摆到更加突出的位置．根据国家统计局发布的数据，2012～2019年年末全国农村贫困人口的情况如图所示．

根据图中提供的信息，下列说法错误的是（　　）
A．2019年末，农村贫困人口比上年末减少551万人
B．2012年末至2019年末，农村贫困人口累计减少超过9000万人
C．2012年末至2019年末，连续7年每年农村贫困人口减少1000万人以上
D．为在2020年末农村贫困人口全部脱贫，今年要确保完成减少551万农村贫困人口的任务
【详解】解：A．2019年末，此选项错误；
B．2012年末至2019年末，此选项正确；
C．2012年末至2019年末，此选项正确；
D．为在2020年末农村贫困人口全部脱贫，此选项正确；
【答案】A．
二十三．方差（共1小题）
30．（2018•南京）某排球队6名场上队员的身高（单位：cm）是：180，184，190，192，与换人前相比，场上队员的身高（　　）
A．平均数变小，方差变小 B．平均数变小，方差变大
C．平均数变大，方差变小 D．平均数变大，方差变大
【详解】解：原数据的平均数为＝188，
则原数据的方差为×[（180﹣188）2+（184﹣188）2+（188﹣188）7+（190﹣188）2+（192﹣188）2+（194﹣188）2]＝，
新数据的平均数为＝187，
则新数据的方差为×[（180﹣187）2+（184﹣187）8+（188﹣187）2+（190﹣187）2+（186﹣187）6+（194﹣187）2]＝，
所以平均数变小，方差变小，
【答案】A．