2021中考数学真题知识点分类汇编-图形的对称解答题（含答案）

2021中考数学真题知识点分类汇编-图形的对称解答题（含答案）

一．作图-轴对称变换（共2小题）

1．（2021•宁夏）在平面直角坐标系中，已知线段A1B1与线段AB关于y轴对称，点A1（﹣2，1）是点A的对应点，点B1是点B（4，2）的对应点．

（1）画出线段AB和A1B1；

（2）画出将线段A1B1绕点A1逆时针旋转90°所得的线段A1B2，并求出点B1旋转到点B2所经过的路径长．

2．（2021•深圳）如图所示，在正方形网格中，每个小正方形的边长为1个单位．

（1）过直线m作四边形ABCD的对称图形；

（2）求四边形ABCD的面积．

二．轴对称-最短路线问题（共1小题）

3．（2021•济宁）研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．

（1）阅读材料

立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．

例如，正方体ABCD﹣A′B′C′D′（图1），因为在平面AA′C′C中，AA′与AB相交于点A，所以直线AB与AA′所成的∠BAA′就是既不相交也不平行的两条直线AB与CC′所成的角．

解决问题

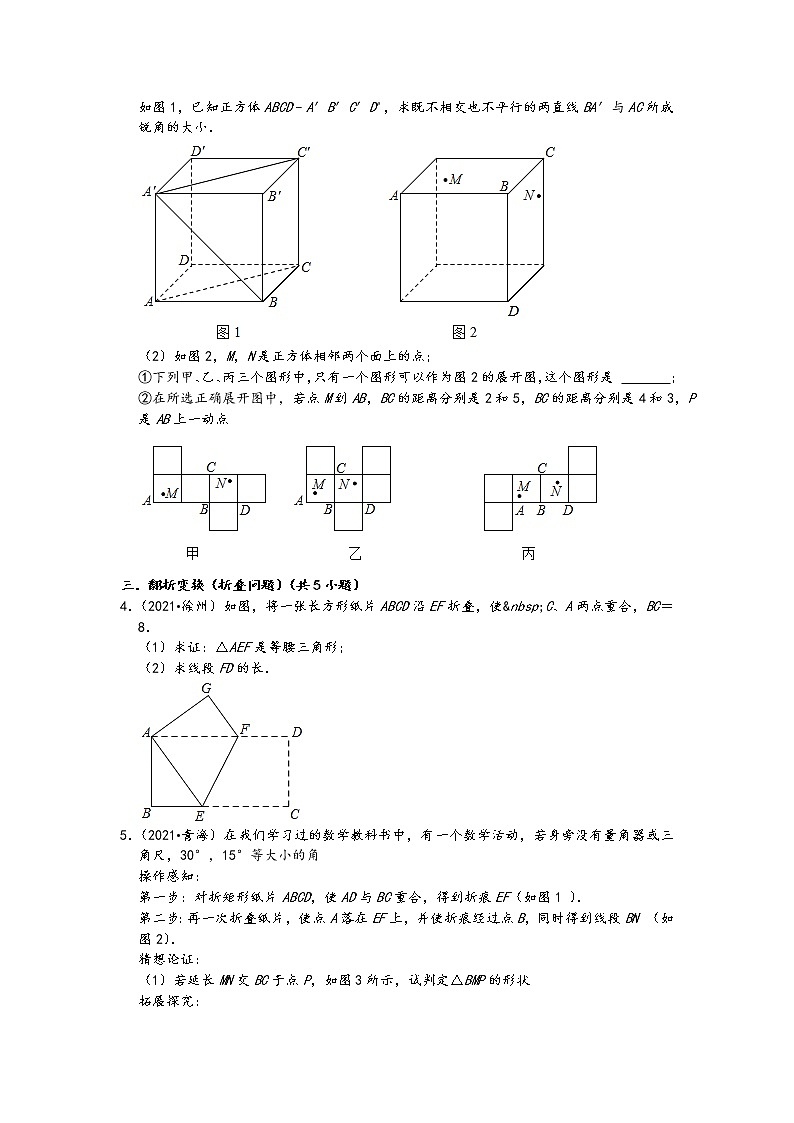
如图1，已知正方体ABCD﹣A′B′C′D'，求既不相交也不平行的两直线BA′与AC所成锐角的大小．

（2）如图2，M，N是正方体相邻两个面上的点；

①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是 　   　；

②在所选正确展开图中，若点M到AB，BC的距离分别是2和5，BC的距离分别是4和3，P是AB上一动点

三．翻折变换（折叠问题）（共5小题）

4．（2021•徐州）如图，将一张长方形纸片ABCD沿EF折叠，使 C、A两点重合，BC＝8．

（1）求证：△AEF是等腰三角形；

（2）求线段FD的长．

5．（2021•青海）在我们学习过的数学教科书中，有一个数学活动，若身旁没有量角器或三角尺，30°，15°等大小的角

操作感知：

第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF（如图1 ）．

第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，同时得到线段BN （如图2）．

猜想论证：

（1）若延长MN交BC于点P，如图3所示，试判定△BMP的形状

拓展探究：

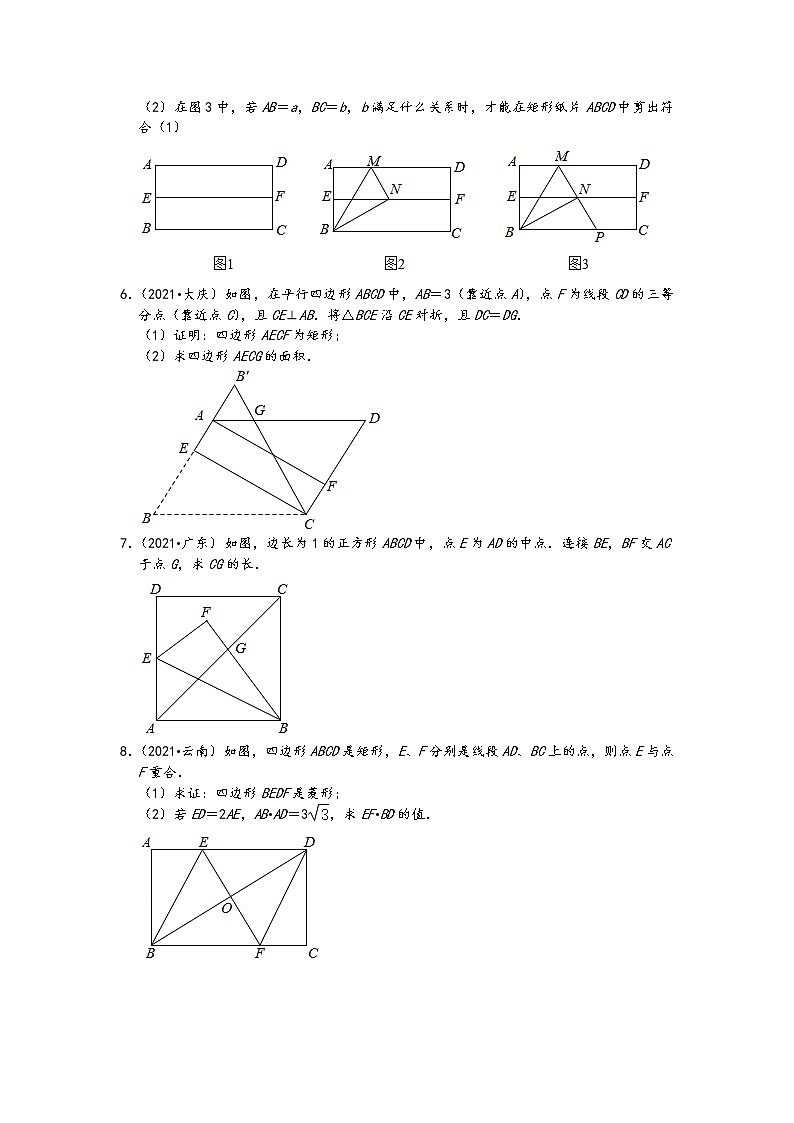
（2）在图3中，若AB＝a，BC＝b，b满足什么关系时，才能在矩形纸片ABCD中剪出符合（1）

6．（2021•大庆）如图，在平行四边形ABCD中，AB＝3（靠近点A），点F为线段CD的三等分点（靠近点C），且CE⊥AB．将△BCE沿CE对折，且DC＝DG．

（1）证明：四边形AECF为矩形；

（2）求四边形AECG的面积．

7．（2021•广东）如图，边长为1的正方形ABCD中，点E为AD的中点．连接BE，BF交AC于点G，求CG的长．

8．（2021•云南）如图，四边形ABCD是矩形，E、F分别是线段AD、BC上的点，则点E与点F重合．

（1）求证：四边形BEDF是菱形；

（2）若ED＝2AE，AB•AD＝3，求EF•BD的值．

参考答案与试题解析

一．作图-轴对称变换（共2小题）

1．（2021•宁夏）在平面直角坐标系中，已知线段A1B1与线段AB关于y轴对称，点A1（﹣2，1）是点A的对应点，点B1是点B（4，2）的对应点．

（1）画出线段AB和A1B1；

（2）画出将线段A1B1绕点A1逆时针旋转90°所得的线段A1B2，并求出点B1旋转到点B2所经过的路径长．

【详解】解：（1）如图，线段AB和A1B1为所作；

（2）如图，线段A4B2为所作，

A1B2＝＝，

所以点B6旋转到点B2所经过的路径长＝＝π．

2．（2021•深圳）如图所示，在正方形网格中，每个小正方形的边长为1个单位．

（1）过直线m作四边形ABCD的对称图形；

（2）求四边形ABCD的面积．

【详解】解：（1）如图所示，四边形A'B'C'D'即为所求；

（2）四边形ABCD的面积＝S△ABD+S△BCD＝×5×1+．

二．轴对称-最短路线问题（共1小题）

3．（2021•济宁）研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．

（1）阅读材料

立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．

例如，正方体ABCD﹣A′B′C′D′（图1），因为在平面AA′C′C中，AA′与AB相交于点A，所以直线AB与AA′所成的∠BAA′就是既不相交也不平行的两条直线AB与CC′所成的角．

解决问题

如图1，已知正方体ABCD﹣A′B′C′D'，求既不相交也不平行的两直线BA′与AC所成锐角的大小．

（2）如图2，M，N是正方体相邻两个面上的点；

①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是 　丙　；

②在所选正确展开图中，若点M到AB，BC的距离分别是2和5，BC的距离分别是4和3，P是AB上一动点

【详解】解：（1）如图1中，连接BC′．

∵A′B＝BC′＝A′C′，

∴△A′BC′是等边三角形，

∴∠BA′C′＝60°，

∵AC∥A′C′，

∴∠C′A′B是两条直线AC与BA′所成的锐角，

∴两直线BA′与AC所成角为60°．

（2）①观察图形可知，图形丙是图2的展开图，

故答案为：丙．

②如图丙中，作点N关于AD的对称点K，连接PN，最小值为线段MK的值．

由题意在Rt△MKJ中，∠MJK＝90°，JK＝2﹣（4﹣2）＝3，

∴MK＝＝＝10，

∴PM+PN的最小值为10．

三．翻折变换（折叠问题）（共5小题）

4．（2021•徐州）如图，将一张长方形纸片ABCD沿EF折叠，使 C、A两点重合，BC＝8．

（1）求证：△AEF是等腰三角形；

（2）求线段FD的长．

【详解】（1）证明：由折叠性质可知，∠AEF＝∠CEF，

由矩形性质可得AD∥BC，

∴∠AFE＝∠CEF，

∴∠AEF＝∠AFE．

∴AE＝AF，

故△AEF为等腰三角形．

（2）解：由折叠可得AE＝CE，设CE＝x＝AE，

则BE＝BC﹣CE＝8﹣x，

∵∠B＝90°，

在Rt△ABE中，有AB2+BE7＝AE2，

即48+（8﹣x）2＝x5，解得：x＝5．

由（1）结论可得AF＝AE＝5，

故FD＝AD﹣AF＝BC﹣AF＝5﹣5＝3．

5．（2021•青海）在我们学习过的数学教科书中，有一个数学活动，若身旁没有量角器或三角尺，30°，15°等大小的角

操作感知：

第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF（如图1 ）．

第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，同时得到线段BN （如图2）．

猜想论证：

（1）若延长MN交BC于点P，如图3所示，试判定△BMP的形状

拓展探究：

（2）在图3中，若AB＝a，BC＝b，b满足什么关系时，才能在矩形纸片ABCD中剪出符合（1）

【详解】解：（1）△BMP是等边三角形，

理由如下：如图3，连接AN，

由折叠的性质可得AE＝BE，EF⊥AB，∠ABM＝∠NBM，

∴AN＝BN，

∴AN＝BN＝AB，

∴△ABN是等边三角形，

∴∠ABN＝60°，

∴∠ABM＝∠NBM＝30°＝∠PBN，

∴∠BMN＝∠BPM＝60°，

∴△BMP是等边三角形；

（2）∵AB＝a，∠ABM＝30°，

∴BM＝＝a，

∵△BMP是等边三角形，

∴BP＝BM＝a，

∵在矩形纸片ABCD中剪出符合（1）中结论的三角形纸片BMP，

∴BC≥BP，

∴b≥a．

6．（2021•大庆）如图，在平行四边形ABCD中，AB＝3（靠近点A），点F为线段CD的三等分点（靠近点C），且CE⊥AB．将△BCE沿CE对折，且DC＝DG．

（1）证明：四边形AECF为矩形；

（2）求四边形AECG的面积．

【详解】（1）证明：∵ABCD是平行四边形，

∴AB∥CD，AB＝CD，

∵点E为线段AB的三等分点（靠近点A），

∴AE＝AB，

∵点F为线段CD的三等分点（靠近点C），

∴CF＝CD，

∴AE＝CF，

又∵AE∥CF，

∴四边形AECF为平行四边形，

∵CE⊥AB，

∴四边形AECF为矩形；

（2）∵AB＝3，

∴AE＝CF＝8，BE＝2，

∵将△BCE沿CE对折得到△ECB'，

∴B'E＝BE＝2，

∴AB'＝8，

∵DC＝DG＝3，

∴∠DGC＝∠DCG，

∵BB'∥CD，

∴∠DCG＝∠B'，

∴∠B'＝∠B'GA，

∴AB'＝AG＝1，

∴DA＝BC＝B'C＝7，

∵AB'∥CD，

∴＝，

∴＝，

∴B'G＝1，

∴△AGB'是等边三角形，

在Rt△BCE中，BC＝4，

∴EC＝2，

∴S四边形AECG＝S△EB'C﹣S△AB'G＝﹣＝．

7．（2021•广东）如图，边长为1的正方形ABCD中，点E为AD的中点．连接BE，BF交AC于点G，求CG的长．

【详解】解：延长BF交CD于H，连接EH．

∵四边形ABCD是正方形，

∴AB∥CD，∠D＝∠DAB＝90°，

∴AC＝＝＝，

由翻折的性质可知，AE＝EF，∠AEB＝∠FEB，

∵点E是AD的中点，

∴AE＝DE＝EF，

∵∠D＝∠EFH＝90°，

在Rt△EHD和Rt△EHF中，

，

∴Rt△EHD≌Rt△EHF（HL），

∴∠DEH＝∠FEH，

∵∠DEF+∠AEF＝180°，

∴2∠DEH+4∠AEB＝180°，

∴∠DEH+∠AEB＝90°，

∵∠AEB+∠ABE＝90°，

∴∠DEH＝∠ABE，

∴△EDH∽△BAE，

∴＝＝，

∴DH＝，CH＝，

∵CH∥AB，

∴＝＝，

∴CG＝AC＝．

8．（2021•云南）如图，四边形ABCD是矩形，E、F分别是线段AD、BC上的点，则点E与点F重合．

（1）求证：四边形BEDF是菱形；

（2）若ED＝2AE，AB•AD＝3，求EF•BD的值．

【详解】解：（1）证明：将△BED沿BD折叠，使E，

∴OE＝OF，EF⊥BD，

∵四边形ABCD是矩形，

∴∠C＝90°，AD∥BC，

∴∠ODE＝∠OBF，

在△OBF和△ODE中，

，

∴△OBF≌△ODE（AAS），

∴OB＝OD，

∵OE＝OF，

∴四边形BFDE是平行四边形，

∵EF⊥BD，

∴四边形BFDE是菱形．

（2）如图，∵AB•AD＝3，

∴S△ABD＝AB•AD＝，

∵ED＝2AE，

∴ED＝AD，

∴S△BDE：S△ABD＝2：2，

∴S△BDE＝，

∴菱形BEDF的面积＝EF•BD＝2S△BDE＝2，

∴EF•BD＝4．