江苏省镇江市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案）

这是一份江苏省镇江市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案），共20页。

江苏省镇江市五年（2017-2021）中考数学真题选择题知识点分类汇编（含答案）

一．有理数的混合运算（共1小题）
1．（2021•镇江）如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算）（　　）

A．1840 B．1921 C．1949 D．2021
二．科学记数法—表示较大的数（共2小题）
2．（2021•镇江）2021年1﹣4月份，全国规模以上工业企业利润总额超25900亿元，其中25900用科学记数法表示为（　　）
A．25.9×103 B．2.59×104 C．0.259×105 D．2.59×105
3．（2017•镇江）我国对“一带一路”沿线国家不断加大投资，目前已为有关国家创造了近1100000000美元税收，其中1100000000用科学记数法表示应为（　　）
A．0.11×108 B．1.1×109 C．1.1×1010 D．11×108
三．科学记数法—表示较小的数（共1小题）
4．（2018•镇江）0.000182用科学记数法表示应为（　　）
A．0182×10﹣3 B．1.82×10﹣4 C．1.82×10﹣5 D．18.2×10﹣4
四．规律型：数字的变化类（共1小题）
5．（2021•镇江）如图，小明在3×3的方格纸上写了九个式子（其中的n是正整数），每行的三个式子的和自上而下分别记为A1，A2，A3，每列的三个式子的和自左至右分别记为B1，B2，B3，其中，值可以等于789的是（　　）

A．A1 B．B1 C．A2 D．B3
五．同底数幂的除法（共2小题）
6．（2020•镇江）下列计算正确的是（　　）
A．a3+a3＝a6 B．（a3）2＝a6 C．a6÷a2＝a3 D．（ab）3＝ab3
7．（2019•镇江）下列计算正确的是（　　）
A．a2•a3＝a6 B．a7÷a3＝a4 C．（a3）5＝a8 D．（ab）2＝ab2
六．解一元一次不等式组（共1小题）
8．（2019•镇江）下列各数轴上表示的x的取值范围可以是不等式组的解集的是（　　）
A．
B．
C．
D．
七．函数的图象（共1小题）
9．（2018•镇江）甲、乙两地相距80km，一辆汽车上午9：00从甲地出发驶往乙地，匀速行驶了一半的路程后将速度提高了20km/h，汽车行驶的路程y（km）与时间x（h），该车到达乙地的时间是当天上午（　　）

A．10：35 B．10：40 C．10：45 D．10：50
八．动点问题的函数图象（共1小题）
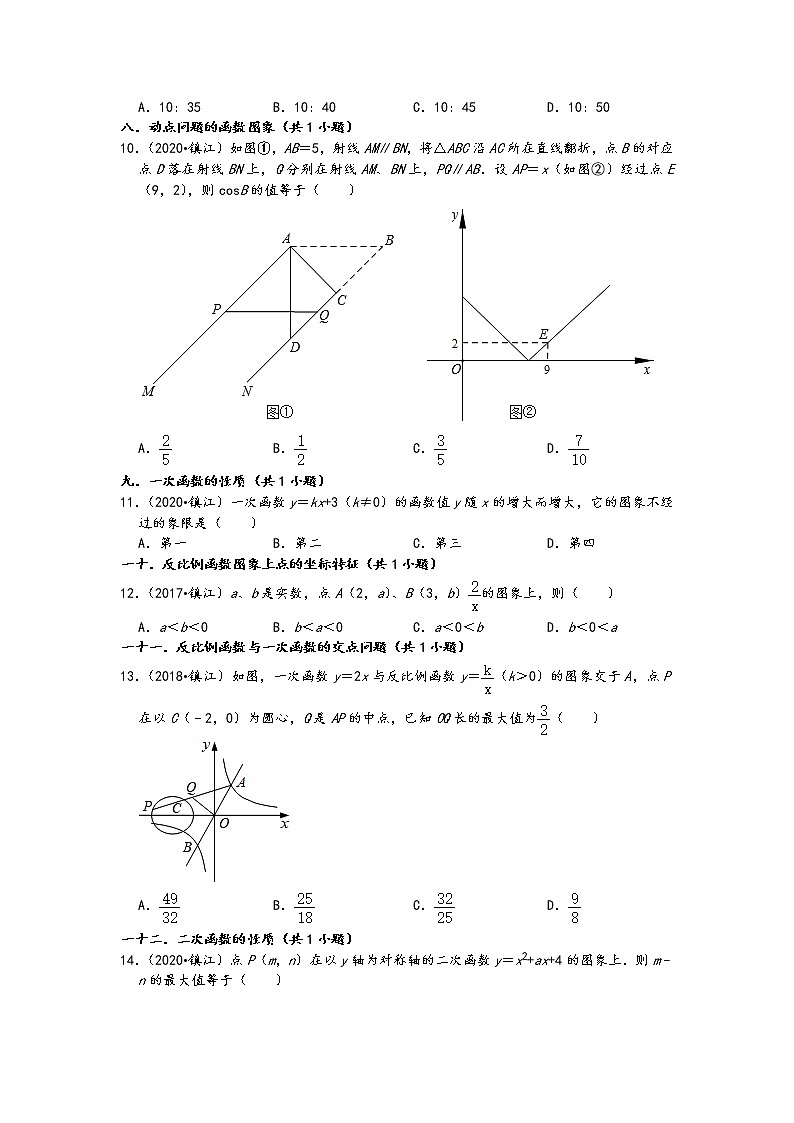
10．（2020•镇江）如图①，AB＝5，射线AM∥BN，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，Q分别在射线AM、BN上，PQ∥AB．设AP＝x（如图②）经过点E（9，2），则cosB的值等于（　　）

A． B． C． D．
九．一次函数的性质（共1小题）
11．（2020•镇江）一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（　　）
A．第一 B．第二 C．第三 D．第四
一十．反比例函数图象上点的坐标特征（共1小题）
12．（2017•镇江）a、b是实数，点A（2，a）、B（3，b）的图象上，则（　　）
A．a＜b＜0 B．b＜a＜0 C．a＜0＜b D．b＜0＜a
一十一．反比例函数与一次函数的交点问题（共1小题）
13．（2018•镇江）如图，一次函数y＝2x与反比例函数y＝（k＞0）的图象交于A，点P在以C（﹣2，0）为圆心，Q是AP的中点，已知OQ长的最大值为（　　）

A． B． C． D．
一十二．二次函数的性质（共1小题）
14．（2020•镇江）点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上．则m﹣n的最大值等于（　　）
A． B．4 C．﹣ D．﹣
一十三．菱形的性质（共1小题）
15．（2019•镇江）如图，菱形ABCD的顶点B、C在x轴上（B在C的左侧），顶点A、D在x轴上方，点E（﹣2，0）为BC的中点（0，6）到EP所在直线的距离取得最大值时，点P恰好落在AB的中点处（　　）

A． B． C． D．3
一十四．圆周角定理（共1小题）
16．（2020•镇江）如图，AB是半圆的直径，C、D是半圆上的两点，则∠CAB等于（　　）

A．10° B．14° C．16° D．26°
一十五．圆内接四边形的性质（共1小题）
17．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝，则∠ABC的度数等于（　　）

A．55° B．60° C．65° D．70°
一十六．切线的性质（共1小题）
18．（2021•镇江）如图，∠BAC＝36°，点O在边AB上，交边AB于点E，F，连接FD（　　）

A．27° B．29° C．35° D．37°
一十七．圆锥的计算（共1小题）
19．（2021•镇江）设圆锥的底面圆半径为r，圆锥的母线长为l，满足2r+l＝6（　　）
A．有最大值π B．有最小值π
C．有最大值π D．有最小值π
一十八．相似三角形的判定与性质（共1小题）
20．（2017•镇江）点E、F分别在平行四边形ABCD的边BC、AD上，BE＝DF，点P在边AB上（n＞1），过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分，将△CDF分成面积为S3、S4的两部分（如图），下列四个等式：
①S1：S3＝1：n
②S1：S4＝1：（2n+1）
③（S1+S4）：（S2+S3）＝1：n
④（S3﹣S1）：（S2﹣S4）＝n：（n+1）
其中成立的有（　　）

A．①②④ B．②③ C．②③④ D．③④
一十九．简单几何体的三视图（共1小题）
21．（2021•镇江）如图所示，该几何体的俯视图是（　　）

A．正方形 B．长方形 C．三角形 D．圆
二十．简单组合体的三视图（共4小题）
22．（2020•镇江）如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体（　　）

A． B． C． D．
23．（2019•镇江）一个物体如图所示，它的俯视图是（　　）

A． B．
C． D．
24．（2018•镇江）如图是由3个大小相同的小正方体组成的几何体，它的左视图是（　　）

A． B． C． D．
25．（2017•镇江）如图是由6个大小相同的小正方体组成的几何体，它的主视图是（　　）

A． B． C． D．
二十一．中位数（共1小题）
26．（2017•镇江）根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（　　）
A．3个 B．4个 C．5个 D．6个
二十二．几何概率（共1小题）
27．（2018•镇江）小明将如图所示的转盘分成n（n是正整数）个扇形，并使得各个扇形的面积都相等，4，6，…，2n（每个区域内标注1个数字，且各区域内标注的数字互不相同），转动转盘1次，若事件“指针所落区域标注的数字大于8”的概率是，则n的取值为（　　）

A．36 B．30 C．24 D．18

参考答案与试题解析
一．有理数的混合运算（共1小题）
1．（2021•镇江）如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算）（　　）

A．1840 B．1921 C．1949 D．2021
【详解】解：把1921代入得：（1921﹣1840+50）×（﹣1）＝﹣131＜1000，
把﹣131代入得：（﹣131﹣1840+50）×（﹣1）＝1921＞1000，
则输出结果为1921+100＝2021．
【答案】D．
二．科学记数法—表示较大的数（共2小题）
2．（2021•镇江）2021年1﹣4月份，全国规模以上工业企业利润总额超25900亿元，其中25900用科学记数法表示为（　　）
A．25.9×103 B．2.59×104 C．0.259×105 D．2.59×105
【详解】解：25900＝2.59×104，
【答案】B．
3．（2017•镇江）我国对“一带一路”沿线国家不断加大投资，目前已为有关国家创造了近1100000000美元税收，其中1100000000用科学记数法表示应为（　　）
A．0.11×108 B．1.1×109 C．1.1×1010 D．11×108
【详解】解：1100000000用科学记数法表示应为1.1×105，
【答案】B．
三．科学记数法—表示较小的数（共1小题）
4．（2018•镇江）0.000182用科学记数法表示应为（　　）
A．0182×10﹣3 B．1.82×10﹣4 C．1.82×10﹣5 D．18.2×10﹣4
【详解】解：0.000182＝2×10﹣7．
【答案】B．
四．规律型：数字的变化类（共1小题）
5．（2021•镇江）如图，小明在3×3的方格纸上写了九个式子（其中的n是正整数），每行的三个式子的和自上而下分别记为A1，A2，A3，每列的三个式子的和自左至右分别记为B1，B2，B3，其中，值可以等于789的是（　　）

A．A1 B．B1 C．A2 D．B3
【详解】解：由题意得：A1＝2n+7+2n+3+6n+5＝789，
整理得：2n＝260，
则n不是整数，故A8的值不可以等于789；
A2＝2n+5+2n+9+3n+11＝789，
整理得：2n＝254，
则n不是整数，故A2的值不可以等于789；
B2＝2n+1+6n+7+2n+13＝789，
整理得：7n＝256＝28，
则n是整数，故B7的值可以等于789；
B3＝2n+2+2n+11+2n+17＝789，
整理得：3n＝252，
则n不是整数，故B3的值不可以等于789；
【答案】B．
五．同底数幂的除法（共2小题）
6．（2020•镇江）下列计算正确的是（　　）
A．a3+a3＝a6 B．（a3）2＝a6 C．a6÷a2＝a3 D．（ab）3＝ab3
【详解】解：a3+a3＝4a3，因此选项A不正确；
（a3）7＝a3×2＝a6，因此选项B正确；
a6÷a2＝a5﹣2＝a4，因此选项C不正确；
（ab）2＝a3b3，因此选项D不正确；
【答案】B．
7．（2019•镇江）下列计算正确的是（　　）
A．a2•a3＝a6 B．a7÷a3＝a4 C．（a3）5＝a8 D．（ab）2＝ab2
【详解】解：A、a2•a3＝a4，故此选项错误；
B、a7÷a3＝a2，正确；
C、（a3）5＝a15，故此选项错误；
D、（ab）7＝a2b2，故此选项错误；
【答案】B．
六．解一元一次不等式组（共1小题）
8．（2019•镇江）下列各数轴上表示的x的取值范围可以是不等式组的解集的是（　　）
A．
B．
C．
D．
【详解】解：由x+2＞a得x＞a﹣2，
A．由数轴知x＞﹣6，∴﹣3x﹣6＜4，与数轴不符；
B．由数轴知x＞0，∴3x﹣5＜0，与数轴相符合；
C．由数轴知x＞2，∴4x﹣6＜0，与数轴不符；
D．由数轴知x＞﹣2，∴﹣x﹣3＜0，与数轴不符；
【答案】B．
七．函数的图象（共1小题）
9．（2018•镇江）甲、乙两地相距80km，一辆汽车上午9：00从甲地出发驶往乙地，匀速行驶了一半的路程后将速度提高了20km/h，汽车行驶的路程y（km）与时间x（h），该车到达乙地的时间是当天上午（　　）

A．10：35 B．10：40 C．10：45 D．10：50
【详解】解：因为匀速行驶了一半的路程后将速度提高了20km/h，
所以1小时后的路程为40km，速度为40km/h，
所以以后的速度为20+40＝60km/h，时间为，
故该车到达乙地的时间是当天上午10：40；
【答案】B．
八．动点问题的函数图象（共1小题）
10．（2020•镇江）如图①，AB＝5，射线AM∥BN，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，Q分别在射线AM、BN上，PQ∥AB．设AP＝x（如图②）经过点E（9，2），则cosB的值等于（　　）

A． B． C． D．
【详解】解：∵AM∥BN，PQ∥AB，
∴四边形ABQP是平行四边形，
∴AP＝BQ＝x，
由图②可得当x＝9时，y＝2，
此时点Q在点D下方Q'处，且BQ'＝x＝3时，如图①所示，

∴BD＝BQ'﹣Q'D＝x﹣y＝7，
∵将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，
∴BC＝CD＝BD＝，
∴cosB＝＝＝，
【答案】D．
九．一次函数的性质（共1小题）
11．（2020•镇江）一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（　　）
A．第一 B．第二 C．第三 D．第四
【详解】解：∵一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，
∴k＞3，该函数过点（0，
∴该函数的图象经过第一、二、三象限，
【答案】D．
一十．反比例函数图象上点的坐标特征（共1小题）
12．（2017•镇江）a、b是实数，点A（2，a）、B（3，b）的图象上，则（　　）
A．a＜b＜0 B．b＜a＜0 C．a＜0＜b D．b＜0＜a
【详解】解：∵y＝﹣，
∴反比例函数y＝﹣的图象位于第二，在每个象限内，
∵点A（5，a），b）在反比例函数y＝﹣，
∴a＜b＜0，
【答案】A．
一十一．反比例函数与一次函数的交点问题（共1小题）
13．（2018•镇江）如图，一次函数y＝2x与反比例函数y＝（k＞0）的图象交于A，点P在以C（﹣2，0）为圆心，Q是AP的中点，已知OQ长的最大值为（　　）

A． B． C． D．
【详解】解：连接BP，
由对称性得：OA＝OB，
∵Q是AP的中点，
∴OQ＝BP，
∵OQ长的最大值为，
∴BP长的最大值为×2＝3，
如图，当BP过圆心C时，过B作BD⊥x轴于D，
∵CP＝7，
∴BC＝2，
∵B在直线y＝2x上，
设B（t，7t），BD＝﹣2t，
在Rt△BCD中，由勾股定理得：BC2＝CD8+BD2，
∴23＝（t+2）2+（﹣6t）2，
t＝0（舍）或﹣，
∴B（﹣，﹣），
∵点B在反比例函数y＝（k＞8）的图象上，
∴k＝﹣＝；
【答案】C．

一十二．二次函数的性质（共1小题）
14．（2020•镇江）点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上．则m﹣n的最大值等于（　　）
A． B．4 C．﹣ D．﹣
【详解】解：∵点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上，
∴a＝4，
∴n＝m2+4，
∴m﹣n＝m﹣（m6+4）＝﹣m2+m﹣6＝﹣（m﹣）5﹣，
∴当m＝时，m﹣n取得最大值，
【答案】C．
一十三．菱形的性质（共1小题）
15．（2019•镇江）如图，菱形ABCD的顶点B、C在x轴上（B在C的左侧），顶点A、D在x轴上方，点E（﹣2，0）为BC的中点（0，6）到EP所在直线的距离取得最大值时，点P恰好落在AB的中点处（　　）

A． B． C． D．3
【详解】解：如图1中，当点P是AB的中点时，连接EF．
∵E（﹣2，8），6），
∴OE＝2，OF＝5，
∴EF＝＝2，
∵∠FGE＝90°，
∴FG≤EF，
∴当点G与E重合时，FG的值最大．
如图3中，当点G与点E重合时，PE交BD于J．

∵PA＝PB，BE＝EC＝a，
∴PE∥AC，BJ＝JH，
∵四边形ABCD是菱形，
∴AC⊥BD，BH＝DH＝，
∴PE⊥BD，
∵∠BJE＝∠EOF＝∠PEF＝90°，
∴∠EBJ＝∠FEO，
∴△BJE∽△EOF，
∴＝，
∴＝，
∴a＝，
∴BC＝2a＝，
【答案】A．
一十四．圆周角定理（共1小题）
16．（2020•镇江）如图，AB是半圆的直径，C、D是半圆上的两点，则∠CAB等于（　　）

A．10° B．14° C．16° D．26°
【详解】解：连接BD，如图，
∵AB是半圆的直径，
∴∠ADB＝90°，
∴∠BDC＝∠ADC﹣∠ADB＝106°﹣90°＝16°，
∴∠CAB＝∠BDC＝16°．
【答案】C．

一十五．圆内接四边形的性质（共1小题）
17．（2019•镇江）如图，四边形ABCD是半圆的内接四边形，AB是直径，＝，则∠ABC的度数等于（　　）

A．55° B．60° C．65° D．70°
【详解】解：连接AC，
∵四边形ABCD是半圆的内接四边形，
∴∠DAB＝180°﹣∠C＝70°，
∵＝，
∴∠CAB＝∠DAB＝35°，
∵AB是直径，
∴∠ACB＝90°，
∴∠ABC＝90°﹣∠CAB＝55°，
【答案】A．

一十六．切线的性质（共1小题）
18．（2021•镇江）如图，∠BAC＝36°，点O在边AB上，交边AB于点E，F，连接FD（　　）

A．27° B．29° C．35° D．37°
【详解】解：连接OD，
∵⊙O与边AC相切于点D，
∴∠ADO＝90°，
∵∠BAC＝36°，
∴∠AOD＝90°﹣36°＝54°，
∴∠AFD＝AOD＝，
【答案】A．

一十七．圆锥的计算（共1小题）
19．（2021•镇江）设圆锥的底面圆半径为r，圆锥的母线长为l，满足2r+l＝6（　　）
A．有最大值π B．有最小值π
C．有最大值π D．有最小值π
【详解】解：∵2r+l＝6，
∴l＝3﹣2r，
∴圆锥的侧面积S侧＝πrl＝πr（6﹣8r）＝﹣2π（r2﹣6r）＝﹣2π[（r﹣）2﹣]＝﹣2π（r﹣）2+π，
∴当r＝时，S侧有最大值π．
【答案】C．
一十八．相似三角形的判定与性质（共1小题）
20．（2017•镇江）点E、F分别在平行四边形ABCD的边BC、AD上，BE＝DF，点P在边AB上（n＞1），过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分，将△CDF分成面积为S3、S4的两部分（如图），下列四个等式：
①S1：S3＝1：n
②S1：S4＝1：（2n+1）
③（S1+S4）：（S2+S3）＝1：n
④（S3﹣S1）：（S2﹣S4）＝n：（n+1）
其中成立的有（　　）

A．①②④ B．②③ C．②③④ D．③④
【详解】解：由题意∵AP：PB＝1：n（n＞1），AD∥l∥BC，
∴＝（）2，S4＝n2S1，＝（）2，
整理得：S2＝n（n+8）S1，S4＝（4n+1）S1，
∴S6：S4＝1：（8n+1），故①错误，
∴（S1+S8）：（S2+S3）＝[S5+（2n+1）S4]：[n（n+2）S1+n5S1]＝1：n，故③正确，
∴（S4﹣S1）：（S2﹣S7）＝[n2S1﹣S8]：[n（n+2）S1﹣（5n+1）S1]＝4：1，故④错误，
【答案】B．
一十九．简单几何体的三视图（共1小题）
21．（2021•镇江）如图所示，该几何体的俯视图是（　　）

A．正方形 B．长方形 C．三角形 D．圆
【详解】解：从上面看该几何体，所看到的图形是三角形．
【答案】C．
二十．简单组合体的三视图（共4小题）
22．（2020•镇江）如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体（　　）

A． B． C． D．
【详解】解：从正面看是一个正方形，正方形的右上角是一个小正方形，
【答案】A．
23．（2019•镇江）一个物体如图所示，它的俯视图是（　　）

A． B．
C． D．
【详解】解：俯视图从图形上方观察即可得到，
【答案】D．
24．（2018•镇江）如图是由3个大小相同的小正方体组成的几何体，它的左视图是（　　）

A． B． C． D．
【详解】解：如图所示：它的左视图是：
．
【答案】D．
25．（2017•镇江）如图是由6个大小相同的小正方体组成的几何体，它的主视图是（　　）

A． B． C． D．
【详解】解：该主视图是：底层是3个正方形横放，右上角有一个正方形，
【答案】C．
二十一．中位数（共1小题）
26．（2017•镇江）根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（　　）
A．3个 B．4个 C．5个 D．6个
【详解】解：当a＝1时，有19个数据，则中位数是38；
当a＝2时，有20个数据，则中位数是38；
当a＝8时，有21个数据，则中位数是38；
当a＝4时，有22个数据，则中位数是38；
当a＝5时，有23个数据，则中位数是38；
当a＝2时，有24个数据，则中位数是38.5；
故该组数据的中位数不大于38，则符合条件的正整数a的取值共有：5个．
【答案】C．
二十二．几何概率（共1小题）
27．（2018•镇江）小明将如图所示的转盘分成n（n是正整数）个扇形，并使得各个扇形的面积都相等，4，6，…，2n（每个区域内标注1个数字，且各区域内标注的数字互不相同），转动转盘1次，若事件“指针所落区域标注的数字大于8”的概率是，则n的取值为（　　）

A．36 B．30 C．24 D．18
【详解】解：∵“指针所落区域标注的数字大于8”的概率是，
∴＝，
解得：n＝24，
【答案】C．