
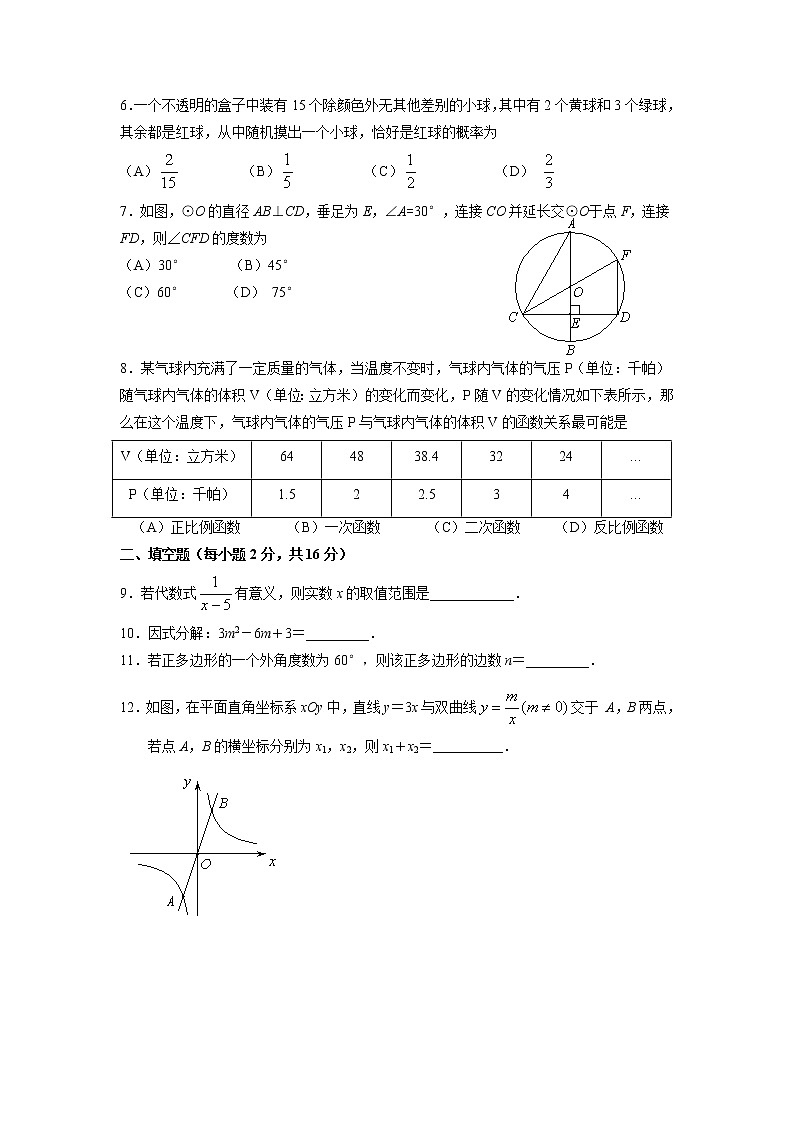
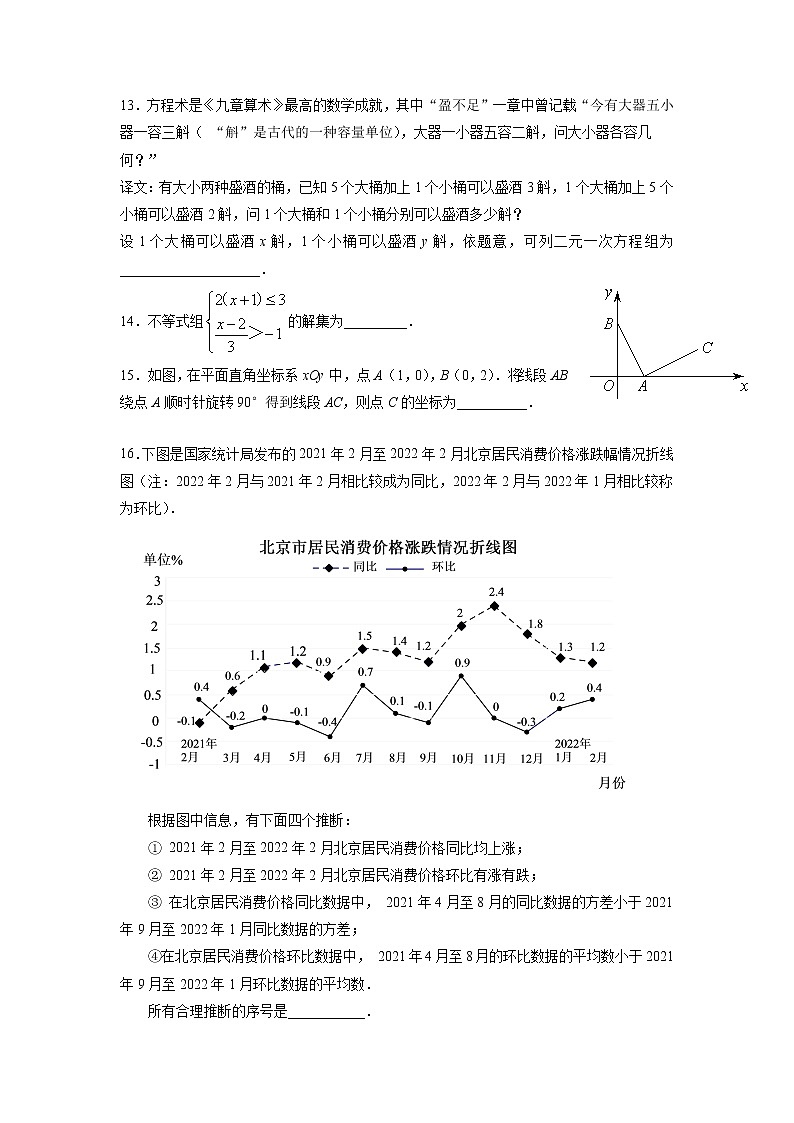
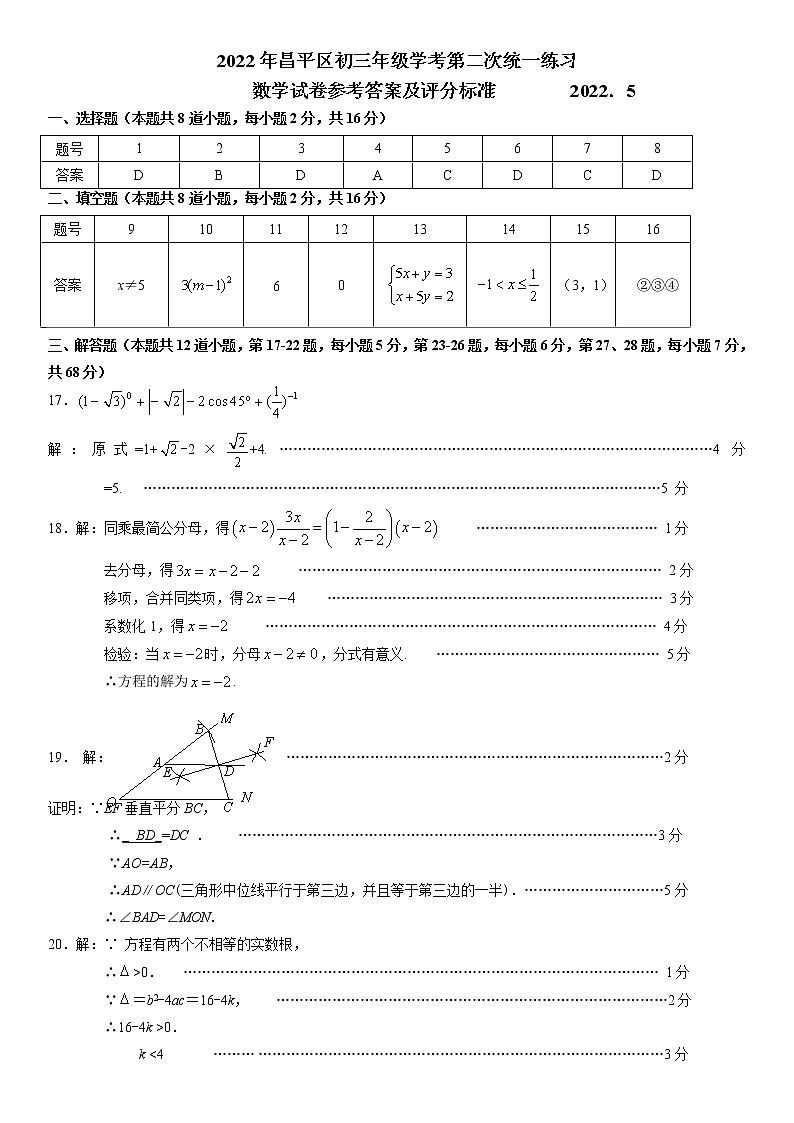
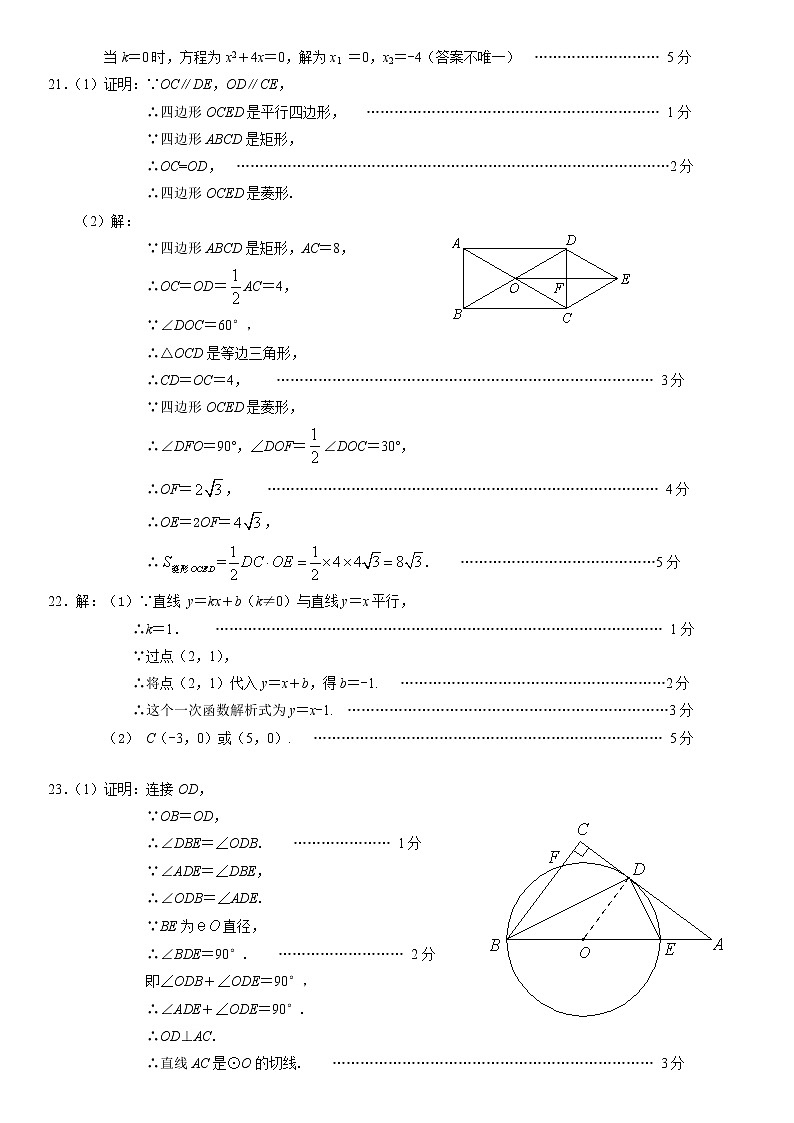
2022年北京市昌平区中考数学二模试题(含答案)
展开2022年昌平区初三年级学考第二次统一练习
数学试卷参考答案及评分标准 2022.5
一、选择题(本题共8道小题,每小题2分,共16分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | B | D | A | C | D | C | D |
二、填空题(本题共8道小题,每小题2分,共16分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 | x≠5 | 6 | 0 | (3,1) | ②③④ |
三、解答题(本题共12道小题,第17-22题,每小题5分,第23-26题,每小题6分,第27、28题,每小题7分,共68分)
17.
解:原式=1+-2×+4. …………………………………………………………………………………4分 =5. …………………………………………………………………………………………………5 分
18.解:同乘最简公分母,得 ………………………………… 1分
去分母,得 …………………………………………………………………… 2分
移项,合并同类项,得 ……………………………………………………………… 3分
系数化1,得 ………………………………………………………………………… 4分
检验:当时,分母,分式有意义. ………………………………………… 5分
∴方程的解为.
19. 解: ………………………………………………………………………2分
证明:∵EF垂直平分BC,
∴_ BD_=DC . ………………………………………………………………………………3分
∵AO=AB,
∴AD∥OC(三角形中位线平行于第三边,并且等于第三边的一半).…………………………5分
∴∠BAD=∠MON.
20.解:∵ 方程有两个不相等的实数根,
∴>0. ………………………………………………………………………………………… 1分
∵=b2-4ac=16-4k, …………………………………………………………………………2分
∴16-4k >0.
k <4 ……… ……………………………………………………………………………3分
当k=0时,方程为x2+4x=0,解为x1 =0,x2=-4(答案不唯一) ……………………… 5分
21.(1)证明:∵OC∥DE,OD∥CE,
∴四边形OCED是平行四边形, ……………………………………………………… 1分
∵四边形ABCD是矩形,
∴OC=OD, …………………………………………………………………………………2分
∴四边形OCED是菱形.
(2)解:
∵四边形ABCD是矩形,AC=8,
∴OC=OD=AC=4,
∵∠DOC=60°,
∴△OCD是等边三角形,
∴CD=OC=4, ……………………………………………………………………… 3分
∵四边形OCED是菱形,
∴∠DFO=90°,∠DOF=∠DOC=30°,
∴OF=, ………………………………………………………………………… 4分
∴OE=2OF=,
∴. ……………………………………5分
22.解:(1)∵直线 y=kx+b(k≠0)与直线y=x平行,
∴k=1. …………………………………………………………………………………… 1分
∵过点(2,1),
∴将点(2,1)代入y=x+b,得b=-1. …………………………………………………2分
∴这个一次函数解析式为y=x-1. ……………………………………………………………3分
(2) C(-3,0)或(5,0). ………………………………………………………………… 5分
23.(1)证明:连接OD,
∵OB=OD,
∴∠DBE=∠ODB. ………………… 1分
∵∠ADE=∠DBE,
∴∠ODB=∠ADE.
∵BE为直径,
∴∠BDE=90°. ……………………… 2分
即∠ODB+∠ODE=90°,
∴∠ADE+∠ODE=90°.
∴OD⊥AC.
∴直线AC是⊙O的切线. …………………………………………………………… 3分
(2)解:∵⊙O的半径为3,
∴OB=OD=3. ………………………………………………………………………… 4分
∵,∠ODA=90°,
∴.
∴OA=5. ………………………………………………………………………………… 5分
∴AB=8.
∵∠C=90°,
∴.
∴BC=. ……………………………………………………………………………… 6分
24.解:(1)1 ; ………………………………………………………………………………………… 2分
(2)
………………… 4分
(3)3;18. ……………………………………………………………………………………… 6分
25. 解:(1)16. ……………………………………………………………………………………… 2分
(2)p1<p2
甲小区,p1=6+6+2=14(户);乙小区中位数高于平均数,则p2至少为15户,
∴p1<p2 . ……………………………………………………………………………………… 4分
(3)由题意得:300×=180(户).…………………………………………………………… 6分
答:甲小区中用气量超过15立方米约180户.
26. 解:(1)若抛物线过点(4,-1).
①由题可知,抛物线过点(0,-1).
∵点(4,-1)与(0,-1)关于对称轴对称,
∴对称轴为直线x=2. ……………………………………………………………………2分
②∵当时,图象在x轴的下方,当时,图象在x轴的上方,
抛物线的对称轴为直线x=2,
∴抛物线必过点(-1,0)和(5,0).
∴把(4,-1),(-1,0)代入
得,抛物线的表达式为. ………………………………… 4分
(2). ……………………………………………………………… 6分
27.(1)①
…………………………… 2分
解:② ∵点A关于OP的对称点为点B,
∴OA=OB.
∵∠MON=α,
∴∠OBA=OAB=90°-. ………………………………………………………………… 3分
∵AE⊥OB于点E,
∴∠BAE=90°-(90°-)=. …………………………………………………… 4分
(2)α=45°. …………………………………………………………………………………………… 5分
证明如下:
∵∠MON=45°,∠AEO=90°,
∴∠AOE=∠OAE=45°.
∴AE=OE,
∵OP平分∠MON,
∴∠DOE=∠MON=22.5°.
∵∠BAE=α=22.5°
∴∠DOE=∠BAE,
∵∠OED=∠AEB=90°,
∴△ODE≌△ABE. ………………………………………………………………………… 6分
∴OD=AB.
∵AQ平分∠OAE,
∴∠EAQ=∠OAE=22.5°.
∴∠BAF=45°.
∵点A的对称点为点B,
∴AF=FB.
∴△AFB是等腰直角三角形,
∴AB=AF.
∴OD =AF. ……………………………………………………………………………… 7分
28.(1)画图正确. …………………………………………………………………………………………2分
(2)由题意可知点C横坐标x的取值范围是. ………………………………………… 4分
(3)OC的最小值为,OC的最大值为 ……………………………………………… 6分
最大时AC的长为. …………………………………………………………… 7分
2023北京市昌平区中考二模数学(pdf版 含答案): 这是一份2023北京市昌平区中考二模数学(pdf版 含答案),共9页。
2023年北京市昌平区中考数学二模试卷(含解析): 这是一份2023年北京市昌平区中考数学二模试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北京市昌平区新道临川校2021-2022学年中考数学最后一模试卷含解析: 这是一份北京市昌平区新道临川校2021-2022学年中考数学最后一模试卷含解析,共24页。试卷主要包含了考生要认真填写考场号和座位序号,解分式方程﹣3=时,去分母可得,下列运算结果正确的是等内容,欢迎下载使用。












