湖南省张家界市2022年初中毕业学业考试模拟数学试题（二）(word版含答案)

张家界市2022年初中毕业学业考试模拟检测试卷(2)

数 学

注意事项:

    1．本卷为试题卷，考生应在答题卡上作答，在试题卷、草稿纸上答题无效。

2．本试卷共三道大题，满分100分，时量120分钟。

一、选择题（本大题共8小题，共24分）

1．2022的相反数是（   ）

 A．2022   B．   C．   D．

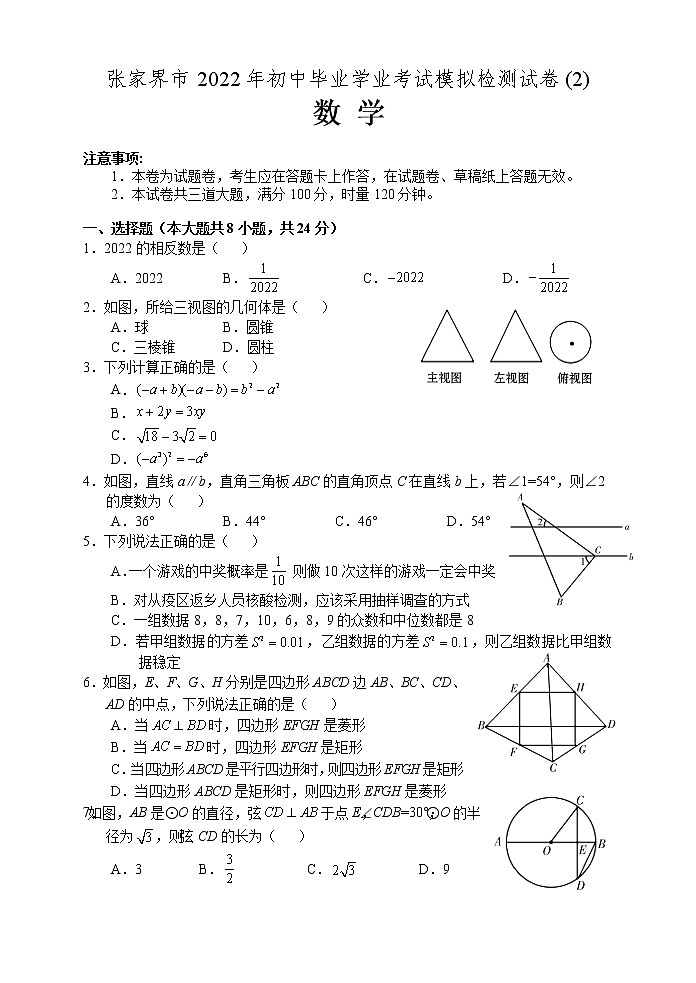
2．如图，所给三视图的几何体是（   ）

 A．球       B．圆锥  

 C．三棱锥    D．圆柱

3．下列计算正确的是（   ）

 A． 

 B．
 C． 

 D．

4．如图，直线a∥b，直角三角板ABC的直角顶点C在直线b上，若∠1=54°，则∠2的度数为（   ）

 A．36°   B．44°   C．46°   D．54°

5．下列说法正确的是（   ）

 A．一个游戏的中奖概率是 则做10次这样的游戏一定会中奖
 B．对从疫区返乡人员核酸检测，应该采用抽样调查的方式

 C．一组数据8，8，7，10，6，8，9 的众数和中位数都是8

D．若甲组数据的方差，乙组数据的方差，则乙组数据比甲组数据稳定

6．如图，E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点，下列说法正确的是（   ）

 A．当时，四边形EFGH是菱形
 B．当时，四边形EFGH是矩形
 C．当四边形ABCD是平行四边形时，则四边形EFGH是矩形
 D．当四边形ABCD是矩形时，则四边形EFGH是菱形

7．如图，AB是⊙O的直径，弦于点E，∠CDB=30°，⊙O的半径为，则弦CD的长为（   ）

 A．3        B．        C．      D．9

8．如图，抛物线与x轴交于点(4，0)，其对称轴为直线，结合图象给出下列结论：①；
②；
③当时，y随x的增大而增大；
④关于x的一元二次方程有两个不相等的实数根．
其中正确的结论有（   ）

 A．1个     B．2个    C．3个      D．4个 

二、填空题（本大题共6小题，共18分）

9．因式分解：______．

10．华为Mate20系列搭载了麒麟980芯片，这个被华为称之为全球首个7纳米工艺的AI芯片，拥有8个全球第一，7纳米就是0.000000007米．数据0.000000007用科学记数法表示为______．

11．一个正多边形的一个外角等于45°，则这个正多边形的边数是______．

12．不等式的最大整数解是______．

13．如图，在△ABC中，，∠ACB=90°，以AB中点D为圆心，作圆心角为90°的扇形DEF，点C恰好在弧EF上，则图中阴影部分面积为______．
                    

           第13题图                                第14题图

14．如图，在平面直角坐标系中，直线与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，顶点D恰好落在双曲线，若将正方形沿x轴向左平移b个单位长度后，点C恰好落在该双曲线上，则b的值为___________．

三、解答题（本大题共9小题，共58分）

15．(5分)计算：．




 

16．(5分)先化简再求值：，其中．


 

17．(6分)如图，在△ABC中，∠BAC=90°，点D是BC中点，AE∥BC，CE∥AD．                                            

（1）求证：四边形ADCE是菱形;

（2）过点D作DF⊥CE于点F，∠B=60°，AB=6，求EF的长．

 

18．(5分)第5代移动通信技术简称5G，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，小明和小强分别用5G与4G下载一部600兆的公益片，小明比小强所用的时间快140秒，求该地4G与5G的下载速度分别是每秒多少兆？



 

19．(6分)阅读材料：我们知道，两数之积大于0，那么这两数同号，即，则或；两数之积小于0，那么这两数异号，即，则或．
解决问题：

（1）分解因式：__________________；

（2）解不等式：．






 

20．(6分)我国航天事业捷报频传，天舟二号于2021年5月29日成功发射，震撼人心当天舟二号从地面到达点A处时，在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米，它沿铅垂线上升7.5秒后到达B处，此时在P处测得B点的仰角∠DPB为45°，求天舟二号从A处到B处的平均速度.(结果精确到，取，)

21．(6分)“双减”背景下，某市中小学全面开展了“周六托管”服务为了让周六托管课程能更好促进学生全面发展，某校开设了A(篮球)、B(足球)、C(古筝)、D(创意写生)四门拓展性托管课程．该校为了解学生对四门拓展性托管课程的喜爱情况，从全校学生中随机抽取部分学生进行调查问卷，通过分析整理绘制了如下两幅统计图．请根据两幅统计图中的信息回答下列问题：

（1）求参与调查的学生中，喜爱足球课程的学生人数，并补全条形图；

（2）若从参与调查的2名男生和2名女生中随机抽取2名学生，进行四门课程的学习体验，请用列表法或画树状图的方法求抽取到的两名学生为一名男生和一名女生的概率．

22．(9分)如图，在△ABC中，点O是BC中点，以O为圆心，BC为直径作圆刚好经过A点，延长BC于点D，连接AD已知．

（1）求证：①AD是⊙O的切线；
②△ACD∽△BAD ；

（2）若BD=8，，求⊙O的半径．

23．(10分)如图，已知点，，在抛物线上．
（1）求抛物线解析式；(4分)

（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；(3分)

（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使？若存在，求出Q点坐标；若不存在，说明理由．(3分)
 

张家界市2022年初中毕业学业考试模拟检测试卷(2)

数学参考答案

9．         10．            11．8  

12．2                       13．             14．2
 

15．解：原式
           

16．解：
       当时，原式．
 

17．（1）证明：∵AE∥DC，EC∥AD，
  ∴四边形ADCE是平行四边形，
  ∵∠BAC=90°，点D是BC的中点，
  ∴AD=BD=CD，
  ∴平行四边形ADCE是菱形；
  （2）解：∵∠B =60°，AD=BD，
  ∴△ABD是等边三角形，
  ∴∠ADB=60°，AD=AB=6，
  ∵AD∥CE，
  ∴∠DCE=60°，
  ∵CD=AD=6，
  ∴，
  ∵四边形ADCE是菱形，
  ∴CE=CD=6，
  ∴EF=3．
 

18．解：设该地4G的下载速度是每秒x兆，则该地5G的下载速度是每秒15x兆，
   由题意得：，
   解得：，
   经检验：是原分式方程的解，且符合题意，
   ，
 答：该地4G的下载速度是每秒4兆，则该地5G的下载速度是每秒60兆．
 

19．（1）  
    （2），
        

  则有，解得：，则不等式组无解；
  ，解得：，则不等式组的解集是：，
  故不等式组的解集为：．
 

20．解：由题意可得：∠APD=30°，∠BPD=45°，AP=6km，∠BDP=90°，
  在Rt△BPD中，∵∠APD=30°，AP=6km，∠ADP=90°，cos∠APD=cos30°=，
  ∴，，
  在Rt△APD中，
  ∵∠BPD=45°，，，∠BDP=90°，，
  ∴，
  故，
  则天舟二号从A处到B处的平均速度约为：，
 答：天舟二号从A处到B处的平均速度约为293m/s．
 

21．解：（1）∵被调查的总人数为（人），
   ∴喜爱B课程人数为(人)，
   补全条形图如下：
                     
 

（2）画树状图为：
       
 共有12种等可能的结果，其中抽取的两人恰好是一名男生和一名女生结果数为8，
所以抽取的两人恰好是一名男生和一名女生概率为．
22．（1）①证明：连接AO，
  ∵BC是直径，
  ∴∠BAC=90°，
  ∴∠B+∠ACO=90°，
  ∵OA=OC，
  ∴∠ACO=∠OAC，
  ∵∠CAD=∠B．
  ∴∠DAO=∠CAD+∠CAO=90°，
  ∴OA⊥AD，
  ∴AD是⊙O的切线；
  ②证明：∵∠CAD=∠B，∠ADC=∠BDA，
  ∴△ACD∽△BAD；
  （2）解：∵∠BAC=90°，
  ∴，
  ∵△ACD∽△BAD，
  ∴，
  ∴，
  ∴，
  ∴半径．
 

23．解：（1）设抛物线的解析式为，
  将代入得，
  解得：，
  抛物线的解析式为．

   （2）过点P作，交BC于点D，连接PC，BP，
  设直线BC的解析式为，则
  
  解得：
  直线BC的解析式为．
  设点，则，
  ，
  ，
  又，
  ，
 整理得：
  ，
  解得：， ，
  点P的坐标为或(2,1)．
 （3）存在．
  ，，
  ，
  ，
  ，
  点Q为△ABC外接圆与拋物线对称轴在x轴下方的交点．
  设△ABC 外接圆圆心为M，
  则．
  设圆M的半径为x，则Rt△CMB 中，由勾股定理可知
  ，
  即，解得：(负值舍去)，
  ，
  的垂直平分线为直线，AB的垂直平分线为直线．
  点M为直线与的交点，
  即，
  点Q的坐标为