沪科版九年级上册21.3 二次函数与一元二次方程课文内容ppt课件

这是一份沪科版九年级上册21.3 二次函数与一元二次方程课文内容ppt课件，共21页。PPT课件主要包含了学习目标及重难点，课程导入，x-1或x3，-1x3，课程讲授，新课推进，拓广探索，x-2或x4，-2x4，-1＜x＜3等内容，欢迎下载使用。
1. 理解二次函数y=ax2+bx+c与一元二次不等式之间的关系；(重点)2. 会用二次函数图象求一元二次不等式的解集.(难点)
问题1：上节课学到的一元二次方程ax2+bx+c=0(a≠0)的根和二次函数y=ax2+bx+c(a≠0)的图象,它们存在着怎样的联系?
问题2：一次函数与一元一次不等式有怎样的联系？那你可以猜测到二次函数与一元二次不等式的联系吗？
通过一次函数与一元一次方程的关系，探究到二次函数与一元二次方程的关系，那么不等式呢
我们观察一次函数的图象，一次函数与一次不等式之间有什么关系呢
例1 函数y=ax2+bx+c的图象如图，那么方程ax2+bx+c=0的根是 _____ _____;不等式ax2+bx+c>0的解集 是___________;不等式ax2+bx+c2的解集是___________;不等式ax2+bx+c0（a≠0）的解集是x≠2 的一切实数，那么函数y=ax2+bx+c的图象与 x轴有____ 个交点，坐标是______.方程ax2+bx+c=0的根是______.
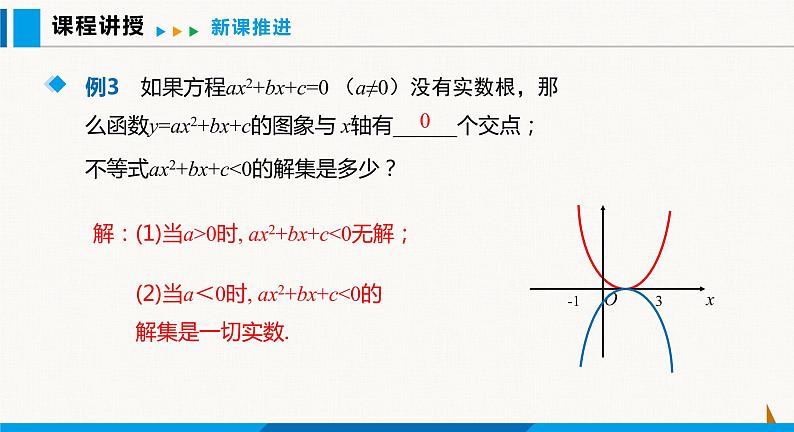
例3 如果方程ax2+bx+c=0 （a≠0）没有实数根，那么函数y=ax2+bx+c的图象与 x轴有______个交点；不等式ax2+bx+c0时, ax2+bx+c