
高中数学北师大版 (2019)必修 第一册第四章 对数运算和对数函数3 对数函数3.2 对数函数y=log2 x的图像和性质课时训练
展开对数函数的图象和性质
[A级 基础巩固]
1.函数y=与y=logbx互为反函数,则a与b的关系是( )
A.ab=1 B.a+b=1
C.a=b D.a-b=1
解析:选A 由函数y=与y=logbx互为反函数得=b,化简得ab=1,故选A.
2.(多选)函数f(x)=loga(x+2)(0<a<1)的图象过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:选BCD 因为0<a<1,所以函数y=logax的图象单调递减,在y轴右侧,过定点(1,0).函数f(x)=loga(x+2)的图象是把y=logax的图象向左平移2个单位,所以图象过第二、三、四象限.
3.设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为,则a=( )
A. B.2
C.2 D.4
解析:选D 因为a>1,所以y=logax在[a,2a]上是增函数.所以loga(2a)-logaa=,
即loga2=,所以a=2,解得a=4.
4.设a,b,c均为正数,且ea=-ln a,e-b=-ln b,e-c=ln c,则( )
A.a<b<c B.c<b<a
C.c<a<b D.b<a<c
解析:选A 如图是函数y=ex,y=e-x,y=ln x,y=-ln x的图象,a是y=ex与y=-ln x的图象交点的横坐标,b是y=e-x与y=-ln x的图象交点的横坐标,c是y=e-x与y=ln x的图象交点的横坐标,由图可得a<b<c.故选A.
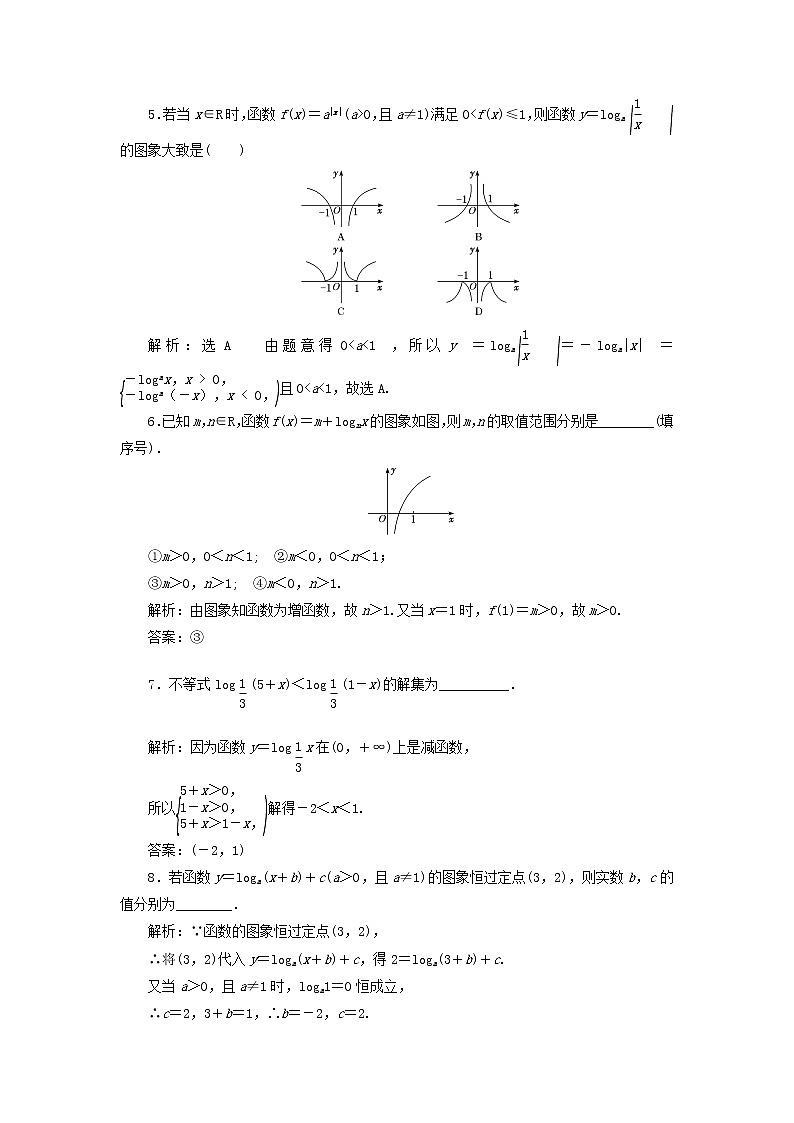
5.若当x∈R时,函数f(x)=a|x|(a>0,且a≠1)满足0<f(x)≤1,则函数y=loga的图象大致是( )
解析:选A 由题意得0<a<1,所以y=loga=-loga|x|=且0<a<1,故选A.
6.已知m,n∈R,函数f(x)=m+lognx的图象如图,则m,n的取值范围分别是________(填序号).
①m>0,0<n<1; ②m<0,0<n<1;
③m>0,n>1; ④m<0,n>1.
解析:由图象知函数为增函数,故n>1.又当x=1时,f(1)=m>0,故m>0.
答案:③
7.不等式log(5+x)<log(1-x)的解集为__________.
解析:因为函数y=logx在(0,+∞)上是减函数,
所以解得-2<x<1.
答案:(-2,1)
8.若函数y=loga(x+b)+c(a>0,且a≠1)的图象恒过定点(3,2),则实数b,c的值分别为________.
解析:∵函数的图象恒过定点(3,2),
∴将(3,2)代入y=loga(x+b)+c,得2=loga(3+b)+c.
又当a>0,且a≠1时,loga1=0恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
答案:-2,2
9.若-1<loga <1(a>0,且a≠1),求实数a的取值范围.
解:∵-1<loga <1,
∴loga <loga <logaa.
当a>1时,0<<<a,则a>;
当0<a<1时,>>a>0,则0<a<.
故实数a的取值范围是∪.
10.已知f(x)=|log3x|.
(1)画出这个函数的图象;
(2)当0<a<2时f(a)>f(2),利用函数图象求出a的取值范围.
解:(1)图象如图所示:
(2)令f(a)=f(2),即|log3a|=|log32|,
解得a=或a=2.
从图象可知,当0<a<时,满足f(a)>f(2),
所以a的取值范围是.
[B级 综合运用]
11.设函数f(x)=loga(x+b)(a>0,且a≠1)的图象过点(2,1),其反函数的图象过点(2,8),则a+b等于( )
A.3 B.4
C.5 D.6
解析:选B f(x)=loga(x+b)的反函数的图象过点(2,8),因此函数f(x)的图象过点(8,2).
又f(x)的图象过点(2,1),则
所以解得或
又a>0,所以
所以a+b=4.
12.设x1,x2,x3均为实数,x1K=log2(x1+1),x2K=log3x2,x3K=log2x3,则( )
A.x1<x3<x2 B.x3<x2<x1
C.x3<x1<x2 D.x2<x1<x3
解析:选A 作出函数y=,y=log2(x+1),y=log3x,y=log2x的大致图象,如图所示,由三个等式可知,三个交点A、B、C的横坐标从左向右依次为x1,x3,x2,所以x1<x3<x2.故选A.
13.已知实数a,b满足等式log2a=log3b,给出下列五个关系式:①a>b>1;②b>a>1;③a<b<1;④b<a<1;⑤a=b.其中可能成立的关系式是________.(填序号)
解析:实数a,b满足等式log2a=log3b,即y=log2x在x=a处的函数值和y=log3x在x=b处的函数值相等,当a=b=1时,log2a=log3b=0,此时⑤成立;令log2a=log3b=1,可得a=2,b=3,由此知②成立,①不成立;令log2a=log3b=-1,可得a=,b=,由此知④成立,③不成立.综上可知,可能成立的关系式为②④⑤.
答案:②④⑤
14.设函数f(x)=ln(ax2+2x+a)的定义域为M.
(1)若1∉M,2∈M,求实数a的取值范围;
(2)若M=R,求实数a的取值范围.
解:(1)由题意M={x|ax2+2x+a>0}.
由1∉M,2∈M可得
化简得解得
所以a的取值范围为∅.
(2)由M=R可得ax2+2x+a>0恒成立.
当a=0时,不等式可化为2x>0,解得x>0,显然不合题意;
当a≠0时,由二次函数的图象可知Δ=22-4×a×a<0,且a>0,即化简得解得a>1.
所以a的取值范围为(1,+∞).
[C级 拓展探究]
15.(1)函数y=log2(x-1)的图象是由y=log2x的图象如何变化得到的?
(2)如图,在直角坐标系中作出y=|log2(x-1)|的图象(不要求写作法);
(3)设函数y=与函数y=|log2(x-1)|的图象的两个交点的横坐标分别为x1,x2,设M=(x1-2)(x2-2),请判断M的符号.
解:(1)函数y=log2(x-1)的图象是由y=log2x的图象向右平移1个单位长度得到的.
(2)在直角坐标系中作出y=|log2(x-1)|的图象,如图所示.
(3)不妨设x1<x2,作出y=的图象,如图,由图知1<x1<2,2<x2<3.∴M=(x1-2)(x2-2)<0,故M的符号为负.
数学必修 第一册第四章 指数函数与对数函数4.4 对数函数习题: 这是一份数学必修 第一册第四章 指数函数与对数函数4.4 对数函数习题,共6页。
高中数学北师大版 (2019)必修 第一册3.1 对数函数的概念精练: 这是一份高中数学北师大版 (2019)必修 第一册3.1 对数函数的概念精练,共3页。
高中数学北师大版 (2019)必修 第一册2 指数幂的运算性质课后复习题: 这是一份高中数学北师大版 (2019)必修 第一册2 指数幂的运算性质课后复习题,共4页。













