四川省南充市2022届高三上学期10月高考适应性考试（零诊） 数学（理）练习题

南充市高2022届高考适应性考试(零诊)

理科数学

本试卷23小题，满分150分。考试用时120分钟。

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.己知z(1－i)2＝3＋4i，其中i为虚数单位，则复数z在复平面内对应的点在第(     )象限。

A.一       B.二      C.三     D.四

2.已知集合U＝{x|－1<x≤2}，B＝{y|y＝}，则∁UB＝

A.(－1，0)     B.[－1，0)     C.(－1，0]     D.[－1，0]

3.2021年是中国共产党成立100周年，某学校团委在7月1日前，开展了“奋斗百年路，启航新征程”党史知识竞赛。团委工作人员将进入决赛的100名学生的分数(满分100分且每人的分值为整数)分成6组：[70，75)，[75，80)，[80，85)，[85，90)，[90，95)，[95，100]得到如图所示的频率分布直方图，则下列关于这100名学生的分数说法错误的是

A.分数的中位数一定落在区间[85，90)       B.分数的众数可能为96

C.分数落在区间[80，85)内的人数为25       D.分数的平均数约为85

4.已知实数x，y满足，则z＝x＋3y的最小值为

A.     B.     C.4     D.6

5.一个袋中共有8个除了颜色外完全相同的球，其中白球5个，黑球3个，从袋中任取3个球，所取得3个球中恰有2个白球，1个黑球的概率为

A.     B.     C.     D.

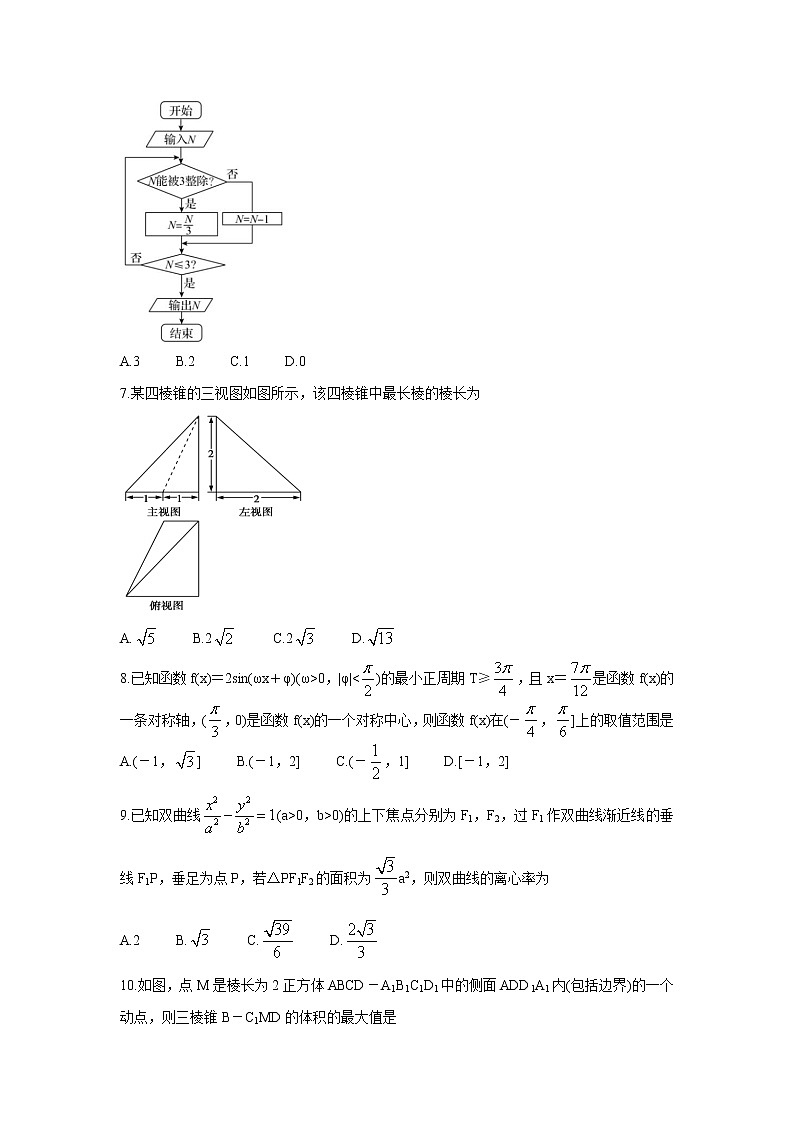
6.执行如图所示的程序框图，若输入N的值为28，则输出N的值为

A.3     B.2     C.1     D.0

7.某四棱锥的三视图如图所示，该四棱锥中最长棱的棱长为

A.     B.2     C.2     D.

8.已知函数f(x)＝2sin(ωx＋φ)(ω>0，|φ|<)的最小正周期T≥，且x＝是函数f(x)的一条对称轴，(，0)是函数f(x)的一个对称中心，则函数f(x)在(－，]上的取值范围是

A.(－1，]     B.(－1，2]     C.(－，1]     D.[－1，2]

9.已知双曲线(a>0，b>0)的上下焦点分别为F1，F2，过F1作双曲线渐近线的垂线F1P，垂足为点P，若△PF1F2的面积为a2，则双曲线的离心率为

A.2     B.     C.     D.

10.如图，点M是棱长为2正方体ABCD－A1B1C1D1中的侧面ADD1A1内(包括边界)的一个动点，则三棱锥B－C1MD的体积的最大值是

A.     B.     C.     D.

11.已知函数f(x)＝x5－3x3＋ln－2sinx，且a＝－f(－θ)，b＝f(sinθ)，c＝f(tanθ)，(0<θ<)，则

A.a>b>c     B.a>c>b     C.b>c>a     D.b>a>c

12.在△ABC中，设a，b，c分别为角A，B，C对应的边，记△ABC的面积为S，且bsinB＋2csinC＝4asinA，则的最大值为

A.     B.     C.     D.

二、填空题：本题共4小题，每小题5分，共20分。

13.在二项式(－x)6的展开式中，常数项是          。

14.已知向量＝(1，－2)，＝(－2，1)，＝(3，λ)。若//(3＋)，则λ＝          。

15.若f(x)是定义在R上函数，且y＝f(x－2)的图形关于直线x＝2对称，当x<0时，f(x)＋xf'(x)<0，且f(－3)＝0，则不等式f(x)>0的解集为          。

16.已知过点T(－1，1)作抛物线C：y2＝2px的两条切线，切点为A，B，直线AB经过抛物线C的焦点F，则|TA|2＋|TB|2＝          。

三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17－21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

(一)必考题：共60分。

17.(本小题满分12分)某校近期将举行秋季田径运动会，运动会设田赛和径赛两类比赛，该校对高一年级1200名学生的参与意向进行了调查(每位同学的参与意向只能选择田赛和径赛中的一个，不能都选，也不能都不选)，其中男生650人，女生550人，所得统计数据如下表所示：(单位：人)

(I)请将题中表格补充完整，并判断能否有99%把握认为“是否选择田赛与性别有关”？

(II)某位同学打算参加径赛中的三个比赛项目：短跑，长跑，跨栏跑。若该同学参加短跑获奖的概率是，参加长跑和跨栏跑获奖的概率都是，且参加各个比赛项目是否获奖相互独立。用ζ表示该同学在这次运动会中获奖的项目个数，求随机变量ζ的分布列和数学期望。

(参考数据：12302＝1512900，65×55×9＝32175，1512900÷32175≈47)

附：；

18.(本小题满分12分)数列{an}的前n项之和为Sn，a1＝1，an＋1＝pan＋q(p，q为常数)。

(I)当p＝1，q＝2时，求数列{}的前n项之和Tn；

(II)当p＝2，q＝1时，求Sn。

19.(本小题满分12分)已知四棱锥P－ABCD的底面为直角梯形，AB//DC，∠DAB＝90°，PA⊥AD，且PA＝AB＝2AD＝2DC，PB＝AB，点M在线段PB上，。

(I)证明：平面PAC⊥平面PBC；

(II)求直线CM与平面PCD所成角的正弦值。

20.(本小题满分12分)椭圆E：的离心率e＝，A，B分别为椭圆E的左、右顶点，P为椭圆E上任意一点，△PAB面积的最大值为2。

(I)求椭圆E的方程；

(II)过点F(1，0)且斜率不为零的直线交椭圆E于M，N两点，过点M作直线x＝4的垂线，垂足为H，证明：直线HN与x轴的交点为定点。

21.(本小题满分12分)已知函数f(x)＝lnx－，(a∈R)。

(I)试讨论f(x)的单调性；

(II)求证：。

(二)选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。

22.[选修4－4：坐标系与参数方程](10分)

在平面直角坐标系xOy中，曲线C的参数方程为(θ∈[0，2π))，在以坐标原点为极点，x轴的正半轴为极轴的极坐标系中，直线l的方程为ρcos(θ＋)＝。

(I)求曲线C的普通方程和直线l的直角坐标方程；

(II)已知点P(0，－2)，直线l与曲线C相交A，B两点，点M是弦AB的中点，求三角形OPM的面积。

23.[选修4－5：不等式选讲](10分)

己知函数f(x)＝|2x＋1|－|x－a|(a∈R)。

(I)若a＝1，解不等式f(x)<1；

(II)若f(x)>－2恒成立，求a的取值范围。