人教版八年级下册18.2.1 矩形表格教案设计

教师姓名

单位名称

填写时间

学科

数学

年级/册

八年级

教材版本

人教版

课题名称

第18章 直角三角形斜边上的中线等于斜边的一半（矩形的性质）

难点名称

直角三角形斜边上的中线性质定理的证明与应用。

难点分析

从知识角度分析为什么难

因为利用对称的性质构造全等三角形，以及构造平行四边形证明直角三角形斜边上的中线等于斜边的一半，总结中点辅助线模型，思维过程交为复杂，学生容易出错。

从学生角度分析为什么难

因为学生能以“直角三角形斜边上的中线等于斜边的一半”思想为指导，通过折纸、测量、猜想、验证等活动，经历一个完整的数学探索过程．这种在合情推理的基础上，经过严格证明，难免让学生觉得繁琐。

难点教学方法

通过教师的启发引导，充分运用多媒体教学手段，开展小组讨论、探讨交流、归纳总结来突出主线，层层深入，逐一突破难点。

教学环节

教学过程

导入

复习引入：

矩形的定义？

定义：有一个角是直角的平行四边形叫做矩形。

矩形的性质？

性质1  矩形的四个角都是直角。

性质2  矩形的对角线相等且平分

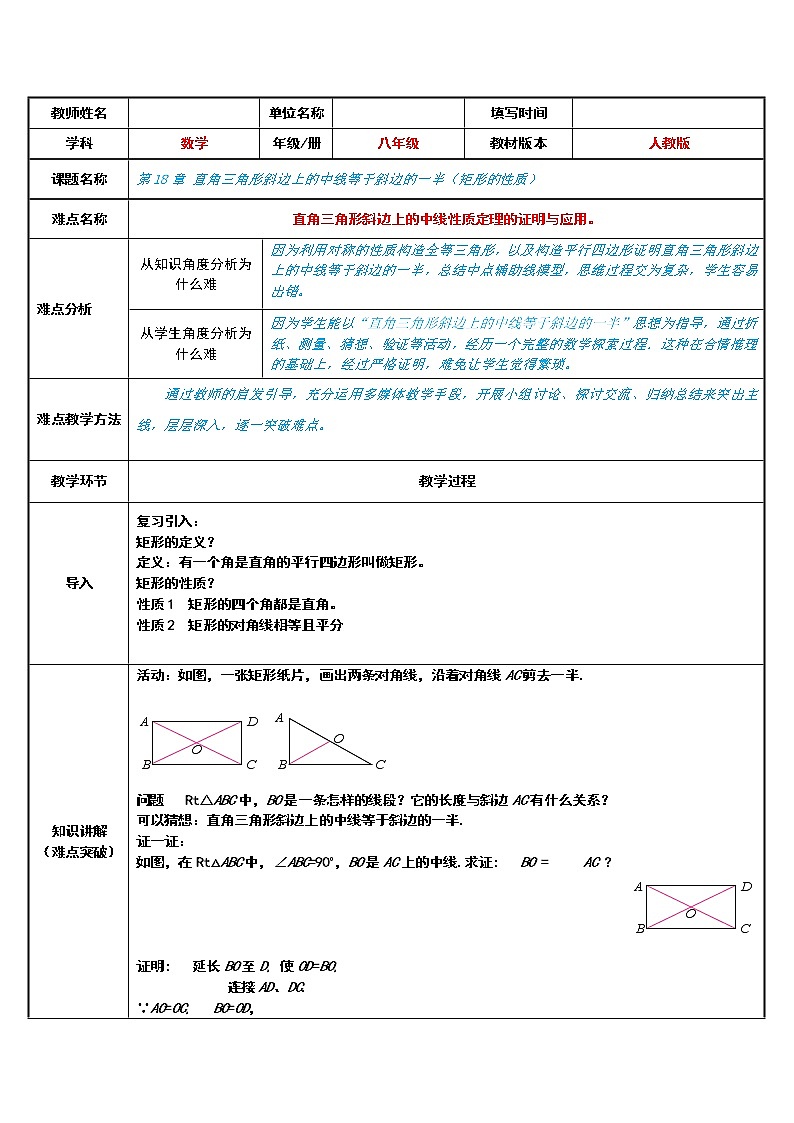
知识讲解

（难点突破）

活动：如图，一张矩形纸片，画出两条对角线，沿着对角线AC剪去一半.

问题   Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么关系？

可以猜想：直角三角形斜边上的中线等于斜边的一半.

证一证：

如图，在Rt△ABC中，∠ABC=90°，BO是AC上的中线.求证:   BO =     AC ?

证明:   延长BO至D, 使OD=BO,

             连接AD、DC.

∵AO=OC,   BO=OD，

∴四边形ABCD是平行四边形.

∵∠ABC=90°,

∴平行四边形ABCD是矩形，

∴AC=BD   ∴BO=    BD=    AC.

性质：直角三角形斜边上的中线等于斜边的一半.

课堂练习

（难点巩固）

如图，在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.

(1)若BD=3cm,则AC =_____cm;

(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD =        

     _____cm.

例4  如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．

(1)若AB＝10，AC＝8，

求四边形AEDF的周长；

(2)求证：EF垂直平分AD.

小结

1、解决上述问题运用了什么知识？

全等三角形, 矩形的判定和性质，中位线，轴对称

2、解决上述问题体现了什么数学思想方法？

数学思想：转化（化归）

利用已知(求证)作出恰当的辅助线，构造全等三角形 。

3、中点辅助线模型

最终总结了：直角三角形斜边上的中线等于斜边的一半.