2021学年19.2.2 一次函数教案设计

教师姓名

单位名称

填写时间

学科

数学

年级/册

八年级（下）

教材版本

人教版

课题名称

第十九章19.2.2一次函数的图象和性质

难点名称

能根据一次函数的图象理解一次函数的性质；灵活运用一次函数的图象与性质解答有关问题

难点分析

从知识角度分析为什么难

知识点本身内容抽象：函数的表示法之一是图象法，即通过坐标系中的直线上的点的坐标反映变量之间的对应关系。这种表示方法将数量关系直观化、形象化，从而可以数形结合的研究问题。学生容易理解。为今后进一步学习数学打下牢固基础.。

从学生角度分析为什么难

学生抽象逻辑思维仍然需要加强，学生不仅应着眼于具体的数学知识，更要认识相关的数学思想方法，不断加深对它们的领会，从更高的角度认识问题的本质。

难点教学方法

1.通过数形结合的思想方法探究一次函数的图象，

2.类比正比例函数的性质，结合一次函数图象归纳一次函数性质。

教学环节

教学过程

导入

回顾正比例函数、一次函数定义，正比例函数图象和性质，提问如何研究一次函数的图象和性质

知识讲解

（难点突破）

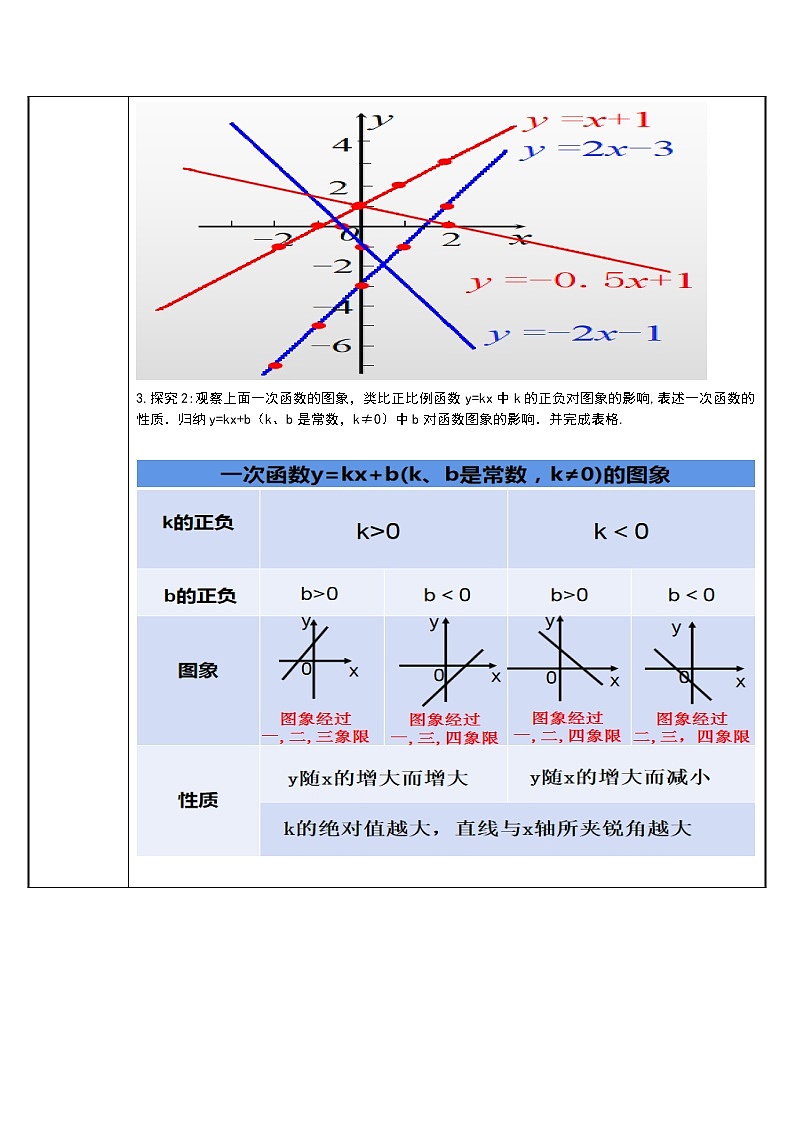
1.画一次函数 y =2x-3 和 y =x+1的图象．

2.探究1:观察上面一次函数的图象，它与正比例函数图象有什么异同点？

相同点：一次函数图象也是一条直线。不同点：一次函数图象不经过原点。

总结：

画一次函数的图像时，只要描出合适关系式的两点，再连接两点即可。我们通常选取图像与y轴和x轴的交点坐标，即：（0，b）和（-b/k，0 ）这两个点。

用两点法在同一坐标系中画出函数y=-2x-1与y=-0.5x+1的图象．

3.探究2:观察上面一次函数的图象，类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质．归纳y=kx+b（k、b是常数，k≠0）中b对函数图象的影响．并完成表格.

课堂练习

（难点巩固）

1.点已知M(-3,  4)在一次函数y=ax+1的图象上,则a的值是  -1     .

2．直线y=2x-3与x轴交点坐标为  （3/2,0）  ，与y轴交点坐标为  （0，-3） ，图象经过第 一、三、四   象限，y随x增大而___增大__．

3.一次函数y=-x-5的图象不经过    第一    象限.

4.已知函数y=(m-2)x+n的图象经过一、二、三象限，则m、n的取值范围为  m＞2，n＞0 .

5.一次函数y=x-2的大致图象为  （ C  ）

6.已知函数 y = kx的图象在二、四象限，那么函数y = kx-k的图象可能是（ A  ）

7. P1(x1，y1)，P2(x2，y2)是一次函数y=-0.5x+3图象上的两点，下列判断中，正确的是( D   )

A.y1＞y2       B.当x1＜x2时，y1＜y2        C.y1＜y2        D.当x1＜x2时，y1＞y2

小结