2022年河北省邯郸市邯山区中考数学质检试卷（一）（含解析）

这是一份2022年河北省邯郸市邯山区中考数学质检试卷（一）（含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年河北省邯郸市邯山区中考数学质检试卷（一）副标题题号一二三总分得分      一、选择题（本大题共16小题，共42.0分）如图，已知三条直线相交于点，则的对顶角是A.
B.
C.
D. 将用科学记数法表示为A.  B.  C.  D. 下列直线不是等边三角形的对称轴的是A. 三条中位线所在的直线 B. 三条高所在的直线
C. 三条中线所在的直线 D. 三条角平分线所在的直线下列运算正确的是A.  B.
C.  D. 如图，要得到从点观测点的俯角，可以测量
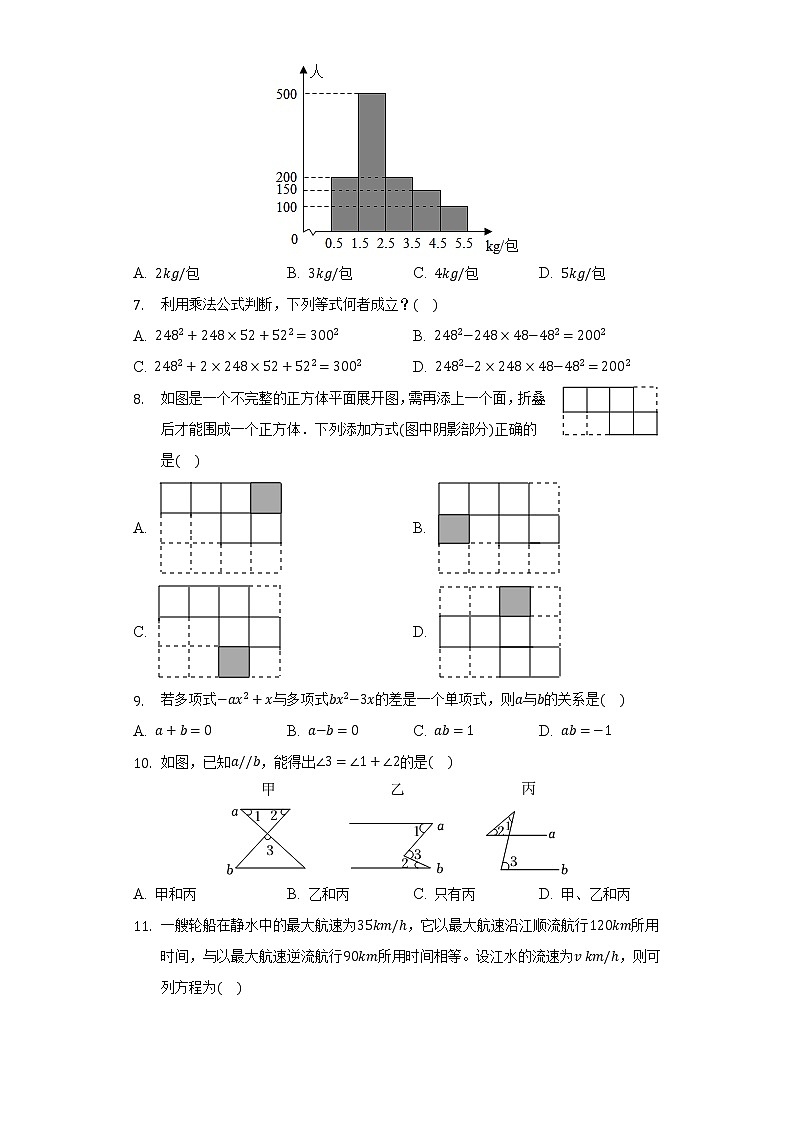
A.  B.  C.  D. 商店准备确定一种包装袋来包装大米，经市场调查后，做出如下统计图，请问选择什么样的包装最合适
A. 包 B. 包 C. 包 D. 包利用乘法公式判断，下列等式何者成立？A.  B.
C.  D. 如图是一个不完整的正方体平面展开图，需再添上一个面，折叠后才能围成一个正方体．下列添加方式图中阴影部分正确的是A.  B.
C.  D. 若多项式与多项式的差是一个单项式，则与的关系是A.  B.  C.  D. 如图，已知，能得出的是
A. 甲和丙 B. 乙和丙 C. 只有丙 D. 甲、乙和丙一艘轮船在静水中的最大航速为，它以最大航速沿江顺流航行所用时间，与以最大航速逆流航行所用时间相等。设江水的流速为，则可列方程为A.  B.
C.  D. 已知，线段，如图是用直尺，三角板和圆规作菱形边长为的步骤，它的依据是
A. 四条边都相等的四边形是菱形
B. 两组对边分别相等的四边形是平行四边形，有一组邻边相等的平行四边形是菱形
C. 两组对边分别平行的四边形是平行四边形，有一组邻边相等的平行四边形是菱形
D. 两组对边分别平行的四边形是平行四边形，两条对角线互相垂直的平行四边形是菱形如图，数轴上的，，三点所表示的数分别为，，，且原点为，根据图中各点位置，判断下列选项不正确的是
A.  B.
C.  D. 已知，，，若为整数且，则的值为A.  B.  C.  D. 如图，在平面直角坐标系中，为直角三角形，，轴，为的外心．若点的坐标为，点的坐标为，则点的坐标为A.
B.
C.
D. 如图，已知是半圆的直径，点，将分成相等的三段弧，点在上．若点在上，，对于下列三个结论判断正确的是
结论Ⅰ：若点在的中点处，则；
结论Ⅱ：当点在上时，的最小值为；
结论Ⅲ：若，则点在上．A. Ⅰ和Ⅲ都对 B. Ⅰ和Ⅱ都不对 C. Ⅱ对Ⅲ不对 D. Ⅰ不对Ⅲ对 二、填空题（本大题共3小题，共12.0分）计算下列各小题．
的立方根是______；
______．求下列多边形的边数．
若一个边形的每一个外角都等于，则______；
若一个边形的内角和是外角和的倍，则______．如图，已知平面直角坐标系中的四个点：，，．
若点和点在双曲线的两侧，则的整数值为______；
在经过这四个点中的三个点的二次函数的图象中，的最大值是______． 三、解答题（本大题共7小题，共66.0分）已知一列数，，，．
求最大的数和最小的数的差；
若再添上一个有理数，使得五个有理数的和为，求的值．






 如图为朵朵披萨屋的公告，设一个夏威夷披萨调涨前的售价为元．
会员购买一个夏威夷披萨，涨价前的花费为______元；涨价后的花费为______元；
若公告前后会员实际购买一个夏威夷披萨的费用相差最多为元，试通过列不等式的方法确定一个夏威夷披萨调涨前的售价最高为多少元．







 一个不透明的口袋中已有三张卡片，卡片上分别标有数字，，小明向口袋中再放入一张标有数字的卡片，发现此时四张卡片上数字的中位数和众数相同．
数字是多少；
已知摸到每张卡片的可能性相同．小颖先从装有四张卡片的袋子中拿出一张卡片，记下数字后放回并搅匀；再从袋子中随机拿出一张卡片记下数字，用列表法如图求小颖同学两次拿到卡片上的数字都是的概率．又拿
先拿______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______ ______






 如图，在一平面内，从左到右，点，，，，均在同一直线上．线段，线段，是，的中点．固定点以及线段，让线段绕点顺时针旋转．
连接，，，．
求证：四边形为平行四边形；
当时，求四边形的周长；
连接某个时刻，直线与线段旋转形成的扇形相切于点，如图所示，求此时线段扫过的扇形面积．







 如图，将南北向的中山路与东西向的和平路看成两条直线，十字路口记作点甲从中山路上的点处出发，骑车向北匀速直行；与此同时，乙从点出发，沿和平路步行向东匀速直行，设出发时，甲、乙两人与点的距离分别为，已知，与之间的函数关系如图所示．
在甲到达点之前，分别求，关于的函数解析式；
当甲、乙出发时，求他们之间的直线距离；
直接写出两人与点的距离相等时，甲、乙两人出发的时间．







 如图，已知抛物线：与直线：相交于点和点．
求和的值；
若直线与线段交于点，与抛物线交于点，求，两点间距离的最大值；
是直线上的一个动点，将点向左平移个单位长度得到点，若线段与抛物线只有一个公共点，直接写出点的横坐标的取值范围．







 已知在矩形中，，是边，上的点，过点作的垂线交边于点．
【发现】如图，以为直径作，点 ______填“在”或“不在”上；当时，的值是______；
【论证】如图，当时，求证：；
【探究】如图当，是边，的中点时，若，，求的长；
【拓展】如图将矩形换为平行四边形，在平行四边形中，，，，是上的动点，过点在的右侧作的垂线，且有，当点落在平行四边形的边所在的直线上时，直接写出的长．








答案和解析 1.【答案】
 【解析】解：由对顶角的定义可知，与是对顶角，
故选：．
根据“一个角的两边分别是另一个角两边的反向延长线，这两个角是对顶角”进行判断即可．
本题考查对顶角，掌握“一个角的两边分别是另一个角两边的反向延长线，这两个角是对顶角”是正确判断的前提．
 2.【答案】
 【解析】解：．
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．
此题考查科学记数法的表示方法，科学记数法的表示形式为的形式，表示时关键要确定的值以及的值．
 3.【答案】
 【解析】解：等边三角形的同边上的中线、高、角平分线重合，故三条高所在的直线、三条中线所在的直线、三条角平分线所在的直线都是对称轴，而三条中位线所在的直线不是对称轴．
故选：．
根据等腰三角形的“三线合一”的性质作答．
本题主要考查了三角形中位线定理，等边三角形的判定与性质以及轴对称的性质．如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
 4.【答案】
 【解析】解：、，故A不符合题意；
B、，故B不符合题意；
C、与不属于同类项，不能合并，故C不符合题意；
D、，故D符合题意；
故选：．
利用同底数幂的除法的法则，合并同类项的法则，同底数幂的乘法的法则，幂的乘方的法则对各项进行运算即可．
本题主要考查同底数幂的除法，合并同类项，幂的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握．
 5.【答案】
 【解析】解：从点观测点的俯角，也就是从点观测点的仰角，
即要得到从点观测点的俯角，可以测量．
故选：．
根据俯角的定义和俯角的定义直接求解即可．
本题考查解直角三角形的应用仰角俯角问题．熟练掌握俯角和仰角的定义是解题关键．
 6.【答案】
 【解析】解：由图知这组数据的众数为，取其组中值，
故选：．
最合适的包装即顾客购买最多的包装，而顾客购买最多的包装质量即这组数据的众数，取所得范围的组中值即可．
本题主要考查频数率分布直方图，解题的关键是根据最合适的包装即顾客购买最多的包装，并根据频数分布直方图得出具体的数据．
 7.【答案】
 【解析】解：选项A：不符合完全平方公式的特征且计算错误，完全平方公式的中间一项为，所以不符合题意；
选项B：不符合完全平方公式特征且计算错误，最后一项应为，所以不符合题意；
选项C：，所以符合题意；
选项D：不符合完全平方公式特征且计算错误，最后一项应为，所以不符合题意．
故选：．
根据完全平方公式的特征进行判断，然后根据公式特点进行计算．
本题主要考查了完全平方公式的特征，识记且熟练运用完全平方公式：是解答问题的关键．
 8.【答案】
 【解析】解：选项A，，折叠后有一行两个面无法折起来，而且都缺少一个面，不能折成正方体．选项D可折成正方体．
故选：．
利用正方体及其表面展开图的特点解题．
本题考查展开图折叠成几何体的知识，注意掌握只要有“田”字格的展开图都不是正方体的表面展开图．
 9.【答案】
 【解析】解：

，
由题可知：，
，
故选：．
根据题意列出代数式进行化简即可求出答案．
本题考查整式的加减，解题的关键熟练运用整式的加减运算，本题属于基础题型．
 10.【答案】
 【解析】解：如图，

在甲图中，，则，故甲不符合题意；
在乙图中，过点作，
，
，
，，
，
，故乙符合题意；
在丙图中，，
，
，
，故丙符合题意，
故选：．
利用平行线的性质及三角形的内角和定理进行分析即可．
本题主要考查平行线的性质，解答的关键是熟记平行线的性质并灵活运用．
 11.【答案】
 【解析】【分析】
根据题意可得顺水速度为，逆水速度为，根据题意可得等量关系：以最大航速沿江顺流航行所用时间与以最大航速逆流航行所用时间相等，据此列出方程即可。
【解答】
解：设江水的流速为，则顺水速度为，逆水速度为。
根据题意，得 
故选D。  12.【答案】
 【解析】解：由作法得，，再过点作的平行线，最后过点作了的平行线得到点，
因为，，
所以四边形为平行四边形，
因为，
所以四边形为菱形．
故选：．
利用作法得到，，，，则根据菱形的判定方法可对各选项进行判断．
本题考查了作图复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行四边形的判定与性质和菱形的判定．
 13.【答案】
 【解析】解：根据图形，可知，，，，，
A、，所以，故本选项正确；
B、，所以，故本选项正确；
C、，故本选项正确；
D、，所以，，故本选项错误．
故选：．
根据，，的大小，进行判断即可．
本题考查的实数的大小比较，关键是利用好数轴来判断两个数的大小．
 14.【答案】
 【解析】解：，，
，
，
为整数且，
的值为：，
故选：．
根据题意可知与是两个连续整数，再估算出的值即可．
本题考查了估算无理数的大小，根据题意判断与是两个连续整数，再估算出的值是解题的关键．
 15.【答案】
 【解析】解：为的外心，
点为的中点，
设，
点的坐标为，点的坐标为，
，，
解得，，
点的坐标为，
，轴，
轴，
点坐标为．
故选：．
设，利用直角三角形的外心为斜边的中点，根据线段的中点坐标公式得到，，求出、得到点的坐标为，由于轴，轴，从而得到点坐标．
本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心；锐角三角形的外心在三角形的内部；直角三角形的外心为直角三角形斜边的中点；钝角三角形的外心在三角形的外部．也考查了坐标与图形性质．
 16.【答案】
 【解析】解：结论Ⅰ：如图，当点在的中点时，
、是半圆的三等分点，点在的中点，
，
，
，
四边形是圆内接四边形，
，
因此结论Ⅰ不正确；
结论Ⅱ：当点在上时，
当点在处时，不存在或，
因此结论Ⅱ不正确；
结论Ⅲ：当时，即，
因此有，
而，
点在上，
因此结论Ⅲ正确；
故选：．
根据圆周角定理、垂径定理以及圆内接四边形的性质逐项进行判断即可．
本题考查圆周角定理、垂径定理以及圆内接四边形，掌握圆周角定理、垂径定理以及圆内接四边形的性质是解决问题的前提．
 17.【答案】 
 【解析】解：，
的立方根是，
故答案为：；


．
故答案为：．
利用立方根的概念求解；
先化简二次根式，再合并同类二次根式
此题考查了立方根的求解和二次根式的计算能力，关键是能准确理解并运用以上知识并计算．
 18.【答案】 
 【解析】解：边形的外角和等于，
又一个边形的每一个外角都等于，
，
故答案为：；

一个边形的内角和是外角和的倍，
，
，
，
故答案为：．
根据多边形的外角和都等于得出即可；
根据题意得出即可．
本题考查了多边形的内角与外角，能熟记边数为的多边形的内角和和多边形的外角和斗等于是解此题的关键．
 19.【答案】， 
 【解析】解：当双曲线经过点时，，
当双曲线经过点时，，
点和点在双曲线的两侧，
的整数值为，；
解：由图象知，、、组成的点开口向上，；
A、、组成的二次函数开口向上，；
B、、三点组成的二次函数开口向下，；
A、、三点组成的二次函数开口向下，；
即只需比较、、组成的二次函数和、、组成的二次函数即可，
设二次函数为，
当抛物线过、、三点时，则，
解得；
当抛物线过、、三点时，则，
解得；
故的值最大时二次函数经过、、三点，且．
故答案为：．
分别将，代入中，可得对应的值，从而可解答；
比较任意三个点组成的二次函数，比较开口方向，开口向下，则，只需把开口向上的二次函数解析式求出即可判断．
本题考查了反比例函数的定义和二次函数与系数的关系，解本题的关键要熟练掌握二次函数和反比例函数的性质和待定系数法求函数的解析式．
 20.【答案】解：

；
，
五个有理数的和为，
．
 【解析】根据有理数的减法计算即可；
先求出这四个数的和，再根据五个有理数的和为即可得出的值．
本题考查了有理数的加减法，掌握减去一个数等于加上这个数的相反数是解题的关键．
 21.【答案】 
 【解析】解：一个夏威夷披萨调涨前的售价为元，会员调价前打八五折，
会员购买一个夏威夷披萨，涨价前的花费为元；
一个夏威夷披萨调涨后的售价为元，
会员调价后打九折，
会员购买一个夏威夷披萨，涨价后的花费为：元．
故答案为：；．

根据题意得：，
解得：，
答：一个夏威夷披萨调涨前的售价最高为元．
根据公告信息表示出调价前的花费和调价后的花费即可；
根据不等关系：调价后调价前，列出不等式，解不等式即可．
本题考查了一元一次不等式的应用和列代数式，正确理解题意，找出不等关系是解题的关键．
 22.【答案】                                             
 【解析】解：放入数字卡片后，四张卡片上数字的中位数和众数相同，
；
列表如下：  由表知，共有种等可能结果，其中小颖同学两次拿到卡片上的数字都是的有种结果，
所以小颖同学两次拿到卡片上的数字都是的概率为．
根据众数和中位数的概念求解即可；
由列表法表示出所有等可能结果，从中找到两次拿到卡片上的数字都是的结果数，利用概率公式计算可得．
本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出，再从中选出符合事件或的结果数目，然后根据概率公式求出事件或的概率．
 23.【答案】解：是，的中点，
，，
故四边形为平行四边形；
当时，如下图：

，，
，
即四边形为菱形，
，，
，，
，
四边形的周长为；
直线与线段旋转形成的扇形相切于点，
，
，，
，
，
线段扫过的扇形面积为
 【解析】根据对角线互相平分证四边形为平行四边形即可；
当时，则四边形为菱形，根据勾股定理求出边长即可；
求出旋转角度，再根据扇形面积公式计算即可．
本题主要考查圆的综合知识，熟练掌握平行四边形的判定，勾股定理，扇形的面积公式等知识是解题的关键．
 24.【答案】解：甲到达点之前，设，
由图象可知经过点，，
则，
解得：，
的解析式为；
由于过点和，设关于的函数解析式为，
则，
解得：，
关于的函数解析式为；
由知，当时，，
，
甲、乙之间的距离为；
设甲、乙两人出发分时，与点的距离相等，
甲到达点之前，两人与点的距离相等，
得，
解得：；
甲到达点之后，两人与点的距离相等，
得，
解得：，
两人与点的距离相等时，甲、乙两人出发的时间为分或分．
 【解析】根据图象设出函数解析式，用待定系数法求函数解析式即可；
分两种情列方程求解即可．
本题考查一次函数、一元一次方程的应用题，根据信息列函数解析式和一元一次方程是解题关键．
 25.【答案】解：把代入得：
，
解得，
把把代入得：
，
解得，
答：的值为，的值是；
如图：

由可得抛物线：与直线：，
设，则，
在线段上，


，
，
当时，取最大值，最大值为；
由得或，
，，
、的水平距离为，
当在左侧的直线上时，向左平移个单位长度得到点，此时线段与抛物线无公共点，
当在线段上不含时，向左平移个单位长度得到点，线段与抛物线只有一个公共点，
此时，
当在右侧的直线上时，若 ，则抛物线和线段交于抛物线的顶点，即时，线段与抛物线只有一个公共点，
综上所述，点的横坐标的取值范围是或．
 【解析】把代入和，即可得的值为，的值是；
设，则，可得，由二次函数性质可得最大值为；
由得，，可知、的水平距离为，分三种情况：当在左侧的直线上时，当在线段上不含时，当在右侧的直线上时，对线段与抛物线交点进行讨论．
本题考查二次函数综合应用，涉及待定系数法、平移变换及最大小值等知识，解题的关键是对的位置分类讨论．
 26.【答案】在 
 【解析】解：【发现】连接，如图，

为的直径，
，为圆的半径．
．
，
．
点在上．
故答案为：在；
当，
．
．
．
故答案为：；
【论证】，
．
，
．
．
在和中，
，
≌．
，．
，
．
【探究】】，
．
，
．
．
，
∽．
．
，是边，的中点，，
，．
．
，
．
．
【拓展】当点落在边上时，
过点作于点，过点作，交的延长线于点，如图，

，
．
，
．
．
在和中，
，
≌．
，．
在中，
，
设，则，
，
，
．
．
，．
．
，
．
．
．
设，则，
．
，
．
．
，
．
．
．
；
当点落在边的延长线上时，
过点作于点，过点作，交的延长线于点，如图，

同可得：，，，，
过点作于点，
为等腰直角三角形，
．
，，，
．
．
综上，当点落在平行四边形的边所在的直线上时，的长为或．
【发现】连接，说明点到圆心的距离等于半径即可；利用等弧对等弦得到，即可求得结论；
【论证】通过证明≌，即可证明结论成立；
【探究】利用相似三角形的判定与性质求得线段，，再利用勾股定理即可求解；
【拓展】利用分类讨论的方法分两种情况解答：】当点落在边上时，过点作于点，过点作，交的延长线于点，利用全等三角形的判定与性质和直角三角形的边角关系求得线段，，利用勾股定理即可求解；当点落在边的延长线上时，过点作于点，过点作，交的延长线于点，同的方法解答即可．
本题主要考查了矩形的性质，圆的有关性质，圆周角定理，点和圆的位置关系，三角函数值，全等三角形的判定与性质，相似三角形的判定与性质，平行四边形的性质，平行线的性质，勾股定理，直角三角形的性质，分类讨论的思想方法，利用类比的方法解答是解题的关键．