安徽省合肥市第一中学2022届高三下学期最后一卷文科数学试题

这是一份安徽省合肥市第一中学2022届高三下学期最后一卷文科数学试题，共26页。试卷主要包含了设集合，，则，若复数，数列的前项和，首项为1等内容，欢迎下载使用。
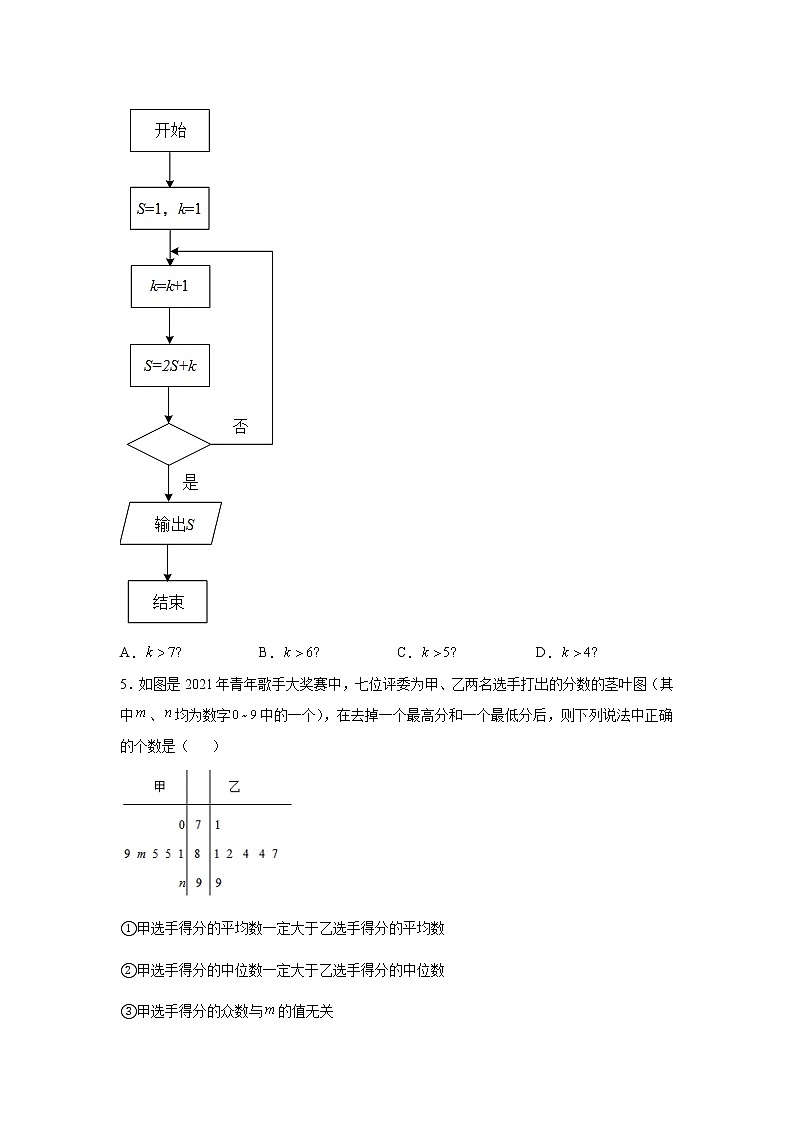
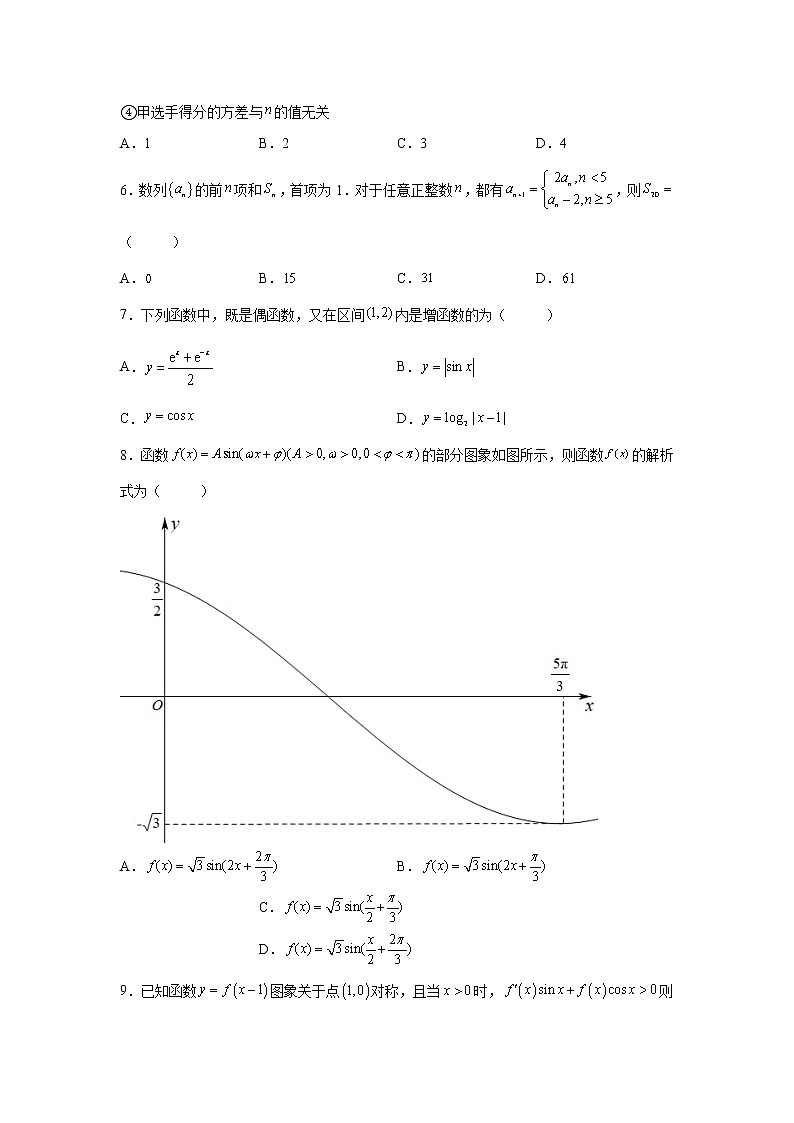
安徽省合肥市第一中学2022届高三下学期最后一卷文科数学试题第I卷（选择题）评卷人得分  一、单选题1．设集合，，则（       ）A． B． C． D．2．若复数（为虚数单位）是纯虚数，则实数（       ）A． B． C． D．3．若双曲线的一条渐近线经过点，则该双曲线的离心率为（       ）A． B． C． D．4．某程序框图如图所示，若输出的，则判断框内为A． B． C． D．5．如图是2021年青年歌手大奖赛中，七位评委为甲、乙两名选手打出的分数的茎叶图（其中、均为数字中的一个），在去掉一个最高分和一个最低分后，则下列说法中正确的个数是（       ）①甲选手得分的平均数一定大于乙选手得分的平均数       ②甲选手得分的中位数一定大于乙选手得分的中位数       ③甲选手得分的众数与的值无关       ④甲选手得分的方差与的值无关A．1 B．2 C．3 D．46．数列的前项和，首项为1．对于任意正整数，都有，则（       ）A． B． C． D．7．下列函数中，既是偶函数，又在区间内是增函数的为（       ）A． B．C． D．8．函数的部分图象如图所示，则函数的解析式为（       ）A． B． C． D．9．已知函数图象关于点对称，且当时，则下列说法正确的是（       ）A． B．C． D．10．首钢滑雪大跳台是冬奥史上第一座与工业旧址结合再利用的竞赛场馆，它的设计创造性地融入了敦煌壁画中飞天的元素，建筑外形优美流畅，飘逸灵动，被形象地称为雪飞天．中国选手谷爱凌和苏翊鸣分别在此摘得女子自由式滑雪大跳台和男子单板滑雪大跳台比赛的金牌．雪飞天的助滑道可以看成一个线段和一段圆弧组成，如图所示.假设圆弧所在圆的方程为，若某运动员在起跳点以倾斜角为且与圆相切的直线方向起跳，起跳后的飞行轨迹是一个对称轴在轴上的抛物线的一部分，如下图所示，则该抛物线的轨迹方程为（       ） A． B．C． D．11．某三棱锥的三视图如图所示，则该三棱锥的外接球的表面积为（       ） A． B． C．D．12．对于三次函数，若曲线在点处的切线与曲线在点处点的切线重合，则（       ）A． B． C． D．第II卷（非选择题）评卷人得分  二、填空题13．已知平面向量，满足，且的夹角为，则_____．14．我国古代认为构成宇宙万物的基本要素是金、木、水、火、土这五种物质，称为“五行”.古人构建了金生水、水生木、木生火、火生土、土生金的相生理论，随机任取“两行”，则取出的“两行”相生的概率是_______15．在正项等比数列中，，，记数列的前n项积为，，则n的最小值为______16．如图，点是正方体中的侧面内（包括边界）的一个动点，则下列命题正确的是___________(请填上所有正确命题的序号）．①满足的点的轨迹是一条线段；       ②在线段上存在点，使异面直线与所成的角是；       ③若正方体的棱长为1，三棱锥的体积最大值为；④存在无数个点，使得点到直线和直线的距离相等．评卷人得分  三、解答题17．在①，②，③这三个条件中任选一个，补充在下面的问题中，并解答问题．在中，内角A，B，C的对边分别为a，b，c，且满足________．(1)求C；(2)若 的面积为，D为AC的中点，求BD的最小值．18．为了了解A地区足球特色学校的发展状况，某调查机构得到如下统计数据：年份x20142015201620172018足球特色学校y（百个）0.300.601.001.401.70 （1）根据上表数据，计算y与x的相关系数r，并说明y与x的线性相关性强弱（已知：，则认为y与x线性相关性很强；，则认为y与x线性相关性一般；，则认为y与x线性相关性较弱）；（2）求y关于x的线性回归方程，并预测A地区2019年足球特色学校的个数（精确到个）.参考公式：，，，，，.19．如图，在四面体中，平面,，，是线段上一点，且. (1)证明：是的中点；(2)若，，求几何体的体积.20．已知椭圆的离心率，为椭圆的上顶点，为坐标原点，点满足.(1)求椭圆的标准方程；(2)过点的直线交椭圆于，两点，证明：.21．已知函数.(1)当时，试分析函数零点的个数；(2)若，，求的取值范围．22．在平面直角坐标系xOy中，已知曲线E经过点，其参数方程为 (α为参数)，以原点O为极点，x轴的非负半轴为极轴建立极坐标系.(1)求曲线E的极坐标方程；(2)若直线l交曲线E于点A，B，且OA⊥OB，求 的值．23．已知函数．(1)解不等式；(2)记函数的最小值为，若为正实数，且，求的最大值．
参考答案：1．D【解析】【分析】利用一元二次不等式的解法化简集合，再利用集合的交集运算即可得到结论．【详解】，，，故选：．【点睛】本题主要考查集合的基本运算，考查了一元二次不等式的解法，比较基础．2．A【解析】【分析】利用复数的运算法则和纯虚数的定义求解.【详解】为纯虚数，，故选：A．3．D【解析】【分析】由题意可求得，结合a,b,c之间的关系，即可求得离心率.【详解】由题意知，双曲线的一条渐近线经过点，故其斜率为 ，因为双曲线的渐近线方程为，即，即 ，解得，故选：D．4．C【解析】【详解】程序在运行过程中各变量值变化如下表：　K     S       是否继续循环循环前11　第一圈24是第二圈311是第三圈 426是第四圈 557是第五圈 6120否 故退出循环的条件应为k>5?本题选择C选项.点睛：使用循环结构寻数时，要明确数字的结构特征，决定循环的终止条件与数的结构特征的关系及循环次数．尤其是统计数时，注意要统计的数的出现次数与循环次数的区别．5．C【解析】【分析】计算出甲乙两人的得分的平均数,可比较大小,判断①;确定出两人的中位数即可判断②;由于m取值不同，则甲选手得分的众数就不同，判断③；因为是甲的最高分，被去掉，因此与方差无关，判断④.【详解】由题意，甲选手得分的平均数，乙选手得分的平均数，由于为数字中的一个,故,故命题①正确；无论为何值，甲选手得分的中位数一定是85，乙选手得分的中位数是84，故命题②正确；当时，甲选手得分的众数为81，85，当时，甲选手得分的众数为85，故命题③错误；因为是最高分，被去掉，故甲选手得分的方差与的值无关，故命题④正确；故选:C6．C【解析】【分析】根据题设递推关系，结合等差、等比数列的定义判断在、的性质，再应用分组求和，及等差、等比数列前n项和公式求和.【详解】由题设时，是首项为1，公比为2的等比数列，故且，所以，则，故时，是首项为14，公差为-2的等差数列，故且，所以.故选：C．7．A【解析】【分析】A.根据奇偶性的定义判断，利用导数法判断其单调性；B. 根据奇偶性的定义判断，利用正弦函数的性质判断其单调性；C. 根据奇偶性的定义判断，利用余弦函数的性质判断其单调性；D. 根据奇偶性的定义判断.【详解】A.因为，所以是偶函数，，在上单调递增，当时，，当时，，在上单调递增，故正确；B. ，所以是偶函数，易知在 上递增，在上递减，故错误；C. ，所以是偶函数，易知在上递减，故错误；D. 因为，所以，则不是偶函数，故错误；故选：A8．D【解析】【分析】由函数的最小值可求得的值，由结合的取值范围可求得的值，再由可求得的值，综合可得出结果.【详解】由图象可得，可得，，可得，由于函数在附近单调递减，且，，由图象可知，函数的最小正周期满足，可得，，则，所以，解得，，所以，，因此.故选：D.9．D【解析】【分析】本题有两个入手点：① 关于点对称；② 在上单调递增，然后以特殊值代入即可解决.【详解】由关于点对称可知，关于点对称，则为奇函数令，则为偶函数， 又时，，即则在上单调递增，则有即就是，故选：D10．C【解析】【分析】由题意可得到直线所在的方程和圆方程联立求得点的坐标，设所求抛物线方程，求导，根据导数的几何意义结合题意，可求得a,c,即得答案.【详解】由于某运动员在起跳点以倾斜角为且与圆相切的直线方向起跳，故,所以直线所在的方程为：，代入，解得 或 （舍，离y轴较远的点），所以点的坐标为.由于起跳后的飞行轨迹是一个对称轴在轴上的抛物线的一部分，故设抛物线方程为：，则，则由M点处切线斜率为1可得，，又，解得，所以该抛物线的轨迹方程为，即，故选：C.11．B【解析】【分析】由三视图得到三棱锥的直观图，易知 平面ABD， 平面BCD，设ABD和CBD的外心分别为，然后分别过作平面ABD和平面CBD的垂线，得到其交点即为该三棱锥外接球的球心求解.【详解】解：由三视图可知：该三棱锥，如图所示： 平面ABD，E是BD中点，平面BCD．且，BE=ED=1，，所以ABD为等边三角形，设ABD和CBD的外心分别为．分别过作平面ABD和平面CBD的垂线，其交点即为该三棱锥外接球的球心，连接，则，，该三棱锥的外接球的表面积为，故选：B．12．B【解析】【分析】由得，然后求得，由求得，设，由得及，再由得，解得后可得．【详解】设，，设，则，即……①又，即……②由①②可得，.故选：B.13．【解析】【分析】利用向量的运算性质求解.【详解】 故答案为：14．##0.5【解析】【分析】写出随机任取 “两行”共有多少种，再写出“两行”相生的可能情况，根据古典概型的概率计算求得答案.【详解】由题意得，随机任取“两行”共有金木、金水、金火、金土、木水、木火、木土、水火、水土、火土共10种，其中取出的“两行”相生的情况有金生水、水生木、木生火、火生土、土生金共5种，所以取出的“两行”相生的概率,故答案为：15．5【解析】【分析】由题意求出，继而求得的表达式，根据得到，解得，可得答案.【详解】设正项等比数列公比为q，由得，于是得，而，解得，因此，，，由得：，从而得：，而 ，解得，又，则n的最小值为5，故答案为：5.16．①③④【解析】【分析】根据线面垂直的判定定理可判断A;根据异面直线所成角的定义可找到异面直线与所成的角即为与所成角，表示出其正切值，求得其范围，可判断B; ，当点与点重合时，点到平面的距离最大，此时三棱锥体积最大，由此可求得三棱锥的体积最大值，判断C；由题意可知为到直线的距离，故可推得到点的距离等于到直线的距离，因此其轨迹为以为焦点，为准线的抛物线的一部分，可判断D.【详解】对于命题①，因为在平面中的射影为，当时，因为，，所以平面ABM，平面ABM所以成立，在正方形内， ,所以点在线段上，命题①正确．对于命题②，因为，所以异面直线与所成的角即为与所成角，设为 ，设，则，，所以，因为，所以，故符合条件的点不存在，命题②错误．对于命题③，当点与点重合时，点到平面的距离最大，此时三棱锥体积最大且三棱锥为棱长为的正四面体，其体积等于正方体的体积减去4个三棱锥的体积，为，命题③正确．对于命题④，因为平面，所以，即为到直线的距离．过点作，垂足为，则为到直线的距离,故到点的距离等于到直线的距离，其轨迹为以为焦点，为准线的抛物线的一部分，其上存在无数个点满足条件，故命题④正确．故命题①③④正确,故答案为：①③④【点睛】本题综合考查了空间的垂直关系以及异面直线的夹角以及棱锥的体积和空间几何体中的动点的轨迹问题，综合性较强，解答时要充分发挥空间想象能力，明确空间的点线面的位置关系，并能熟练进行相关的计算.17．(1)(2)2【解析】【分析】（1）选①，由正弦定理边化角，结合两角和的正弦公式化简可得，求得答案; 选②,由正弦定理边化角，结合同角的三角函数关系以及两角和的正弦公式化简可得，求得答案; 选③，由正弦定理边化角，结合两角差的余弦公式化简可得，求得答案; （2）利用三角形的面积公式可得，由余弦定理结合基本不等式可推出，即可求得答案.(1)选条件①．由可得，由正弦定理得， 因为，所以，所以，故，   又，于是，即，因为，所以. 选条件②．因为，所以由正弦定理及同角三角函数的基本关系式，得，   即，                    因为 ，所以，，又，故 ,所以，因为，所以 选条件③．在 中，由正弦定理得 ，又，所以   ,            所以，所以，即，又，所以 ；(2)由题意知，得，由余弦定理得，当且仅当且，即时取等号，所以BD的最小值为2.18．（1），y与x线性相关很强；（2）y=0.36x-724.76，208个.【解析】【分析】（1）求出，代入公式计算即可；（2）根据公式求出回归方程，根据回归方程计算预测结果.【详解】（1），所以y与x线性相关很强；（2），，y关于x的线性回归方程y=0.36x-724.76，当x=2019时，y=2.08，即A地区2019年特色学校208个.19．(1)证明见解析(2)【解析】【分析】（1）取的中点，连接，根据题意可得，根据线面垂直的性质可得，从而可得，再根据线面垂直的判定定理可得平面，再证明即可得证；（2）利用勾股定理证明，再根据线面垂直的判定定理可得平面，即可求得棱锥的高，求出底面积，再根据棱锥的体积公式即可得解.(1)证明：取的中点，连接，由，得，又，所以,又平面，平面，所以，所以，又，，所以平面，因为平面，所以,所以，又为的中点，所以是的中点；(2)解：由，，故，所以，因为平面，平面，所以，又，所以平面，是的中点，所以到平面的距离为，由（1）得，，所以四棱锥的体积为.【点睛】20．(1)(2)证明见解析【解析】【分析】（1）由离心率可得a与b的关系，再根据，得b的值，从而得到椭圆的标准方程；（2）根据要证的结论分析转化为证，联立方程即证.(1)，又，解得，.所以椭圆的标准方程为.(2)由题意知，直线斜率存在，设直线的方程为：，设，.要证：，只要证：，即证：，只要证：.联立直线和椭圆的方程消去得，∴                                                                                所以原命题成立.21．(1)函数在上有且只有一个零点(2)【解析】【分析】（1）根据函数的单调性和零点存在定理可证；（2）令，则等价于，转化为函数的最小值大于0的问题.(1)当时，函数，由，解得或；由，解得.所以函数在区间和上单调递增，在区间上单调递减.又，；所以函数在上有且只有一个零点(2)令，则等价于．若，则，在区间上恒成立，在区间上单调递增，故，符合条件．若，则当时，；当时，．故在区间上单调递减，在区间上单调递增，则不符合条件．若，则对恒成立，在区间上单调递减，故，不符合条件．综上所述，的取值范围为.22．(1)(2)【解析】【分析】（1）将点，代入曲线E的方程，求出，可得曲线E的普通方程，即可求曲线E的极坐标方程；（2）利用点的极坐标，代入极坐标方程，化简，即可证明结论．(1)将点代入曲线E的方程，得解得，所以曲线的普通方程为，极坐标方程为.(2)不妨设点的极坐标分别为则即，，即.23．(1)(2)8【解析】【分析】（1）根据，分，，求解；（2）先求得函数的最小值，进而得到，利用基本不等式求解.(1)解：，则等价于或或，解得或或，所以不等式的解集为；(2)由，得，，且为正实数，，当且仅当，又，即时等号成立，的最大值为．