2022年山东省泰安市岱岳区中考二模数学试题(word版含答案)

2022年山东省泰安市岱岳区中考二模数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．－5的倒数等于（       ）

A．－5 B．5 C． D．

2．下列运算正确的是（       ）

A． B．

C． D．

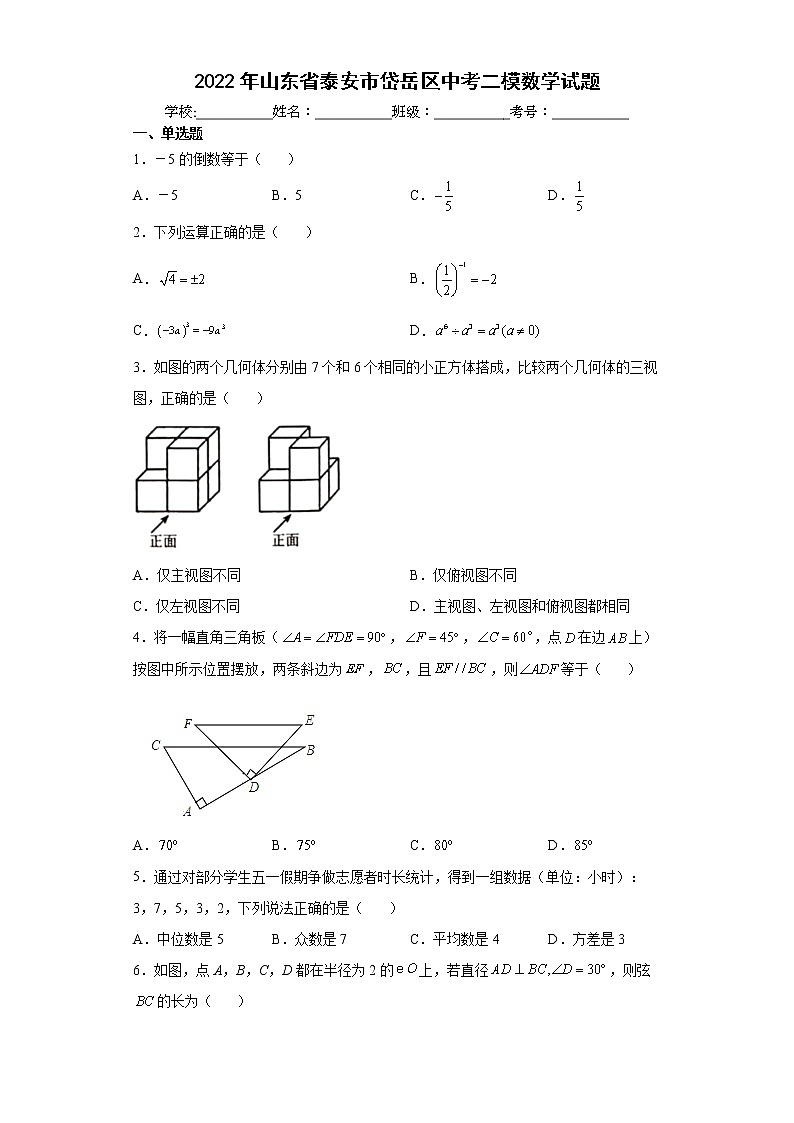
3．如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是（       ）

A．仅主视图不同 B．仅俯视图不同

C．仅左视图不同 D．主视图、左视图和俯视图都相同

4．将一幅直角三角板（，，，点在边上）按图中所示位置摆放，两条斜边为，，且，则等于（       ）

A． B． C． D．

5．通过对部分学生五一假期争做志愿者时长统计，得到一组数据（单位：小时）：3，7，5，3，2，下列说法正确的是（       ）

A．中位数是5 B．众数是7 C．平均数是4 D．方差是3

6．如图，点A，B，C，D都在半径为2的上，若直径，则弦的长为（       ）

A．4 B． C． D．

7．关于的不等式组的解集为，那么的取值范围为（     ）

A． B． C． D．

8．将二次函数沿x轴对折，再向右平移1个单位，得到的抛物线必定经过（       ）

A． B． C． D．

9．如图所示，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C，连接BC，若，则等于（       ）

A． B． C． D．

10．已知二次函数图象的对称轴为，其图象如图所示，现有下列结论：①；②；③；④；⑤．正确的是（       ）

A．①③ B．②⑤ C．③④ D．④⑤

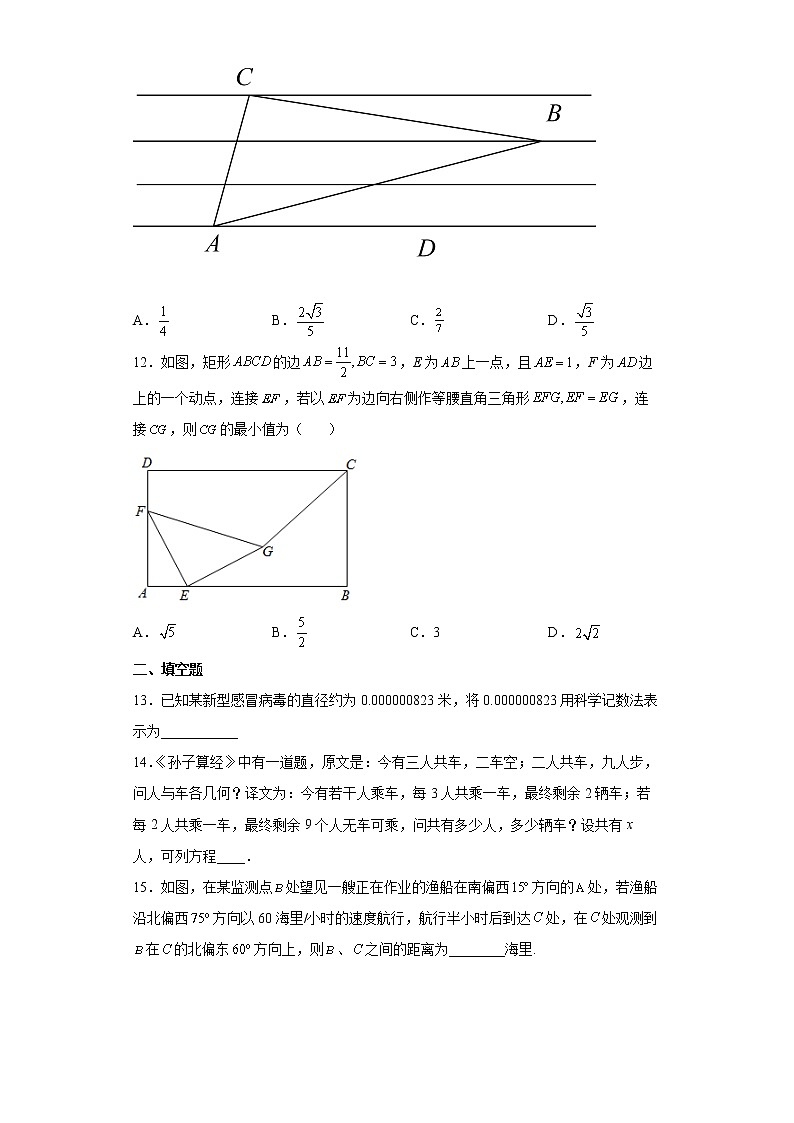
11．如图，有等间距的四条平行线且相邻两条平行线间的距离是3，含角的直角三角板三个顶点A、B、C，分别在平行线上，则（       ）

A． B． C． D．

12．如图，矩形的边，E为上一点，且，F为边上的一个动点，连接，若以为边向右侧作等腰直角三角形，连接，则的最小值为（       ）

A． B． C．3 D．

二、填空题

13．已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为___________

14．《孙子算经》中有一道题，原文是：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车；若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有x人，可列方程____．

15．如图，在某监测点处望见一艘正在作业的渔船在南偏西方向的处，若渔船沿北偏西方向以60海里/小时的速度航行，航行半小时后到达处，在处观测到在的北偏东方向上，则、之间的距离为________海里.

16．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB＝60°，FO＝FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE＝EF；④．其中正确结论的个数是（填写序号）________．

17．如图，扇形中，，，是的中点，交于点，以为半径的弧交于点，则图中阴影部分的面积是______．

18．设计师构思了一地标性建筑，如图，在平面直角坐标系中，有两反比例函数和，依次向上如图所示作一内角为的菱形，使顶点分别在y轴和函数图象上，请写出的坐标____________．

三、解答题

19．先化简，再求值：，其中，满足．

20．为了解疫情期网学生网络学习的学习效果，东坡中学随机抽取了部分学生进行调查．要求每位学生从“优秀”、“良好”、“一般”、“不合格”四个等次中，选择一项作为自我评价网络学习的效果现将调查结果绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

（1）这次活动共抽查了_________________人．

（2）将条形统计图补充完整，并计算出扇形统计图中，学习效果“一般”的学生人数所在扇形的圆心角度数．

（3）张老师在班上随机抽取了4名学生，其中学习效果“优秀”的1人，“良好”的2人，“一般”的1人，若再从这4人中随机抽取2人，请用画树状图法，求出抽取的2人学习效果全是“良好”的概率．

21．如图，已知反比例函数的图象与直线相交于点，．

(1)求出及的表达式；

(2)在x轴上有一点P使得的面积为18，求出点P的坐标．

22．决定购买A、B两种树苗对某路段道路进行绿化改造，己知购买A种树苗8棵，B种树苗3棵，需要950元．若购买A种树苗5棵，B种树苗6棵，则需要800元．

(1)求购买A、B两种树苗每棵各需要多少元？

(2)考虑到绿化效果和资金周转，购进A种树苗不能少于50棵，且用于购买这两种树苗的资金不能超过7650元．若购进这两种树苗共100棵，若种好一棵A种树苗可获工钱30元，种好一棵B种树苗可获工钱20元，种好这100棵树苗，怎样购买所付的种植工钱最少？最少工钱是多少元？

23．如图，正方形中，M是其内一点，，将绕点B顺时针旋转至，连接、、，延长交与点E，交与点G．

(1)在图中找到与相等的线段，并证明．

(2)求证：E是线段的中点．

24．物线经过点和点，与y轴交于点C．

(1)求该抛物线的函数表达式；

(2)①如图1，点P是第三象限抛物线上的动点，过点P作轴于点D，作轴于点E，当四边形周长最大时，求的值；

②如图2，该抛物线上是否存在点P，使得？若存在，请求出所有点P的坐标；若不存在，请说明理由．

25．（1）如图1，在中为直径，C为上一点，D为上一动点，E为上一点，

①求证：；

②若半径为5，，当D运动至中点时，如图2，求的长．

（2）若三角形形状发生变化，，点D为上的动点，且，求的值．

参考答案：

1．C

2．D

3．D

4．B

5．C

6．D

7．C

8．A

9．B

10．D

11．D

12．B

13．8.23×10-7

14．

15．

16．①③④

17．

18．

19．;-6.

20．（1）200；（2）图见解析，；（3）

21．(1)；

(2)或

22．(1)A100元，B50元

(2)购进A种树苗50棵，B种树苗50棵所付工钱最少，最少工钱为2500元

23．(1)，证明见解析

(2)证明见解析

24．(1)

(2)①6；②或

25．（1）①证明见解析；②；（2）90