初中数学19.2.3一次函数与方程、不等式图文ppt课件

这是一份初中数学19.2.3一次函数与方程、不等式图文ppt课件，共21页。PPT课件主要包含了导入新课，x＝2，二元一次方程，一次函数，x+y5，到我这里来，函数图象如右图所示，从“函数值”看，从“函数图象”看，求不等式的解等内容，欢迎下载使用。

1．已知函数y＝kx＋b(k≠0)的图象与y轴交点的纵坐标为－2，且当x＝2时，y＝1，那么此函数的解析式为__________．
2．一次函数y＝x－2与x轴交点的坐标是_______，一元一次方程x－2＝0的解是_______.
今天数学王国搞了个家庭Party，各个成员按照自己所在的集合就坐，这时来了“x+y=5”.
这是怎么回事？ x+y=5应该坐在哪里呢？
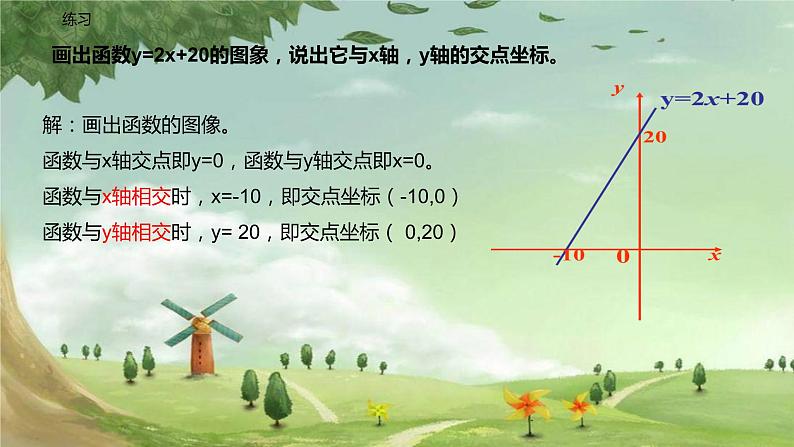
画出函数y=2x+20的图象，说出它与x轴，y轴的交点坐标。
解：画出函数的图像。函数与x轴交点即y=0，函数与y轴交点即x=0。函数与x轴相交时，x=-10，即交点坐标（-10,0）函数与y轴相交时，y= 20，即交点坐标（ 0,20）
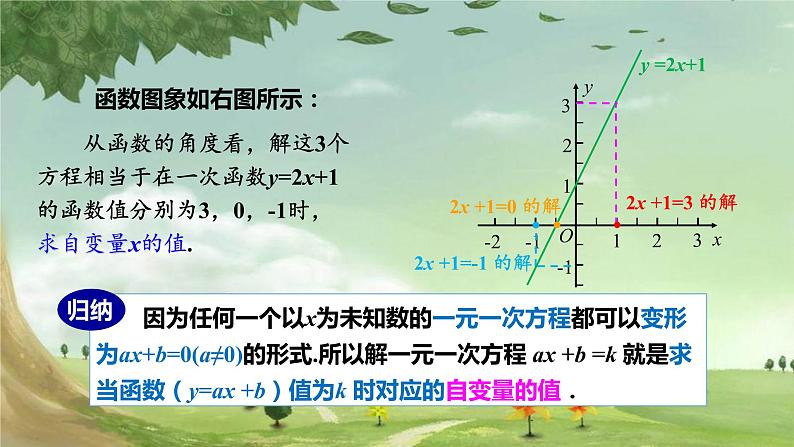
从函数的角度看，解这3个方程相当于在一次函数y=2x+1的函数值分别为3，0，-1时，求自变量x的值.
因为任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式.所以解一元一次方程 ax +b =k 就是求当函数（y=ax +b）值为k 时对应的自变量的值．
2x +1=-1 的解
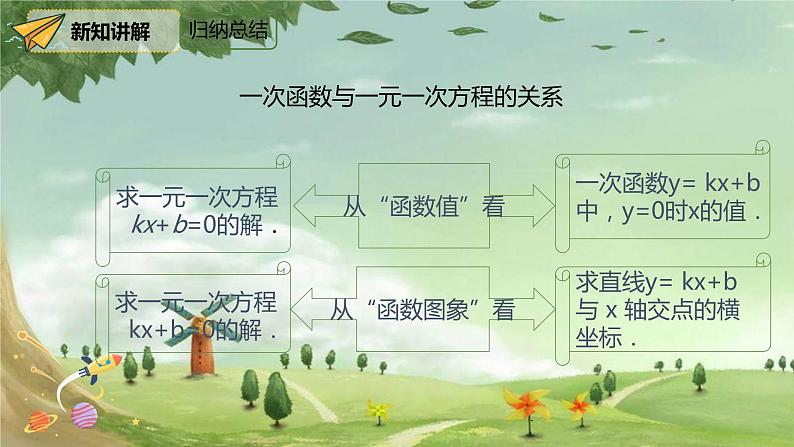
求一元一次方程 kx+b=0的解．
一次函数与一元一次方程的关系
一次函数y= kx+b中，y=0时x的值．
求直线y= kx+b与 x 轴交点的横坐标．
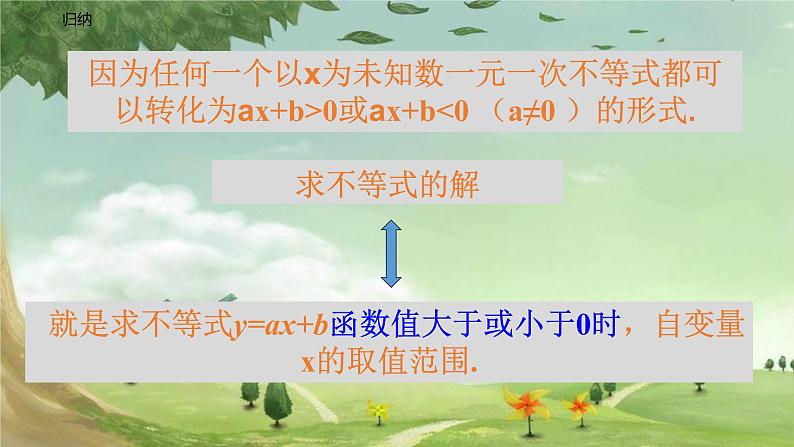
因为任何一个以x为未知数一元一次不等式都可以转化为ax+b>0或ax+b<0 （a≠0 ）的形式.
就是求不等式y=ax+b函数值大于或小于0时，自变量x的取值范围.
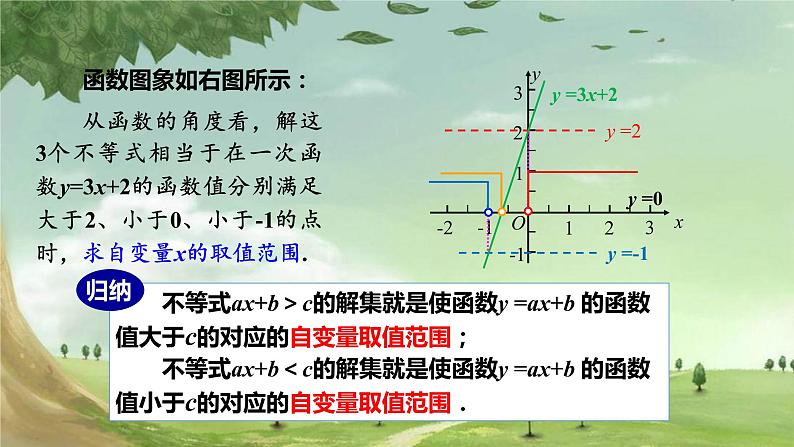
从函数的角度看，解这3个不等式相当于在一次函数y=3x+2的函数值分别满足大于2、小于0、小于-1的点时，求自变量x的取值范围.
　　不等式ax+b＞c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围；　　不等式ax+b＜c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围．
解法3：速度y（单位：米/秒）是时间x（单位：秒）的函数，y=2x+5
由右图可以看出当y =17时，x=6.
函数的角度看解二元一次方程组
1号探测气球从海拔5 m 处出发，以1 m/min 的速度上升。与此同时，2号探测气球从海拔15 m 处出发，以0.5 m/min 的速度上升。两个气球都上升了1 h。1）用式子分别表示两个气球所在位置的海拔y（单位：m）关于上升时间x（单位：min）的函数关系；
气球上升时间x满足0≤x≤60气球1 海拔高度：y = x +5气球2 海拔高度：y =0.5x +15
　　二元一次方程组的解就是相应的两个一次函数图象的交点坐标．
用一次函数图象解释上述问题，在直角坐标系中画出一次函数y =x+5与y =0.5x+15的图象.
如图，已知直线y=kx+b与x轴交于点(- 4,0)，则当y>0时，x的取值范围是（ ） A.x>-4 B. x>0 C. x<-4 D. x<0
一般因为每个含有未知数x和y的二元一次方程，都可以写成y=kx+b（k≠0，k，b为常数 ）的形式。所以每个这样的方程都对应一个一次函数，即对应一条直线。
都是这个二元一次方程的解
直线上每个点的坐标（x，y）
例2　对照图象，请回答下列问题：(1)当x取何值时，2x－5＝－x＋1?(2)当x取何值时，2x－5＞－x＋1?(3)当x取何值时，2x－5＜－x＋1?
解：(1)由图象可知，直线y＝2x－5与直线y＝－x＋1的交点的横坐标是2，∴当x＝2时，2x－5＝－x＋1；(2)由图象可知，当x＞2时，2x－5＞－x＋1.(3)由图象可知，当x＜2时，2x－5＜－x＋1.
思考1：一次函数与二元一次方程有什么关系？
根据下列一次函数的图像，直接写出下列不等式y>0和y<0的解集。
由图可知，当3x+6>0时，即x>-2时y>0;当3x+6<0时，即x<-2时y<0 。
由图可知，当-x+2>0时, 即x<2时y>0;当-x+2<0时，即x>2时y<0 。
1．教材P98　练习．2．已知函数y＝kx＋b，当x＞5时，y＜0；当x＜5时，y＞0，则y＝kx＋b的图象必经过点(　　)　A．(0，5)　　　B．(5，0)　　　C．(－5，0)　　　D．(0，－5)
3．若直线y＝3x－1与y＝x－k的交点在第四象限，则k的取值范围为_____________．
4.如图，一次函数y=ax+b与y=cx+d的图象交于点P，则方程组 的解是多少？
一般地，任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数，且k≠0)的形式，所以每个二元一次方程都对应一个一次函数，也对应一条直线．
方程组的解 对应两条直线交点的坐标.