苏教版六年级下册1. 数与代数随堂练习题

苏教版版数学六年级下册第七单元单元学习力提升练习卷

          总复习数与代数2：式与方程、正比例和反比例

哈喽，孩子们好！

美好的一天开始啦！提高学习力才能达到真正意义上的减负！学习力分为三个阶段，从知识层面的接受，到技能层面的模仿，再到知识层面的内化。 “磨刀不误砍柴工”,只有打好能力基础,才能高效学习。让我们以解决问题为目的，以学习力为帆，以内驱力为桨，展开新的征程。提升学习力，我能行！

名师指导：

例1.已知长方形内的几个小长方形的面积（如图），？　 　    。

例2.一个平行四边形被两条线段分割成四个平行四边形（如图），其中甲、乙、丙

的面积分别是25平方米，20平方米和30平方米，那么丁的面积是　 　平方米．

                 例1                       例2

   例3：（拓展题）蜡烛每分钟燃烧的长度一定，点火10分钟，蜡烛长度是14厘米，燃烧20分钟时再量，蜡烛长是8厘米，则蜡烛未点燃前是　    　厘米．

例4：小伟看一本科技书，已经看的页数与未看页数的比是，如果再看20页，正好看完这本书的，这本书共有多少页？

例5：在比例尺是的地图上，量得市到市的距离是，两辆车分从两市同时出发，相向而行．快车每时行驶，慢车每时行驶，多长时间后两车相遇？

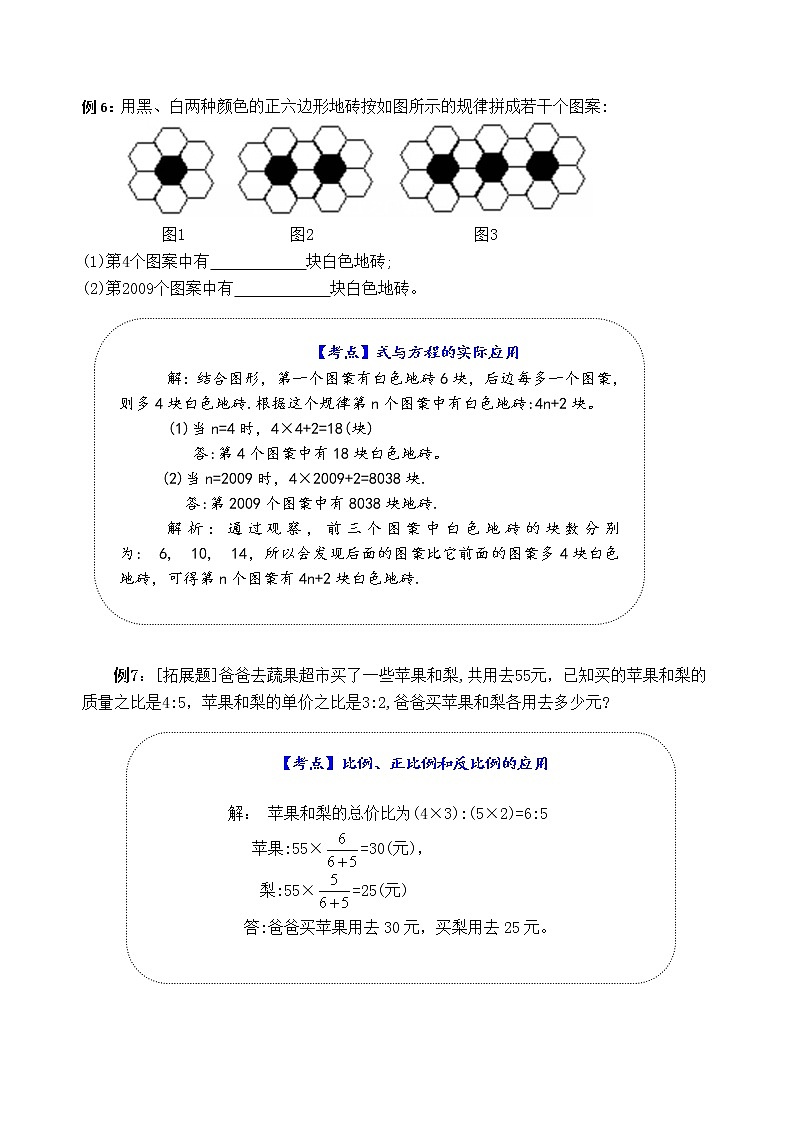
例6：用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
 

图1             图2                    图3
(1)第4个图案中有            块白色地砖;
(2)第2009个图案中有            块白色地砖。
 

例7：[拓展题]爸爸去蔬果超市买了一些苹果和梨,共用去55元，已知买的苹果和梨的质量之比是4:5，苹果和梨的单价之比是3:2,爸爸买苹果和梨各用去多少元?

六年级数学下册第七单元学习力提升练习卷

一、认真读题,准确填写。

1．　　　　　　　　（小数）

2．用含有字母的式子表示下面数暈关系．

（1）小明买了个笔记本，每本元，找回1.5元，小明付给售货员　　元．

（2）乐乐从家步行到学校，5分钟走米，他平均1分钟走 　　 米．

3.学校食堂买来吨大米，每天吃去0.5吨，吃了天，还剩 　　 吨．如果，，那么剩下　　吨．

4．在一个比例里，已知两个外项互为倒数，其中一个内项是最小的质数，另一个内项是　　．

5．已知、、三种量的关系是，如果一定，那么和成　 　比例关系，如果一定，和成　 　比例关系．

6.（拓展题）在表中，如果和成正比例，那么“？”处填　　，

如果和成反比例，那么“？”处填　　．

7．若在□里填上一个数，使方程与方程有相同的解，则□里应填的数是　　   。

8．某商品进价为200元，按标价的九折卖出后，利润率为，求标价．设标价为，列出方程　　．

9．3个连续自然数，中间的一个数是，这3个数的和是　 　，这3个数的平均数是　 　．

10．如果，那么和成　 　比例；如果，那么和成　 　比例．

11．在一个减法算式中，被减数、减数、差三个数的和是168，减数与差的比是，减数是　 　．

12．三个分数的和是，它们的分母相同，分子比为，其中最小的分数是　　．

13．某校32位男生进行跳远测试，其中合格人数是未合格的人数的，如果设未合格人数是人，那么合格人数是 　　 人，并在括号内列出等量关系　　　　               ．

14．在一张比例尺为的地图上量的、两城市之间的距离为4厘米，那么在的地图上，两城市之间的距离为　　        ．

15.爸爸手机的开机密码是一个六位数:☆△△☆☆△,其中相同的图形代表相同的数字。已知☆+△=14,☆:△=4:3,这个开机密码是         。

16．（拓展）根据如图，我能列出方程　　          ，并求出小球的重量是 　　 克．

                  第16题                      第17题

17.如图，一长方形被一条直线分成两个长方形，这两个长方形的宽的比为1:3，若阴影三

角形面积为1平方厘米，则原长方形面积为　 　  平方厘米．

18.如下图所示,一张桌子可以坐4人，两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人。像这样拼起来,5张桌子可以坐　 　  人,　 　   张桌子可以坐48人。

19.如右图,小明用小棒搭房子，，他搭3间房子用了13根小棒。照这样，搭10间房子要用　 　   根小棒;搭n间房子要用　 　   　 　   根小棒 。
 

20.[拓展题]请仔细观察下列各图中直角三角形的个数与正方形的扫码教你做个数,看看有什么规律，根据这个规律把下表填写完整。
     

21.用黑、白两种颜色的正六边形地砖按如图所示的规律拼成若干个图案:
 

图1         图2              图3
(1)第4个图案中有            块白色地砖;
(2)第200个图案中有            块白色地砖。
二、仔细推敲,准确判断。(对的在括号里画“√”,错的画“×”)

1.已知，则的倒数是．                              (     )

2.方程一定是等式，等式却不一定是方程．                       (     )

3.已知，则的值是1．                      (     )

4.修一条路，已修的与未修的长度成反比例关系                   (     )

5.，方程的两边同时加，方程的解不变．               (     )

6.因为，所以除法、分数、比的意义相同              (     )

7.如果和成正比例，和成反比例，那么和一定成反比例．  (     )

8.读作18比10，其中18是比的前项，10是比的后项．       (     )

9.一长方形的长比宽的4倍多2厘米，长是14厘米，若设宽为厘米，则列方程为．                                                (     )                                         

10.走同一段路，小明用了10分钟，小红用了12分钟，小明和小红的走路速度之比是。                                                                      (    )

三、反复比较，精挑细选。

1.从甲桶中取出的油倒人乙桶,这时两桶油的质量相等,原来甲,乙两桶中油的质量比是
(    ).

A.6:5              B.5:3             C.4 :5         D.7 :5

2.盒子里有80枚白子和50枚黑子。每次取走3枚白子，同时放人3枚黑子,像这样取放(   )次后,白子和黑子的数量正好相等。
A.5               B.4                C.3             D.2

3.甲、乙、丙三数之比为，这三个数的平均数为24，则甲数是　　

A．8 B．16 C．32 D．64

4.一个长，宽的长方形按放大，得到的图形的面积是　　．

A．32 B．72 C．128

5.在比例尺是的地图上，量得、两港距离为，一艘货轮于上午7时出发，以每小时的速度从港开向港，到达港的时间是　　。

A．22时 B．23时 C．21时

6.如右图所示，一个大长方形被两条线段分成四个小长方形．如果其中图形、、的面积分别是、和那么阴影部分的面积为　　．

A．1 B． C． D．

7.已知甲的等于乙的，甲的等于乙的　　

A． B． C． D．

8.一杯的鲜牛奶大约含有钙质，占一个成年人一天所需钙质的．设一个成年人一天大约需要钙质，下列方程中符合题意的是　　

A．    B．     C．    D．

9.小明今年6岁，他的祖父72岁，几年后，小明的年龄是他祖父的．设年后小明的年龄是他祖父的，则列方程正确的是　　。

A． B． 

C． D．

10.如下左图,一面装饰墙的墙面是由两种颜色的瓷砖贴成的。灰与白两种瓷砖面积的比是(      ）。
  A．4:3 B．5:4 

C．5:3 D．4:3

四、认真审题，谨慎计算。（怎样简便就怎样算）

1.化简比．

米：45分米 500厘米：5千米 1.2小时：40分

2.解方程或比例．

（1） （2） （3）

（4） （5） （6）

五、细心观察，动手实践。

1.下面每个方格的边长表示1厘米．

（1）画一个长方形，周长是24厘米，长和宽的比是．

（2）画一个长方形，面积是24平方厘米，长和宽的比是．

2.如图方格中小正方形的边长是1厘米．将方格中的梯形划分成、、三个三角形，使它们的面积比为．

（1）分别求出、、三个三角形的面积．

（2）在如图的梯形中画出、、三个三角形，并标出、、．

3.下面的方格纸中每一小方格的面积表示1平方厘米，请根据要求填空或作图．

（1）线段的长是　 　厘米，在线段上取一点，使（标出点）．

（2）以为圆心，为半径在上图中画一个圆，这个圆的周长是　 　．

（3）将上图中的三角形先向上平移4格，再向右平移　 　格，使平移后三角形的一个顶点位置在上．请画出平移后的图形．

（4）请画出上图中五边形绕点逆时针旋转后的图形，如果将这个五边形的每条边都按照放大，那么放大后的五边形的面积是原来五边形面积的　 　倍．

六、活用知识，解决问题。

1.壮壮和爷爷今年分别多少岁？（列方程解决问题）

2.“双十一”期间，一种工具书降价后是每本96元．

（1）这本工具书的原价是多少元？（列方程解答）

（2）这种工具书实际是打几折出售的？

3.春雨服装加工厂4天加工了2400套服装，照这样计算，再加工5天就可以完成任务．春雨服装加工厂共加工多少套服装？（用比例解答）

4.买来一批煤，计划每天烧吨，可烧20天；实际每天比原来节约，这样可以烧多少天？（用比例解答）

5.某区举行数学竞赛，试题共有10道，每做对一题得8分，每做错一题倒扣5分，李强最终得41分，他做对了多少道题？（用方程解）

6.某品牌数码相机进行促销活动，打九折．在此基础上，商场又返还售价的现金．王老师买了一部相机花了1710元．这种数码相机原价是多少元？

（1）写出数量关系式：                                   ．

（2）列出与等量关系对应的方程并解答．

七、拓展延伸，发散思维。

1.有两桶油，甲桶比乙桶少15升，现在把乙桶油的倒入甲桶，这时甲桶油比乙桶油多5升。原来两桶油各有多少升?

2.在比例尺是1:5000000的地图上量得甲、乙两地间的距离是9.6cm,一辆客车和一辆货车分别从甲、乙两地出发,4小时后相遇,已知客车与货车的速度比是3:2,客车和货车的速度分别是多少?
 

3. 甲、乙两队原来人数的比是7:3,从甲队调出一些人到乙队后，两队人数的比是3:2，乙队现在有120人。从甲队调出多少人到乙队?
    

4. 赵亮同学想利用影长测量学校旗杆的高度。他在某一时刻立一根1米长的标杆,测得其影长为1.2米，同时旗杆AB投影一部分 在地面上，另一部分在某建筑物的墙上，分别测得其长度为9.6米和2米(如图)。求旗杆的高度。
         

5.甲、乙两个修路队人数的比是7:3。如果从甲队派30人到乙队，则甲、乙两队人数的比是3:2。甲、乙两个修路队原来各有多少人? 
 

答案是咱无声的老师

参考答案

一、

1．20，2，80，0.8．

2．，．

3．，18．

4．．

5．反、正．

6．，．

7．3．

8．．

9．4、9．

10．正，反．

11．36．

12．．

13．，合格人数未合格的人数．

14．12.5．

15.866886

16．；x=85

17.    1×2÷=

18.解：一张桌子可以坐4人;拼2张桌子可以坐4+2×1=6人;拼3张桌子可以坐4+2×2=8人;故n张桌子拼在一起可以坐4+2(n-1)=2n+2.当2n+2=48时，n=23;当n=5,2n+2=12.
故答案为:12\23
解析:观察摆放的桌子，不难发现:在1张桌子坐4人的基础上，多1张桌子，多2人.则有n张桌子时，有4+2(n-1)=2n+2人;由此即可计算当2n+2=48人时，求得桌子张数n的值.

19. 41  4n+1

20. 12  16  4(n-1 )

解析：通过观察，前三个图案中白色地砖的块数分别为: 6, 10, 14，所以会发现后面的图案比它前面的图案多4块白色地砖，可得第n个图案有4n+2块白色地砖.
解：(1)由第1个图案可知，白色地砖有6块，由第2个图案可知，白色地砖有6+4=10块,由第3个图案可知，白色地砖有10+4=6+4×2=14块,根据规律推测第4个图案，白色地砖有14+4=6+4×3=18块。故第4个图案中有18块白色地砖。
(2)总结规律可知，第n个图案中白色地面砖有6+4(n-1)=(4n+2)块,
当n=200时，(4n+2)=802 ,故第200个图案中有802块白色地砖。
二、   

三、

1.B   2.A   3.A   4.C    5.A    6.C   7.B   8.C    9.B    10.C

四、

1.解：（1）；

（2）；

（3）；

（4）米：45分米分米：45分米；

（5）500厘米：5千米厘米：500000厘米；

（6）1.2小时：40分分：40分．

2.解：（1）

（2）

（3）

（4）

（5）

（6）

五、

1.解：（1）长与宽的和为：（厘米）

宽为：（厘米）   长为：（厘米）

（2）（平方厘米）    所以长和宽分别是6厘米和4厘米；

作图如下：

2.解：（1）

（平方厘米）

（平方厘米）

（平方厘米）

（平方厘米）

（平方厘米）

（2）三角形各定点在格点上，所以：

三角形：底1厘米，高4厘米，面积：（平方厘米）

三角形：底2厘米，高4厘米，面积：（平方厘米）

三角形：底3厘米，高4厘米，面积：（平方厘米）

如图所示：

3.解：（1）每一小方格的面积表示1平方厘米，则其边长为1厘米，

观察图形可得线段的长是5厘米，（厘米）如图所示：

（2）如图所示：

（厘米）

答：这个圆的周长是12.56厘米．

（3）将上图中的三角形先向上平移4格，再向右平移10格，使平移后三角形的一个顶点位置在上．如图所示：

（4）如图所示：

答：放大后的五边形的面积是原来五边形面积的2.25倍．

故答案为：5；12.56厘米；10；2.25．

六、

1.解：设壮壮今年岁，则爷爷今年岁．

爷爷：（岁

答：壮壮和爷爷今年分别10岁和70岁．

2.解：（1）设原价是元，则

答：原价是120元．

3.解：设共加工套服装，由题意得，

      ．

答：春雨服装加工厂共加工5400套服装．

4.解：设这样可以烧天，

答：这样可以烧25天．

5.解：设他做对了道题，

答：他做对了7道题．

6.解：（1）数量关系式：实际所花钱数原价．

（2）设数码相机的原价为元，

九折

答：这种数码相机的原价是2000元．

故答案为：实际所花钱数原价．

七、

1.解:设原来乙桶油有x升。
x-15+x=(1-)x+5
      x=50
  50-15=35 (升)
答:原来甲桶油有35升，乙桶油有50升。
2.9.6÷=48000000(cm)=480(km)
解:设货车的速度是x千米/时，则客车的速度是x千米/时。
（x+x)×4=480   x=48      2×48=72(千米/时)
答:客车的速度是72千米/时，货车的速度是48千米/时。
3.120-120÷×=30(人)  答:从甲队调出30人到乙队。

4. 9.6×1÷1.2+2=10(米)
答:旗杆的高度是10米。

5.30÷（-）=300 (人)
甲队: 300×=210(人)    乙队:300×=90(人)
答:甲修路队原来有210人，乙修路队原来有90人。