






2020-2021学年19.3 课题学习 选择方案教课内容ppt课件
展开利用一次函数解实际问题,首先要建立函数模型,求函数解析式.求函数解析式可以根据题目中所给出的两个变量之间的关系列出函数解析式,也可以根据两个变量之间满足的图象关系用待定系数法求函数解析式.其次,把已知自变量的值代入函数解析式中求函数值或把已知函数值代入函数解析式中求自变量的值,从而解决实际问题.注意:对于分段函数容易忽略自变量的取值范围而导致错误.
建立一次函数模型解实际应用中的方案问题
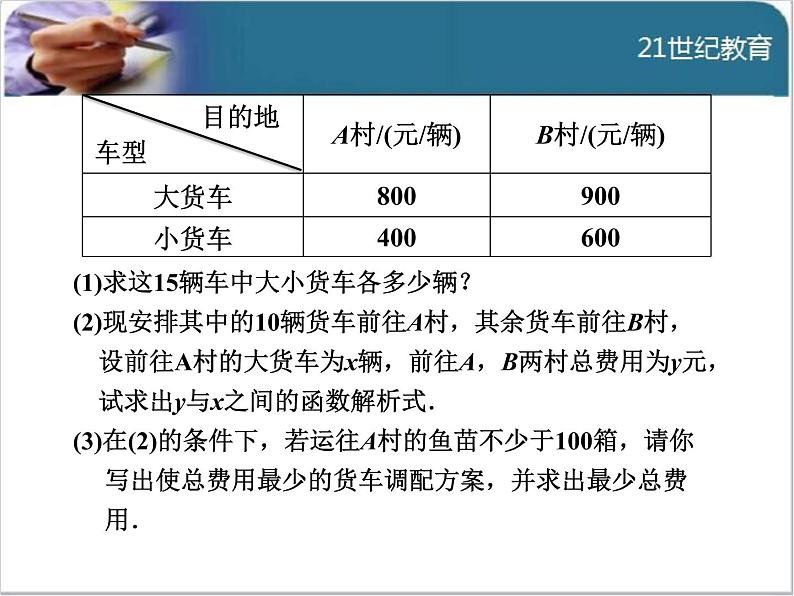
1. (2015·广安)为了贯彻落实市委市政府提出的“精准扶 贫”精神,某校特制定了一系列关于帮扶A,B两贫困 村的计划,现决定从某地运送152箱鱼苗到A,B两村养 殖,若用大小货车共15辆,则恰好能一次性运完这批鱼 苗.已知这两种大小货车的载货能力分别为12箱/辆和8 箱/辆,其运往A,B两村的运费如下表:
(1)求这15辆车中大小货车各多少辆?(2)现安排其中的10辆货车前往A村,其余货车前往B村, 设前往A村的大货车为x辆,前往A,B两村总费用为y元, 试求出y与x之间的函数解析式.(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你 写出使总费用最少的货车调配方案,并求出最少总费 用.
(1)设大货车有a辆,小货车有b辆,根据题意得 解得 所以这15辆车中大货车有8辆,小货车有7辆.(2)由前往A村的大货车为x辆,知前往B村的大货车 为(8-x)辆,前往A村的小货车为(10-x)辆,前 往B村的小货车为[7-(10-x)]辆,由此可得 y=800x+900(8-x)+400(10-x)+600[7-(10-x)] =100x+9 400(3≤x≤8,且x为整数).
(3)由题意得12x+8(10-x)≥100, 解得x≥5. 因为3≤x≤8且x为整数, 所以5≤x≤8且x为整数. 对于y=100x+9 400,100>0, 所以y随x的增大而增大, 所以当x=5时,y有最小值100×5+9 400=9 900. 所以使总费用最少的货车调配方案是:5辆大货车、 5辆小货车前往A村;3辆大货车、2辆小货车前往B 村,最少总费用为9 900元.
题型2 利润方案2.(2015·济宁)小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题: 服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
(1)设购进甲种服装x件,由题意可知: 80x+60(100-x)≤7 500,解得x≤75. 答:甲种服装最多购进75件.(2)设总利润为w元,则 w=(120-80-a)x+(90-60)(100-x) =(10-a)x+3 000. 因为甲种服装不少于65件,所以65≤x≤75,x为整 数.
方案1:当0
题型1 与方程综合的问题3.(2015·黔西南州)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费.小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;(3)小黄家3月份用水26吨,他家应交水费多少元?
(1)设每吨水的政府补贴优惠价为a元,市场调节价 为b元.根据题意得 解得 答:每吨水的政府补贴优惠价为1元,市场调节 价为2.5元.
(2)当0≤x≤12时,y=x; 当x>12时,y=12+(x-12)×2.5=2.5x-18, 所以所求函数关系式为(3)因为x=26>12, 所以把x=26代入y=2.5x-18, 得y=2.5×26-18=47. 答:他家应交水费47元.
题型2 与不等式综合的问题4.(2016·漳州)某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如下表:(教师按成人票价购买,学生按学生票价购买).
若师生均购买二等座票,则共需1 020元.(1)参加活动的教师有____人,学生有____人.(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票的全部费用为y元. ①求y关于x的函数解析式; ②若购买一、二等座票的全部费用不多于1 032元, 则提早前往的教师最多只能有多少人?
(1)10;50(2)①依题意有 y=26x+22(10-x)+16×50=4x+1 020. 故y关于x的函数解析式是y=4x+1 020. ②依题意有4x+1 020≤1 032, 解得x≤3. 答:提早前往的教师最多只能有3人.
点拨:(1)设参加活动的教师有a人,学生有b人,根据师生人 数和购票费用,列出方程组并求解即可.(2)①根据购买一、二等座票的全部费用=购买一等座 票钱数+教师购买二等座票钱数+学生购买二等座 票钱数,依此可得解析式; ②根据不等关系:购买一、二等座票的全部费用不 多于1 032元,列出不等式求解即可.
建立一次函数模型解实际应用中含图象问题
7.(2015·金华)小慧和小聪沿图①中的景区公路游览.小慧乘坐车速为30 km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑自行车从飞瀑出发前往宾馆,速度为20 km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图②中的图象分别表示两人离宾馆的路程s(km)与时间t(h)之间的函数关系.试结合图中信息回答: (1)小聪上午几点钟从飞瀑出发? (2)试求线段AB,GH的交点B的坐标,并说明它的实际意义. (3)如果小聪到达宾馆后,立即以30 km/h的速度按原路返回, 那么返回途中他几点钟遇见小慧?
(1)小聪骑自行车从飞瀑出发到宾馆所用时间为: 50÷20=2.5(h), 因为上午10:00小聪到达宾馆, 所以小聪上午7点30分从飞瀑出发.
(2)3-2.5=0.5, 所以点G的坐标为(0.5,50), 设直线GH对应的函数解析式为s=kt+b, 把G(0.5,50),H(3,0)的坐标分别代入得 解得 所以s=-20t+60, 当s=30时,t=1.5, 所以点B的坐标为(1.5,30), 点B的实际意义是当小慧出发1.5 h时,小慧与小聪 相遇,且离宾馆的路程为30 km.
初中数学人教版八年级下册19.3 课题学习 选择方案课文配套课件ppt: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c95087_t3/?tag_id=26" target="_blank">19.3 课题学习 选择方案课文配套课件ppt</a>,共22页。PPT课件主要包含了思维导图,课程目标,知识讲解,相关概念,例题讲解,应用练习,课堂小结等内容,欢迎下载使用。
初中数学人教版八年级下册19.3 课题学习 选择方案优秀课件ppt: 这是一份初中数学人教版八年级下册19.3 课题学习 选择方案优秀课件ppt,文件包含193《课题学习选择方案》课件pptx、193《课题学习选择方案》导学案doc、193《课题学习选择方案》教案doc等3份课件配套教学资源,其中PPT共44页, 欢迎下载使用。
人教版八年级下册19.3 课题学习 选择方案优质课课件ppt: 这是一份人教版八年级下册19.3 课题学习 选择方案优质课课件ppt,文件包含193课题学习选择方案pptx、RJ中学数学八年级下第十九章193课题学习选择方案第1课时教学详案docx、RJ中学数学八年级下第十九章193课题学习选择方案第2课时教学详案docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。













