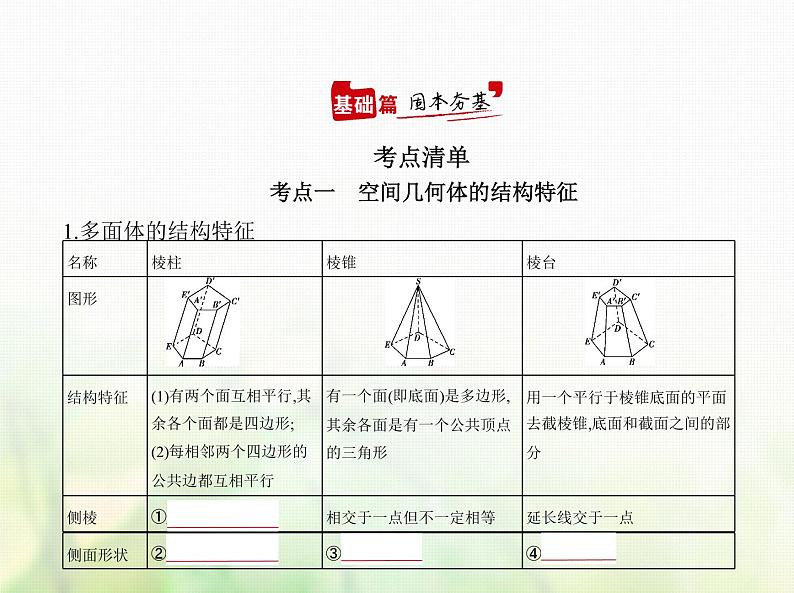
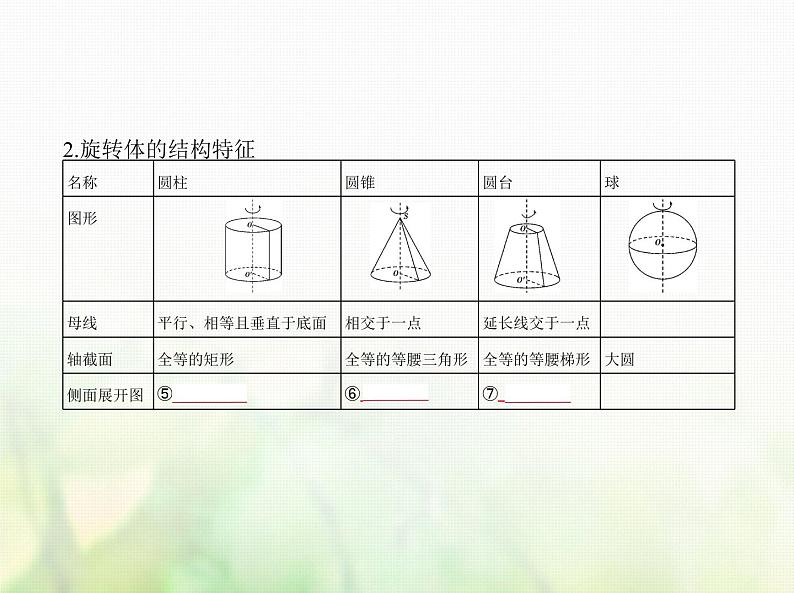


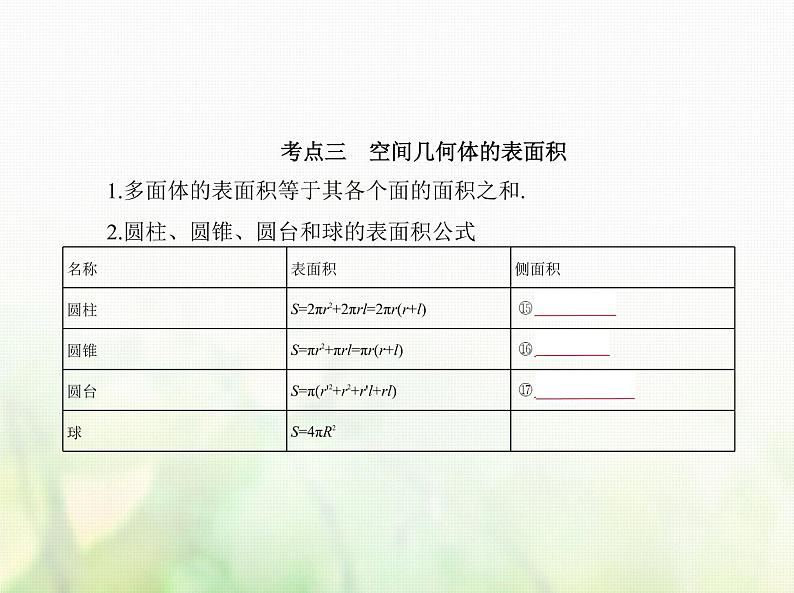



新人教A版高考数学二轮复习专题八立体几何1空间几何体的结构特征表面积与体积综合篇课件
展开3.用斜二测画法画直观图的步骤(1)画几何体的底面在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它 们画成对应的x'轴、y'轴,两轴相交于点O',且使∠x'O'y'=45°(或135°),已知 图形中平行于x轴的线段,在直观图中长度⑧ 保持不变 ,平行于y轴的 线段,长度变为⑨ 原来的一半 .(2)画几何体的高在已知图形中过点O作z轴垂直于平面xOy,在直观图中画出对应的z'轴,垂 直于平面x'O'y',已知图形中平行于z轴的线段,在直观图中平行于z'轴且⑩ 长度不变 .
考点二 空间几何体的体积
考点三 空间几何体的表面积 1.多面体的表面积等于其各个面的面积之和. 2.圆柱、圆锥、圆台和球的表面积公式
考法 与球有关的切、接问题
解题导引 (2)PA=2为定值,点P到平面ABC的距离取最大值时,直线PA与 平面ABC有什么样的位置关系?此时直线PA⊥平面ABC,将三棱锥补成直 三棱柱,利用直三棱柱上、下底面中心的连线的中点是外接球的球心,从 而确定三棱锥P-ABC的外接球球心的位置.
球心O到底面△ABC的距离d= PA=1.在△ABC中,由正弦定理得△ABC的外接圆半径r= = ,所以球O的半径为R= = ,所以球O的表面积为S=4πR2= .
规律总结 1.球的“切”“接”问题的处理规律(1)“切”的处理:球的内切问题主要是球内切于多面体或旋转体.解答时 要找准切点,通过作截面来解决.(2)“接”的处理:把一个多面体的顶点放在球面上即球外接于该多面体. 解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离 等于球的半径.2.与球有关的组合体的常用结论(1)长方体的外接球:①球心:体对角线的交点;②半径:r= (a,b,c为长方体的长、宽、高).
(2)正方体的外接球、内切球及与各条棱都相切的球:①外接球:球心是正方体的中心,半径r= a(a为正方体的棱长);②内切球:球心是正方体的中心,半径r= (a为正方体的棱长);③与各条棱都相切的球:球心是正方体的中心,半径r= a(a为正方体的棱长).(3)正四面体的外接球与内切球(正四面体可以看作正方体的一部分):①外接球:球心是正四面体的中心,半径r= a(a为正四面体的棱长);②内切球:球心是正四面体的中心,半径r= a(a为正四面体的棱长).
例 (2017陕西咸阳二模,14)已知一个三棱锥的所有棱长均为 ,则该三棱锥的内切球的体积为 .
在等边三角形BCD中,BE= × = ,AE= = .由OB2=OE2+BE2,即R2= + ,解得R= ,则OE=AE-R= ,即三棱锥内切球的半径是 ,∴内切球的体积为 π× = π.解法二:因为三棱锥的四个面均为边长是 的等边三角形,所以三棱锥的表面积S=4× × × × =2 .而三棱锥的体积V= × ×( )2× × = .
例 (1)已知四面体P-ABC的四个顶点都在球O的球面上,若PB⊥平面 ABC,AB⊥AC,且AC=1,PB=AB=2,则球O的表面积为 ( )A.7π B.8π C.9π D.10π(2)过球O表面上一点A引三条长度相等的弦AB,AC,AD,且两两夹角都为60°,若球的半径为R,则△BCD的面积为 .(3)在球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB= PC=a,则这个球的表面积为 .
备战2024高考一轮复习数学(理) 第八章 立体几何 第一节 空间几何体的结构特征及表面积与体积课件PPT: 这是一份备战2024高考一轮复习数学(理) 第八章 立体几何 第一节 空间几何体的结构特征及表面积与体积课件PPT,共60页。PPT课件主要包含了多面体的结构特征,任一边,任一直角边,垂直于底边的腰,长对正,高平齐,宽相等,°或135°,平行于坐标轴,长度变为原来的一半等内容,欢迎下载使用。
高考数学二轮复习第2篇3立体几何与空间向量第1讲空间几何体、三视图、表面积与体积课件: 这是一份高考数学二轮复习第2篇3立体几何与空间向量第1讲空间几何体、三视图、表面积与体积课件,共60页。PPT课件主要包含了专题三,高频考点,真题热身,②⑤或③④,感悟高考,考点三多面体与球等内容,欢迎下载使用。
新人教A版高考数学二轮复习专题八立体几何5空间向量及其在立体几何中的应用综合篇课件: 这是一份新人教A版高考数学二轮复习专题八立体几何5空间向量及其在立体几何中的应用综合篇课件,共36页。












