人教B版 (2019)必修 第二册4.5 增长速度的比较课时训练

增长速度的比较　函数的应用(二)

数学建模活动：生长规律的描述

一、选择题

1．向一杯子中匀速注水时，杯中水面高度h随时间t变化的函数h＝f(t)的图像如图所示．则杯子的形状是(　　)

2．当生物死亡后，其体内原有的碳14的含量大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”．当死亡生物体内的碳14含量不足死亡前的千分之一时，用一般的放射性探测器就测不到了．若某死亡生物体内的碳14用该放射性探测器探测不到，则它经过的“半衰期”个数至少是(　　)

A．8　　　B．9

C．10D．11

3．如图所示给出了红豆生长时间t(月)与枝数y(枝)的散点图，那么最能拟合诗句“红豆生南国，春来发几枝”所提到的红豆生长时间与枝数的关系的函数模型是(　　)

A．指数函数：y＝2tB．对数函数：y＝log2t

C．幂函数：y＝t3D．二次函数：y＝2t2

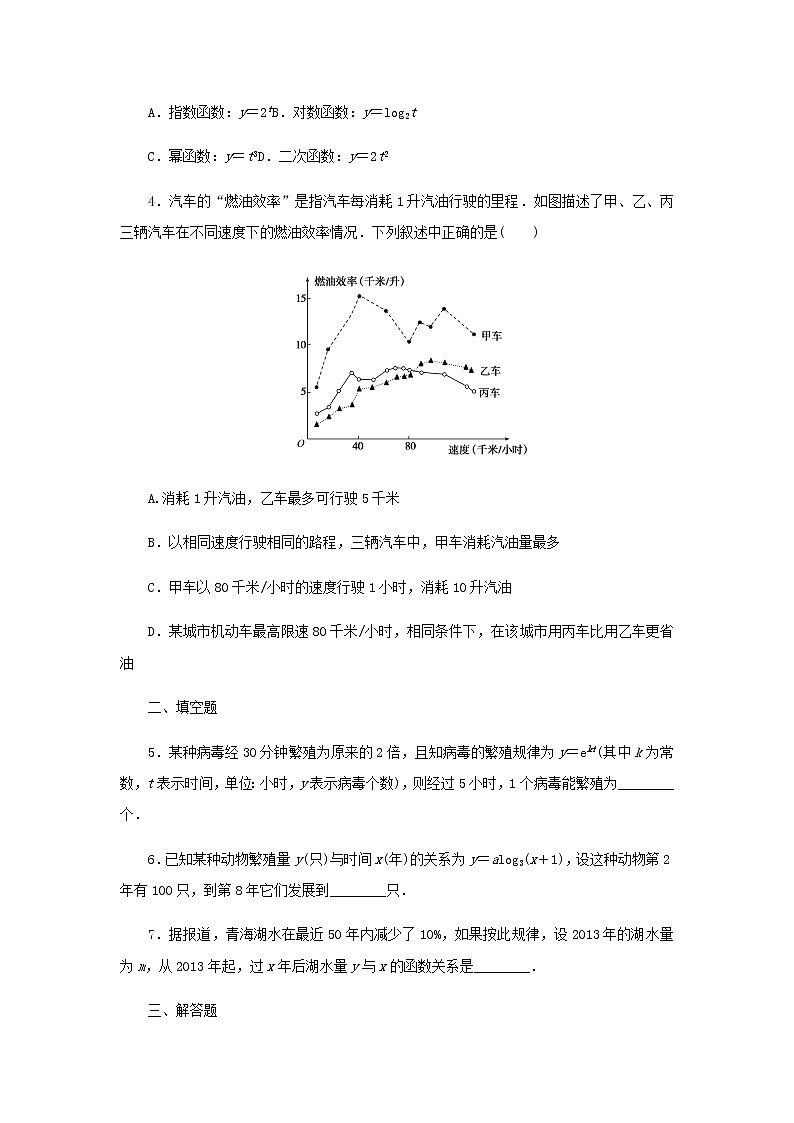
4．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程．如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是(　　)

A.消耗1升汽油，乙车最多可行驶5千米

B．以相同速度行驶相同的路程，三辆汽车中，甲车消耗汽油量最多

C．甲车以80千米/小时的速度行驶1小时，消耗10升汽油

D．某城市机动车最高限速80千米/小时，相同条件下，在该城市用丙车比用乙车更省油

二、填空题

5．某种病毒经30分钟繁殖为原来的2倍，且知病毒的繁殖规律为y＝ekt(其中k为常数，t表示时间，单位：小时，y表示病毒个数)，则经过5小时，1个病毒能繁殖为________个．

6．已知某种动物繁殖量y(只)与时间x(年)的关系为y＝alog3(x＋1)，设这种动物第2年有100只，到第8年它们发展到________只．

7．据报道，青海湖水在最近50年内减少了10%，如果按此规律，设2013年的湖水量为m，从2013年起，过x年后湖水量y与x的函数关系是________．

三、解答题

8．函数f(x)＝lgx，g(x)＝0.3x－1的图像如图所示．

(1)指出曲线C1，C2分别对应哪一个函数；

(2)比较两函数的增长差异(以两图像交点为分界点，对f(x)，g(x)的大小进行比较).

9．某学校开展研究性学习活动，一组同学获得了下面的一组试验数据．

现有如下5个模拟函数：

①y＝0.58x－0.16；②y＝2x－3.02；③y＝x2－5.5x＋8；④y＝log2x；⑤y＝＋1.74.

请从中选择一个模拟函数，使它比较近似地反映这些数据的规律．

[尖子生题库]

10．判断方程2x＝x2有几个实根．

课时作业(十)　增长速度的比较　函数的应用(二)

数学建模活动：生长规律的描述

1．解析：从题图看出，在时间段[0，t1]，[t1，t2]内水面高度是匀速上升的，在[0，t1]上升慢，在[t1，t2]上升快，故选A.

答案：A

2．解析：设该死亡生物体内原有的碳14的含量为1，则经过n个“半衰期”后的含量为，则<，得n≥10，

所以，若某死亡生物体内的碳14用该放射性探测器探测不到，则它至少需要经过10个“半衰期”．

答案：C

3．解析：由散点图可知，与指数函数拟合最贴切，故选A.

答案：A

4．解析：根据图像知消耗1升汽油，乙车最多行驶里程大于5千米，故选项A错；以相同速度行驶时，甲车燃油效率最高，因此以相同速度行驶相同路程时，甲车消耗汽油最少．故选项B错；甲车以80千米/小时的速度行驶时燃油效率为10千米/升，行驶1小时，里程为80千米，消耗8升汽油，故选项C错；最高限速80千米/小时，丙车的燃油效率比乙车高，因此相同条件下，在该市用丙车比用乙车更省油，故选项D对．

答案：D

5．解析：当t＝0.5时，y＝2，所以2＝ek，

所以k＝2ln2，所以y＝e2tln2，

当t＝5时，y＝e10ln2＝210＝1024.

答案：1024

6．解析：y＝alg3(x＋1)

x＝2时y＝100代入得

100＝alg33，∴a＝100

∴当x＝8时y＝100lg39＝200.

答案：200

7．解析：设湖水量每年为上年的q%，

则(q%)50＝0.9，

所以q%＝0.9，所以x年后湖水量y＝m·(q%)x＝m·0.9.

答案：y＝0.9·m(x≥0)

8．解析：(1)由题图知，C1对应的函数为g(x)＝0.3x－1，C2对应的函数为f(x)＝lgx.

(2)当x∈(0，x1)时，g(x)>f(x)；

当x∈(x1，x2)时，g(x)<f(x)；

当x∈(x2，＋∞)时，g(x)>f(x).

9．解析：画出散点图如图所示．

由图可知，上述点大体在函数y＝log2x上(对于y＝0.58x－0.16，可代入已知点验证不符合)，故选择y＝log2x可以比较近似地反映这些数据的规律．

10.

解析：设y1＝x2，y2＝2x，作出这两个函数的图像，由图像知，方程一定有一个负根，当x＞0时，开始y1＝x2在y2＝2x图像的下方，但此时由于y1＝x2比y2＝2x增长的速度快，所以存在x0当x＞x0时，y1＝x2的图像就会在y2＝2x的上方，故此时产生一个实根x0，但最终还是y2＝2x比y1＝x2增长得快，故存在x1，当x＞x1时，y2＝2x的图像又在y1＝x2的上方，故又产生一个实根x1，以后就永远是y2＝2x比y1＝x2增长得快了，故再没有实根了，故此方程有三个实根．