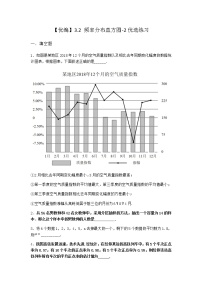
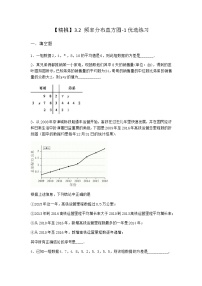
北师大版 (2019)必修 第一册3.1 从频数到频率达标测试

从频数到频率 频率分布直方图

与传统相机比较，在数码相机中，有一种十分实用的功能，这就是直方图显示功能．直方图就是通过在LCD上显示出来的曝光量柱形图来确定照片曝光量大小的工具，通过直方图的横轴和纵轴我们可以直观地看出拍摄的照片的曝光情况，在拍摄时能给摄影者带来很大的方便．

[问题]　你会画这样的柱形图吗？

知识点一　从频数到频率

1．频率表示频数与总数的比值．

2．频率反映了相对总数而言的相对强度，其所携带的总体信息远超过频数．在实际问题中，如果总体容量比较小，频数也可以较客观地反映总体分布；当总体容量较大时，频率就更能客观地反映总体分布．

　容量为100的样本数据被分为6组，如表：

第5组的频率是(　　)

A．0.15　　　　　　　　　 B．0.16

C．0.18  D．0.20

答案：B

知识点二　频率分布直方图

1．定义：频率分布直方图中每个小矩形的底边长是该组的组距，每个小矩形的高是该组的频率与组距的比，从而每个小矩形的面积等于该组的频率，即每个小矩形的面积＝组距×＝频率．我们把这样的图叫作频率分布直方图．

2．频率分布直方图与频率的关系

频率分布直方图以面积的形式反映了数据落在各个小组的频率的大小．

3．频率分布直方图的好处

(1)能清楚直观地显示各组频率分布情况及各组频率之间的差别；

(2)当考虑数据落在若干个组内的频率之和时，可以用相应矩形面积之和来表示．

4．画频率分布直方图的步骤

(1)计算极差；(2)确定组距与组数；(3)分组；(4)列表；(5)画频率分布直方图．

5．频率折线图

在频率分布直方图中，按照分组原则，再在左边和右边各加一个区间，从所加的左边区间的中点开始，用线段依次连接各个矩形的顶端中点，直至右边所加区间的中点，就可以得到一条折线，我们称之为频率折线图．

频率分布直方图应关注的问题

(1)一般地，样本容量越大，所分组数越多，为方便起见，组距的选择力求“取整”，当样本容量不超过120时，按照数据的多少，通常分成5～12组；

(2)画频率分布直方图时，同一组数据，分组时组距要相等，每个矩形的高与频率成正比，这点应特别注意．　　　　

　频数分布直方图与频率分布直方图有什么不同？

提示：频数分布直方图能使我们清楚地知道数据分布在各个小组的个数，而频率分布直方图则是从各小组数据在所有数据中所占的比例大小的角度来表示数据分布的规律．

　对某活动中800名志愿者的年龄抽样调查，统计后得到频率分布直方图(如图)，但是年龄组[25，30)的数据不慎丢失，依据此图回答以下问题：

(1)年龄组[25，30)对应小矩形的高度为________；

(2)据此估计本次活动中志愿者年龄在[25，35)内的人数为________．

解析：(1)设年龄组[25，30)对应小矩形的高度为h，则5×(0.01＋h＋0.07＋0.06＋0.02)＝1，解得h＝0.04.

(2)由(1)得志愿者年龄在[25，35)内的频率为5×(0.04＋0.07)＝0.55，故志愿者年龄在[25，35)内的人数约为0.55×800＝440.

答案：(1)0.04　(2)440

知识点三　其他统计图表

几种表示样本分布的方法的比较

　要反映某市一周内每天的最高气温的变化情况，宜采用(　　)

A．条形统计图  B．扇形统计图

C．折线统计图  D．频率分布直方图

解析：选C　描述数据随时间的变化趋势宜采用折线统计图．

[例1]　已知一个容量是40的样本，把它分成六组，第一组到第四组的频数分别是5，6，7，10，第五组的频率是0.2，那么第六组的频数是________，频率是________．

[解析]　因为频率＝，所以频数＝频率×样本容量，因为第五组的频率是0.2，所以频数是0.2×40＝8，第六组的频数是40－(5＋6＋7＋10＋8)＝4，所以第六组的频率是＝0.1.

[答案]　4　0.1

频数与频率的求解策略

对于频数与频率的问题，首先要明确几个等量关系，即各组的频数之和等于样本容量，各组的频率之和为1，频率＝.在解题过程中，要明确频数、频率以及样本容量之间的关系，弄清已知、未知，选择合适的公式进行解题．　　　　

[跟踪训练]

一个容量为20的样本数据，分组后组距与频数如下表：

则样本数据在区间[10，50)上的频率为________．

解析：区间[10，50)包括四部分的数据，在这四部分上的数据的频数和是2＋3＋4＋5＝14，样本容量为20，所以样本数据在区间[10，50)上的频率为＝0.7.

答案：0.7

[例2]　(链接教科书第161页例3)为了了解某片经济林的生长情况，随机测量其中的100棵树的底部周长，得到如下数据(单位：cm)：

(1)列出频率分布表；

(2)画出频率分布直方图及频率折线图；

(3)估计该片经济林中底部周长小于100 cm的树占多少，底部周长不小于120 cm的树占多少．

[解]　(1)这组数据的最大的数为135，最小的数为80，最大的数与最小的数的差为55，可将该组数据分为11组，组距为5.

频率分布表如下：

(2)频率分布直方图和频率折线图如图所示．

(3)从频率分布表得，样本中底部周长小于100 cm的频率为0.01＋0.02＋0.04＋0.14＝0.21，样本中底部周长不小于120 cm的频率为0.11＋0.06＋0.02＝0.19.所以估计该片经济林中底部周长小于100 cm的树占21%，底部周长不小于120 cm的树占19%.

绘制频率分布直方图应注意的2个问题

(1)在绘制出频率分布表后，画频率分布直方图的关键就是确定小矩形的高．一般地，频率分布直方图中两坐标轴上的单位长度是不一致的，合理的定高方法是“以一个恰当的单位长度”(没有统一规定)，然后以各组的“频率/组距”所占的比例来定高．如我们预先设定以“”为一个单位长度，代表“0.1”，则若一个组的为0.2，则该小矩形的高就是“”(占两个单位长度)，如此类推；

(2)数据要合理分组，组距要选取恰当，一般尽量取整，数据为30～120个左右时，应分成5～12组，在频率分布直方图中，各个小长方形的面积等于各组的频率，小长方形的高与频数成正比，各组频数之和等于样本容量，频率之和为1.　　　　

[跟踪训练]

　有一容量为50的样本，数据的分组及各组的频数如下：

[10，15)，4；[15，20)，5；[20，25)，10；[25，30)，11；[30，35)，9；[35，40)，8；[40，45]，3.

(1)求出样本中各组的频率；

(2)画出频率分布直方图及频率折线图．

解：(1)由所给的数据，可得下表：

(2)频率分布直方图如图①所示，频率折线图如图②所示．

[例3]　(链接教科书第163页思考交流)为了了解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图所示)，图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3，第二小组频数为12.

(1)第二小组的频率是多少？样本容量是多少？

(2)若次数在110以上(含110次)为达标，试估计该校全体高一学生的达标率是多少？

[解]　(1)由于频率分布直方图以面积的形式反映了数据落在各个小组内的频率大小，因此第二小组的频率为＝0.08.

又因为第二小组频率＝，

所以样本容量＝＝＝150.

(2)由题图可估计该校高一学生的达标率约为

×100%＝88%.

[母题探究]

1．(变设问)若本例条件不变，试求样本中不达标的学生人数．

解：由达标率为88%，样本容量为150，不达标的学生频率为1－0.88＝0.12.所以样本中不达标的学生人数为150×0.12＝18.

2．(变设问)若本例条件不变，试求第三小组的频数．

解：第三小组的频率为＝0.34.

又因为样本容量为150.

所以第三小组的频数为150×0.34＝51.

由频率分布直方图进行相关计算时，需掌握下列关系式：

(1)×组距＝频率；

(2)＝频率，此关系式的变形为：＝样本容量，样本容量×频率＝频数．　　　　

[跟踪训练]

　某电子商务公司对10 000名网络购物者2020年度的消费情况进行统计，发现消费金额(单位：万元)都在区间[0.3，0.9]内，其频率分布直方图如图所示．

(1)直方图中的a＝________；

(2)在这些购物者中，消费金额在区间[0.5，0.9]内的购物者的人数为________．

解析：(1)由0.1×1.5＋0.1×2.5＋0.1a＋0.1×2.0＋0.1×0.8＋0.1×0.2＝1，解得a＝3.

(2)区间[0.3，0.5)内的频率为0.1×1.5＋0.1×2.5＝0.4，故[0.5，0.9]内的频率为1－0.4＝0.6.

因此，消费金额在区间[0.5，0.9]内的购物者的人数为0.6×10 000＝6 000.

答案：(1)3　(2)6 000

[例4]　如图是根据某市3月1日至3月10日的最低气温(单位：℃)的情况绘制的折线统计图，试根据折线统计图反映的信息，绘制该市3月1日到10日最低气温(单位：℃)的扇形统计图和条形统计图．

[解]　该城市3月1日至10日的最低气温(单位：℃)情况如下表：

其中最低气温为－3 ℃的有1天，占10%；最低气温为－2 ℃的有1天，占10%；最低气温为－1 ℃的有2天，占20%；最低气温为0 ℃的有2天，占20%；最低气温为1 ℃的有1天，占10%；最低气温为2 ℃的有3天，占30%，扇形统计图和条形统计图如图所示．

1．条形图是用一个单位长度表示一定的数量或频率，根据数量的多少或频率的大小画成长短不同的矩形条，条形图能清楚地表示出每个项目的具体数目或频率．

2．扇形图是用整个圆面积表示总数(100%)，用圆内的扇形面积表示各个部分所占总数的百分数．

3．在画折线图时，要注意明确横轴、纵轴的实际含义．　　　　

[跟踪训练]

1．如图是根据某中学为地震灾区捐款的情况而制作的统计图．已知该校在校学生3 000人，根据统计图计算该校共捐款________元．

解析：根据统计图，得

高一人数为3 000×32%＝960，捐款960×15＝14 400(元)；

高二人数为3 000×33%＝990，捐款990×13＝12 870(元)；

高三人数为3 000×35%＝1 050，捐款1 050×10＝10 500(元)．

所以该校学生共捐款14 400＋12 870＋10 500＝37 770(元)．

答案：37 770

2．甲、乙两个城市2021年4月中旬，每天的最高气温统计图如图所示，这9天里，气温比较稳定的城市是________．

解析：从折线统计图中可以很清楚的看到乙城市的气温变化较大，而甲城市气温相对来说较稳定，变化基本不大．

答案：甲

1．从一堆苹果中任取了20个，并得到它们的质量(单位：克)数据分布表如下：

根据频数分布表，可以估计在这堆苹果中，质量大于130克的苹果数约占苹果总数的(　　)

A．10%　　　　　　　　 B．30%

C．60%  D．80%

解析：选C　根据频数分布表可知，＝＝＝0.6，所以质量大于130克的苹果数约占苹果总数的60%.故选C.

2．有一个容量为200的样本，样本数据分组为[50，70)，[70，90)，[90，110)，[110，130)，[130，150]，其频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在区间[90，110)内的频数为(　　)

A．48  B．60

C．64  D．72

解析：选B　由(0.005 0＋0.007 5＋0.010 0＋0.012 5＋a)×20＝1，解得a＝0.015，所以样本数据落在区间[90，110)内的频率为0.015×20＝0.3，所以样本数据落在区间[90，110)内的频数为200×0.3＝60，故选B.

3．某班全体学生英语测试成绩(单位：分)的频率分布直方图如图所示，数据的分组依次为[20，40)，[40，60)，[60，80)，[80，100]．若低于60分的人数是15，则该班的学生人数是(　　)

A．45  B．50

C．55  D．60

解析：选B　根据频率分布直方图，可知低于60分的人数的频率是(0.005＋0.010)×20＝0.3，所以该班的学生人数是＝50.

4．(多选)如图给出的是某高校土木工程系大四55名学生期末考试专业成绩的频率折线图，其中组距为10，且本次考试中最低分为50分，最高分为100分．根据图中所提供的信息，下列结论中正确的是(　　)

A．成绩是75分的人数为20

B．成绩是100分的人数比成绩是50分的人数多

C．成绩落在[70，90)内的人数为35

D．成绩落在[70，80)内的人数为20

解析：选CD　成绩落在[70，80)内的人数为10××55＝20，不能说成绩是75分的人数为20，所以A错误，D正确；从频率折线图看不出成绩是100分的人数比成绩是50分的人数多，只能看出成绩落在[50，60)内的人数和成绩落在[90，100]内的人数相等，所以B错误；成绩落在[70，90)内的人数为×55＝35，所以C正确．

5．交通管理部门为了解某一段公路上小汽车的行驶速度，随机抽取了200辆通过这一段公路的小汽车，其速度的频率分布直方图如图所示，则这200辆汽车中在该路段上行驶速度低于60 km/h的有________辆．

解析：由频率分布直方图，可知该路段上行驶速度低于60 km/h的有200×(0.01＋0.03)×10＝80(辆)．

答案：80