2022年山东省菏泽市巨野县中考一模数学试题(word版含答案)

这是一份2022年山东省菏泽市巨野县中考一模数学试题(word版含答案)，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
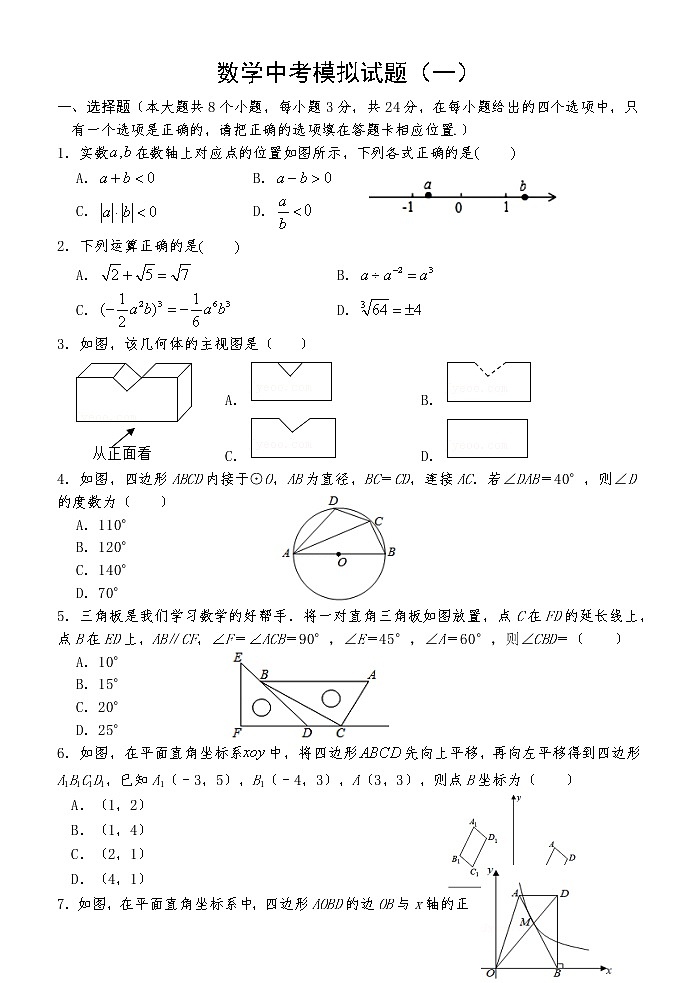
数学中考模拟试题（一）一、选择题（本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中，只有一个选项是正确的，请把正确的选项填在答题卡相应位置.）1．实数在数轴上对应点的位置如图所示，下列各式正确的是　　A．    B． C．        D．2．下列运算正确的是　　A．      B．C．    D．3．如图，该几何体的主视图是（　　）A．    B． C．   D．4．如图，四边形ABCD内接于⊙O，AB为直径，BC＝CD，连接AC．若∠DAB＝40°，则∠D的度数为（　　）A．110°  B．120°   C．140°  D．70°5．三角板是我们学习数学的好帮手．将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，则∠CBD＝（　　）A．10° B．15° C．20° D．25°6．如图，在平面直角坐标系中，将四边形先向上平移，再向左平移得到四边形A1B1C1D1，已知A1（﹣3，5），B1（﹣4，3），A（3，3），则点B坐标为（　　）A．（1，2） B．（1，4） C．（2，1） D．（4，1）7．如图，在平面直角坐标系中，四边形AOBD的边OB与x轴的正半轴重合，AD∥OB，DB⊥x轴，对角线AB，OD交于点M．已知AD：OB＝2：3，△AMD的面积为4．若反比例函数y＝的图象恰好经过点M，则k的值为（　　）A．   B．12    C．    D.8．如图1，在△ABC中，∠A＝∠B＝45°，E，F分别是边AC，BC上的动点，且AE＝CF，D是AB的中点，连接DE，DF，EF，设BF＝x，△CEF的面积为y，图2是y关于x的函数图象，则下列说法不正确的是（　　）A．△DEF是等腰直角三角形B．m＝1C．四边形CEDF的面积为2              D．△CEF的周长可以等于6二、填空题（本大题共6个小题，每小题3分，共18分，请把最后结果填写在答题卡的相应区域内）9．分解因式　        　10．2021年5月，由中国航天科技集团研制的天问一号探测器的着陆巡视器成功着陆于火星乌托邦平原南部预选着陆区．中国航天器首次奔赴火星，就“毫发未损”地顺利出现在遥远的红色星球上，完成了人类航天史上的一次壮举．火星与地球的最近距离约为5500万千米，该数据用科学记数法可表示为　 　  千米．11．关于的一元二次方程有实数根，则的取值范围是　    　．12．在菱形中，,其周长为24，则菱形的面积为　　      ．13.已知一组从小到大排列的数据：2，5，，11的平均数与中位数都是7，则这组数据的众数是　　      ．14．如图，已知直线，过点作轴的垂线交直线于点，过点作直线的垂线交轴于点；过点作轴的垂线交直线于点，过点作直线的垂线交轴于点；…；按此作法继续下去，则点的坐标为　    　．三、解答题（本大题共10个小题，共78分，请把解答或证明过程写在答题卡的相应区域内）15.（6分）计算：．16.（6分）先化简再求值：，其中a是不等式组的最小整数解.17.（6分）已知：如图，点A、B、C、D在一条直线上，EA∥FB，EA＝FB，AB＝CD.（1）求证：∠E＝∠F；（2）若∠A＝400，∠D＝800，求∠E的度数．18.(6分)巨野永丰塔始建于后周，北宋年间建成，是第七批国家重点文物保护单位，作为巨野县标志性建筑，现已成为我市游客到巨野游玩的网红地．如图，为测量永丰塔的高度，某数学兴趣小组在永丰塔附近一建筑物楼顶D处测得塔A处的仰角为45°，塔底部B处的俯角为22°．已知建筑物的高CD约为8.8米，请计算观景台的高AB的值．（参考数据：，，）19．（7分）如图，反比例函数y＝的图象与一次函数y＝kx+b的图象交于A、B两点，点A的坐标为（2，6），点B的坐标为（n，1）．(1)求n的值，一次函数解析式；(2)结合图象，直接写出不等式＜kx+b的解集． 20．（7分）某地响应“把绿水青山变成金山银山，用绿色杠杆撬动经济转型”发展理念，开展“美化绿色城市”活动，绿化升级改造了总面积为360万平方米的区域．实际施工中，由于采用了新技术，实际平均每年绿化升级改造的面积是原计划平均每年绿化升级改造的面积的2倍，所以比原计划提前4年完成了上述绿化升级改造任务．实际平均每年绿化升级改造的面积是多少万平方米？21．（10分）．如图，已知点E在△ABC的边AB上，的平分线交BC于点D，且D在以AE为直径的⊙O上．（1）求证：BC是⊙O的切线；（2）若DC＝4，AC＝6，，求圆心O到AD的距离． 22.（10分）为响应“学雷锋、树新风、做文明中学生”的号召，某校开展了志愿者服务活动，活动项目有“防疫宜宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查，结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如下不完整的条形统计图和扇形统计图．根据以上统计图解答下列问题：（1）本次随机抽取的学生共有______名；（2）补全条形统计图；（3）若该校有3000名学生，请估计参与了4项活动的学生人数；（4）在这次活动中小亮和小颖同学都只选择了一项活动，请你利用表格或树状图求小亮和小颖选择同一项活动的概率．23.（10分）在正方形ABCD中，点E为边AB上的点，连结DE，过点A作AG⊥DE交BC于点G，垂足为点F．（1）如图1，AE与BG相等吗？请说明理由；（2）如图2，连接BD，交AG于点H，连接EH，若BE:AE＝n，求DH:BH；（3）在（2）的基础上，如图3，当EH∥AD时，求n的值．24.（10分）如图，抛物线与x轴交于A(－1，0)、B(3，0)，交y轴于C(0，3)．（1）求抛物线的解析式；（2）P是直线BC上方的抛物线上的一个动点，设P的横坐标为t，P到BC的距离为h，求h与t的函数关系式，并求出h的最大值；（3）设点M是x轴上的动点，在平面直角坐标系中，存在点N，使得以点A、C、M、N为顶点的四边形是菱形，直接写出所有符合条件的点N坐标．  数学中考模拟一参考答案1、D 2、B 3、C 4、A 5、B 6、C 7、A 8、D   cm 2        15.。。。。。。。。。6分16．。。。。。。。。。。。。。。。。。。。。。3分 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分原式=。。。。。。。。。。。。。。。。。。。。。。。。。6分17（1）∠E=∠F；.。。。。。。。。。。。。。。。。。。。。。。。。。。3分（2）∠E=180°-∠A-∠ACE=60°.。。。。。。。。。。。。。。。。。。。。6分18.DM=22米。。。。。。。。。。。。。。。。。。。。。。。。2分观景台的高约为30.8米．。。。。。。。。。。。。。。。。。6分19．(1)n＝12。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分直线AB解析式为y＝﹣x+7。。。。。。。。。。。。。。。。。。。。。4分(2)根据函数图象可得满足题意的x的范围是：2＜x＜12或x＜0。。。。。。。。。 7分20．解：设原计划每年绿化升级改造的面积是x万平方米，则实际每年绿化升级改造的面积是2x万平方米，根据题意，得：，。。。。。。。。。。。。。。。。。。。。。。。。。。。。。3分解得：x=45，.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分经检验，x=45是原分式方程的解，符合题意则2x=2×45=90．答：实际平均每年绿化升级改造的面积是90万平方米．。。。。。。。。。。。。7分21．（1）。。。。。。。。。。。。。。。。。。。。。。5分（2）圆心到的距离是：．。。。。。。。。。。。。。10分22.解：（1）50名.。。。。。。。。。。。。。。。。。。。。。。1分 （2）活动数为5项的人数为6名。。。。。。2分补全条形统计图如解图。。。。。。。。。。。。。。。。。。。。3分（3）估计参与了4项活动的学生大约有720人；。。。。。。。。。。。。。。。6分（4）树状图或概率（略）。。。。。。。。。。。。。。。。10分23.(1)解：。。。。。。。。。。。。。。。。。。。。。。1分理由。。。。。。。。。。。。。。。。。。。。。。。。。。。4分(2)，，；。。。。。。。。。。。。。。。。。。。。。7分(3)设，则，，，，，，，，，，，，，，．。。。。。。。。。。。。。。。。。。。。。。。。。10分24．解：（1）抛物线的解析式为y=-x2+2x+3；。。。。。。。。。。。。。2分（2）过点P作PD⊥x轴于点D，交BC于点E，PH⊥BC于点H，连接PB、PC．∵B（3，0）、C（0，3），∴OB=OC=3，BC=，设直线BC解析式为y=kx+n，则，解得 ，∴直线BC解析式为y=-x+3，∵点P的横坐标为t，且在抛物线y=-x2+2x+3上，∴P（t，-t2+2t+3），又∵PD⊥x轴于点D，交BC于点E，∴D（t，0），E（t，-t+3），∴PE=(-t2+2t+3)-(-t+3)=-t2+3t，∴S△PBC=PE•()=(−t2+3t)×3=−t2+t，又∵S△PBC=BC•PH=×3•h=h，∴h=−t2+t，∴h与t的函数关系式为：h=−t2+t（0＜t＜3），∵，∴当t=时，h有最大值为；。。。。。。。。。。。。。。。。。。。。6分（3）存在．若AM为菱形对角线，则AM与CN互相垂直平分，∴N（0，-3）；若CM为菱形对角线， 则CN=AM=AC=，∴N(−，3)或N(，3)；若AC为菱形对角线，则CN=AM=CM，设M（m，0），由CM2=AM2，得m2+32=(m+1)2，解得m=4，∴CN=AM=CM=5，∴N（-5，3）．综上可知存在点N，使得以点A、C、M、N为顶点的四边形是菱形，符合条件的点N有4个：（0，-3），(−，3)，(，3)，（-5，3）．。。。。。。。。。。。。。。10分