高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直教课ppt课件

这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直教课ppt课件，共22页。PPT课件主要包含了必备知识生成，°θ≤90°，a⊥b，关键能力探究，核心知识，易错提醒，核心素养，方法总结，直线与直线垂直，异面直线所成的角等内容，欢迎下载使用。
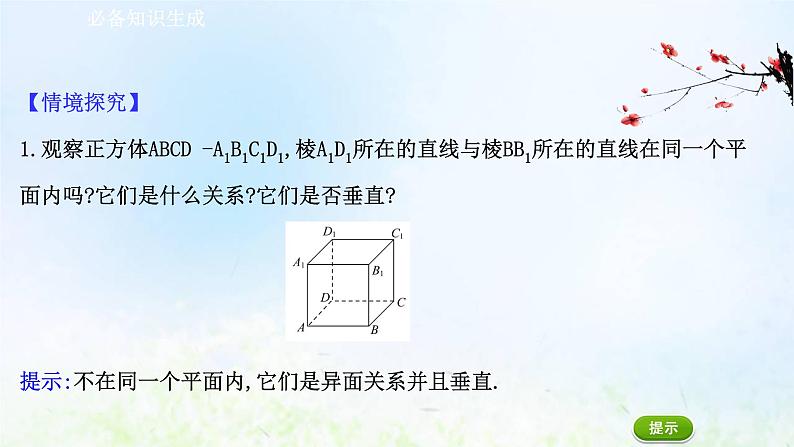
【情境探究】1.观察正方体ABCD -A1B1C1D1,棱A1D1所在的直线与棱BB1所在的直线在同一个平面内吗?它们是什么关系?它们是否垂直?提示:不在同一个平面内,它们是异面关系并且垂直.
2.如何判断空间两直线垂直?提示:通过平移把异面直线转化为相交直线,若两条相交直线所成的角是90°,则两直线垂直.
【知识生成】两异面直线所成的角及空间两条直线垂直
探究点一　求异面直线所成的角【典例1】在空间四边形ABCD中,AB=CD,AB与CD成30°角,E,F分别为BC,AD的中点,求EF与AB所成的角.【思维导引】取BD的中点G,连接EG,FG,因为E,F分别为BC,AD的中点,根据三角形中位线定理可得,∠GFE就是EF与AB所成的角,AB与CD所成角为30°,所以∠EGF=30°或150°,利用等腰三角形的性质可得结果.
【解析】取BD的中点G,连接EG,FG,因为E,F分别为BC,AD的中点,所以EG∥CD且EG= CD,GF∥AB且GF= AB. 所以EG与GF所成的角即为AB与CD所成的角或它的补角,因为AB=CD,所以△EFG为等腰三角形.又AB与CD所成角为30°,所以∠EGF=30°或150°,因为∠GFE就是EF与AB所成的角,所以EF与AB所成角为75°或15°.
【类题通法】求两条异面直线所成的角的一般步骤及口诀　(1)一般步骤①构造:根据异面直线的定义,用平移法(常用三角形的中位线、平行四边形的性质)作出异面直线所成的角.②证明:证明作出的角就是要求的角.③计算:求角度,常利用三角形.④结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
(2)口诀中点、端点定顶点,平移常用中位线;平行四边形中见,指出成角很关键;求角构造三角形,锐角、钝角要明辨;平行线若在外,补上原体在外边.
【定向训练】　如图所示,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,求异面直线DE与AB所成的角.
【解析】因为D,E分别是VB,VC的中点,所以BC∥DE,因此∠ABC是异面直线DE与AB所成的角,又因为AB是圆O的直径,点C是弧AB的中点,所以△ABC是以∠ACB为直角的等腰直角三角形,于是∠ABC=45°,故异面直线DE与AB所成的角为45°.
探究点二　空间两直线垂直【典例2】如图,在空间四边形ABCD中,两条对边AB=CD=3,E,F分别是另外两条对边AD,BC上的点,且 EF= .求证:AB⊥CD.【思维导引】转化为利用直线垂直判定定理求解.
【证明】如图,过E作EO∥AB,交BD于点O,连接OF,所以 所以OF∥CD,所以∠EOF(或其补角)是AB和CD所成的角.在△EOF中,OE= AB=2,OF= CD=1.又EF= ,所以EF2=OE2+OF2,所以∠EOF=90°.所以AB⊥CD.
【类题通法】证明两异面直线垂直的步骤　(1)作出两异面直线所成的角.(2)求出两异面直线所成角的余弦值或在特殊三角形中说明垂直关系.(3)结论.
【定向训练】已知正方体ABCD -A1B1C1D1的棱长为1,O是底面ABCD的中心,求证OD1⊥A1C1.
【证明】连接AC,BD,交点为O,连接AD1,因为A1C1∥AC,所以∠AOD1是异面直线OD1与A1C1所成的角(或所成角的补角),因为OA= AD1= 所以cs∠AOD1= 所以∠AOD1=90°.所以异面直线OD1与A1C1所成的角为90°.所以OD1⊥A1C1.
直观想象：求作异面直线所成角的问题
异面直线所成的角的求法(1)作：利用中位线、长方体、平行四边形等性质平移至一个三角形，并说明为异面直线所成的角或补角. (2)求：利用余弦定理求角（如果是特殊三角形），或利用三角形的性质求角。
求异面直线所成的角时注意的范围
1.若空间两条直线a和b没有公共点,则a与b的位置关系是(　　)　　　　　　　　　　　　　　　　　A.共面B.平行C.异面D.平行或异面【解析】选D.若直线a和b共面,则由题意可知a∥b;若a和b不共面,则由题意可知a与b是异面直线.
2.如图所示,在正方体ABCD -A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小为(　　) A.30°B.45°C.60°D.90°【解析】选C.连接B1D1,D1C,则B1D1∥EF,故∠D1B1C为所求,又B1D1=B1C=D1C,所以∠D1B1C=60°.
3.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,AA1= AB.记异面直线AB1与BD所成的角为θ,则cs θ的值为________. 
【解析】连接B1D1,AD1,因为在直四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形, 所以BD∥B1D1,所以∠AB1D1是异面直线AB1与BD所成的角(或所成的角的补角),设AA1= AB= ,所以AD1=AB1= =2,B1D1= ,记异面直线AB1与BD所成的角为θ,则cs θ= 答案: