高中数学人教A版 (2019)必修 第二册8.1 基本立体图形集体备课ppt课件

这是一份高中数学人教A版 (2019)必修 第二册8.1 基本立体图形集体备课ppt课件，共39页。PPT课件主要包含了必备知识生成，O′O，直角边，OO′，或挖去，关键能力探究，课堂素养达标等内容，欢迎下载使用。
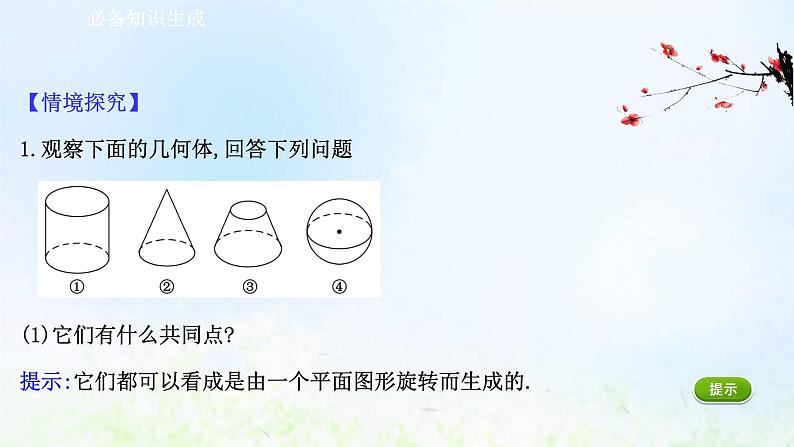
【情境探究】1.观察下面的几何体,回答下列问题 (1)它们有什么共同点?提示:它们都可以看成是由一个平面图形旋转而生成的.
(2)它们分别由什么样的平面图形旋转而成的?提示:①是由矩形绕其中一边所在直线旋转而成.②是由直角三角形绕其中一直角边所在直线旋转而成.③是由直角梯形绕垂直于底边的腰所在直线旋转而成.④是由半圆绕直径所在直线旋转而成.
2.观察下面的几何体,回答有关问题: (1)组合体①、②是由哪些简单几何体组合成的?提示:①是由一个三棱柱挖出一个圆柱组合而成的.②是由一个圆台和两个圆柱组合而成的.
(2)通过观察你发现组合体①与组合体②的组合有何不同?提示:组合体①是由简单几何体挖出一个简单几何体组成的.组合体②是由几个简单几何体拼接而成的.
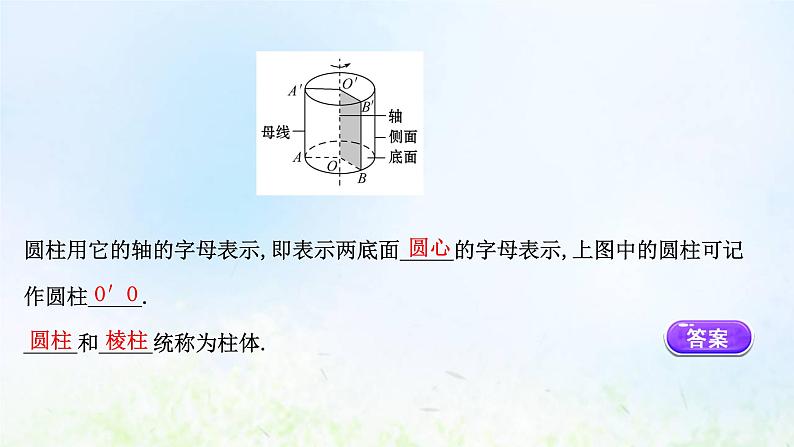
【知识生成】1.圆柱的结构特征以_____的一边所在直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的___;垂直于轴的边旋转而成的圆面叫做圆柱的_____;平行于轴的边旋转而成的曲面叫做圆柱的_____;无论旋转到什么位置,_____于轴的边都叫做圆柱侧面的_____.
圆柱用它的轴的字母表示,即表示两底面_____的字母表示,上图中的圆柱可记作圆柱_____._____和_____统称为柱体.
2.圆锥的结构特征以_____三角形的一条_______所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体叫做圆锥.圆锥用它的轴___表示,底面为____,SA为母线.另外,S叫做圆锥的_____,OA(或OB)叫做底面☉O的_____._____与_____统称为锥体.
3.圆台的结构特征用平行于_____底面的平面去截圆锥,_____与_____之间的部分叫做圆台.
圆锥的底面和截面分别叫做圆台的___底面和___底面.与圆柱和圆锥一样,圆台也有轴、_____、母线,如图所示,轴为_____,AA′为母线.圆台用它的轴的_____表示,如图中的圆台可记作圆台_____._____与_____统称为台体.
4.球半圆以它的_____所在直线为旋转轴,旋转_____形成的曲面叫做_____,球面所围成的旋转体叫做球体,简称球.半圆的_____叫做球的球心;连接_____和球面上任意一点的线段叫做球的半径;连接球面上两点并且经过球心的线段叫做球的直径.球常用表示_____的字母表示,如图中的球记作球__.
5.简单组合体(1)概念:_____________________________.(2)两种基本形式:一种是由简单几何体_____而成,一种是由简单几何体____________一部分而成.
由简单几何体组合而成的几何体
探究点一　旋转体的结构特征【典例1】下列叙述正确的是________. ①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②以等腰三角形的底边上的高所在的直线为旋转轴,其余各边旋转一周形成的曲面围成的几何体是圆锥;③球的半径是球面上任意一点和球心的连线段的长度;④球面上任意三点可能在一条直线上;⑤用一个平面去截球,得到的截面是一个圆面.【思维导引】理解旋转体的定义,利用各旋转体的性质,作出判断.
【解析】①以直角三角形的一条直角边为轴旋转一周才可以得到圆锥;②正确;根据球的半径定义可知③正确;球面上任意三点一定不共线,故④错误;用一个平面去截球,一定截得一个圆面,故⑤正确.答案:②③⑤
【类题通法】判断旋转体形状的关键(1)判断旋转体类型的关键是轴的确定,看旋转体是由平面图形绕哪条直线旋转所得,同一个平面图形绕不同的轴旋转,所得的旋转体一般是不同的.(2)处理旋转体识图问题时,要抓住圆柱和圆锥定义中的关键点:①矩形或直角三角形绕轴旋转形成,其特征是轴所在直线必须与底面垂直;②矩形或直角三角形旋转到任何位置时其形状不能发生变化.
【定向训练】1.下列关于圆柱的说法中不正确的是(　　)A.圆柱的所有母线长都相等B.用平行于圆柱底面的平面截圆柱,截面是与底面全等的圆面C.用一个不平行于圆柱底面的平面截圆柱,截面是一个圆面D.一个矩形以其对边中点的连线为旋转轴,旋转180°所形成的几何体是圆柱【解析】选C.根据圆柱的定义和结构特征,易知C不正确.
2.一个有30°角的直角三角板绕其各条边所在直线旋转所得的几何体是圆锥吗?如果以斜边上的高所在的直线为轴旋转180°得到什么图形?【解析】如图①②旋转一周围成的几何体是圆锥,如图③旋转一周所得的几何体是两个圆锥的组合体;如图④旋转180°是两个半圆锥的组合体.
探究点二　简单组合体的结构特征【典例2】如图,观察下列几何体,分析它们是由哪些简单几何体组成的,并说出主要结构特点.
【思维导引】观察组合体的结构特征,主要弄清它是由哪些简单几何体组成的,必要时可指出棱数、面数和顶点数.
【解析】题干图中,图(1)是由一个四棱柱在它的上、下底面上向内挖去一个三棱柱组成的几何体,它有9个面,14个顶点,21条棱,具有四棱柱和三棱柱的结构特征.图(2)是由一个四棱柱和一个底面与四棱柱上底面重合的四棱锥组成的几何体,有9个面,9个顶点,16条棱,具有四棱柱和四棱锥的结构特征.图(3)是由一个三棱柱和一个底面与三棱柱的上底面重合的三棱台组成的几何体,有9个顶点,8个面,15条棱,具有三棱柱和三棱台的结构特征.
【类题通法】判断组合体构成的方法技巧(1)首先要熟练掌握简单几何体的结构特征;其次要善于将复杂的组合体“分割”为几个简单的几何体.(2)要仔细观察组合体的构成,结合柱、锥、台、球的结构特征,先分割,后验证.
【定向训练】1.已知AB是直角梯形ABCD中与底边垂直的一腰,如图.分别以AB,BC,CD,DA所在直线为轴旋转,试说明所得几何体的结构特征.
【解析】(1)以AB所在直线为轴旋转所得旋转体是圆台.如图①所示.(2)以BC边所在直线为轴旋转所得的旋转体是一组合体:下部为圆柱,上部为圆锥.如图②所示.
(3)以CD边所在直线为轴旋转所得的旋转体为一组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥.如图③所示.(4)以AD边所在直线为轴旋转所得的旋转体为一组合体:一个圆柱上部挖去一个圆锥.如图④所示.
2.如图,AB为圆弧BC所在圆的直径,∠BAC=45°.将这个平面图形绕直线AB旋转一周,得到一个组合体,试说明这个组合体的结构特征.
【解析】如图所示,这个组合体是由一个圆锥和一个半球体拼接而成的.
探究点三　旋转体的截面问题【典例3】如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,求圆台O′O的母线长.
【思维导引】旋转体的轴截面中有母线、底面半径、高等主要元素,因而,在涉及这些元素的计算时,通常利用轴截面求解.在圆台的轴截面中,将等腰梯形的两腰延长,在三角形中可借助相似求解.
【解析】设圆台的母线长为l cm,由截得圆台上、下底面面积之比为1∶16,可设截得圆台的上、下底面的半径分别为r、4r.过轴SO作截面,如图所示. 则△SO′A′∽△SOA,SA′=3 cm.所以 所以 解得l=9,即圆台的母线长为9 cm.
【类题通法】旋转体的轴截面及应用用平行于底面的平面去截柱、锥、台等几何体,注意抓住截面的性质(与底面全等或相似),同时结合旋转体中的经过旋转轴的截面(轴截面)的性质,利用相似三角形的性质,设相关几何量的方程组求解.
【定向训练】1.如图中的几何体是由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体,则所截得的图形可能是图中的(　　) 　　　　　　　　　　　　　　　　　　　A.(1)(2)B.(1)(3)C.(1)(4)D.(1)(5)
【解析】选D.组合体的上底面已经挖去,故(2)(3)必错;当截面不过轴时,与圆锥的截线不可能是直线,故(4)错.
2.一圆锥的母线长为6,底面半径为3,把该圆锥截一圆台,截得圆台的母线长为4,则圆台的另一底面半径为________. 【解析】作轴截面如图, 则 所以r=1.答案:1
求圆柱、圆锥、圆台侧面上两点间最短距离都要转化到侧面展开图中，“化曲为直”是求几何体表面上两点间最短距离的好方法．
1.判断简单旋转体结构特征的方法
1.数学抽象：圆柱、圆锥、圆台、球的定义．；2.逻辑推理：圆柱、圆锥、圆台、球的结构特征．；3.数学运算：旋转体的母线、底面圆半径、球的相关计算4.直观想象：简单组合体的结构特征。
1.明确由哪个平面图形旋转而成． 2.明确旋转轴是哪条直线．
2.旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构 特征的关键量．
1.圆柱： 定义，相关概念 2.圆锥： 定义，相关概念3.圆台： 定义，相关概念4.球： 定义，相关概念5.组合体: 定义
1.下列叙述中正确的个数是(　　)①圆柱的母线与高相等;②圆锥的高小于母线;③圆柱、圆锥、圆台的底面都是圆;④用一个平面去截圆锥,得到一个圆锥和一个圆台.A.0　　　　B.1　　　　C.2　　　　D.3【解析】选C.①②正确;③它们的底面为圆面,不正确;④用平行于圆锥底面的平面截圆锥,可以得到一个圆锥和一个圆台.综上知选C.
2.球的直径有(　　)A.一条B.两条C.三条D.无数条【解析】选D.经过球心且端点在球面上的线段都是球的直径,则球有无数条直径.
3.圆台两底半径分别是2 cm和5 cm,母线长3 cm,则它的轴截面的面积为______. 【解析】画出轴截面,如图,过点A作AM⊥BC于点M,则BM=5-2=3,AM= =9,所以S四边形ABCD= =63(cm2). 答案:63 cm2
4.指出如图①②所示的图形是由哪些简单几何体构成的.