高中数学8.1 基本立体图形评课课件ppt

这是一份高中数学8.1 基本立体图形评课课件ppt，共41页。PPT课件主要包含了必备知识生成，平面多边形，公共边，一条定直线，这条定直线，四边形，两个互相平行的面，全等的多边形，其余各面，平行四边形等内容，欢迎下载使用。
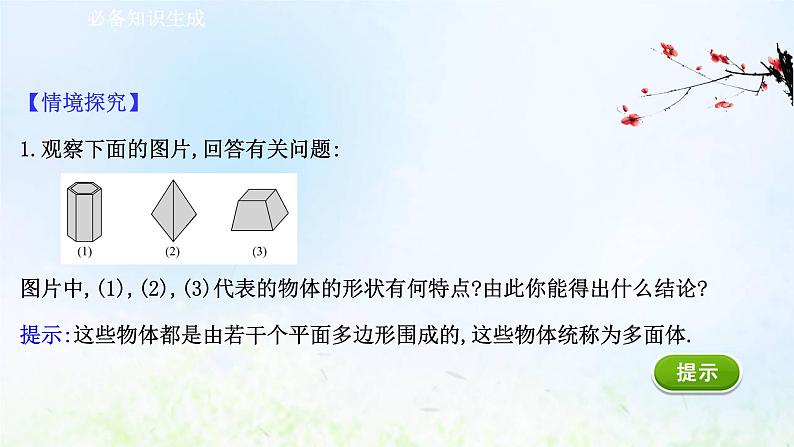
【情境探究】1.观察下面的图片,回答有关问题: 图片中,(1),(2),(3)代表的物体的形状有何特点?由此你能得出什么结论?提示:这些物体都是由若干个平面多边形围成的,这些物体统称为多面体.
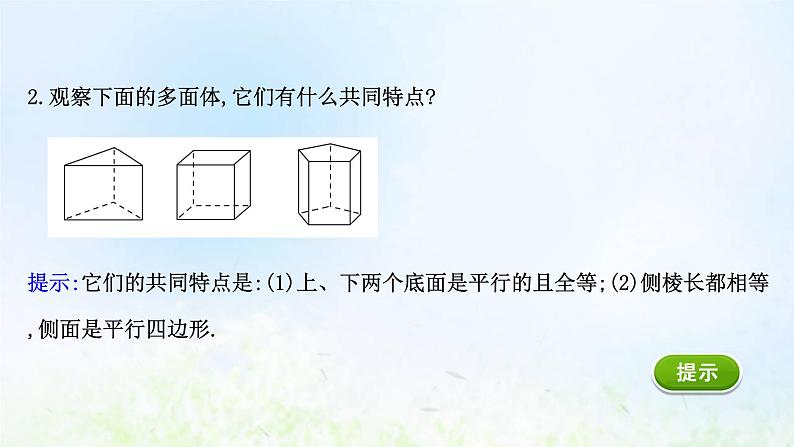
2.观察下面的多面体,它们有什么共同特点? 提示:它们的共同特点是:(1)上、下两个底面是平行的且全等;(2)侧棱长都相等,侧面是平行四边形.
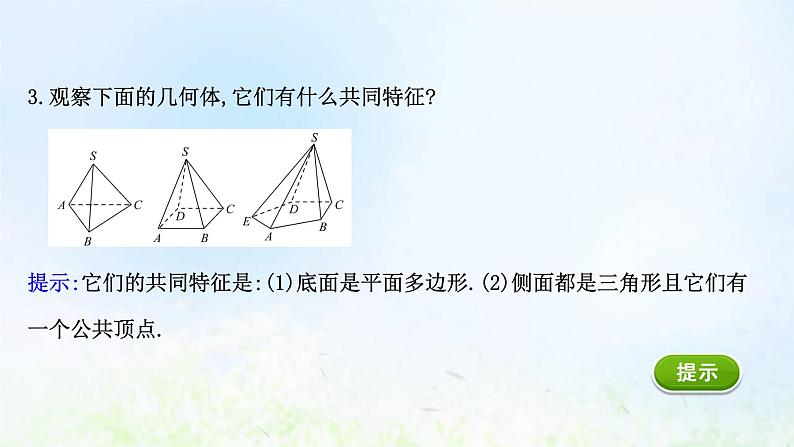
3.观察下面的几何体,它们有什么共同特征? 提示:它们的共同特征是:(1)底面是平面多边形.(2)侧面都是三角形且它们有一个公共顶点.
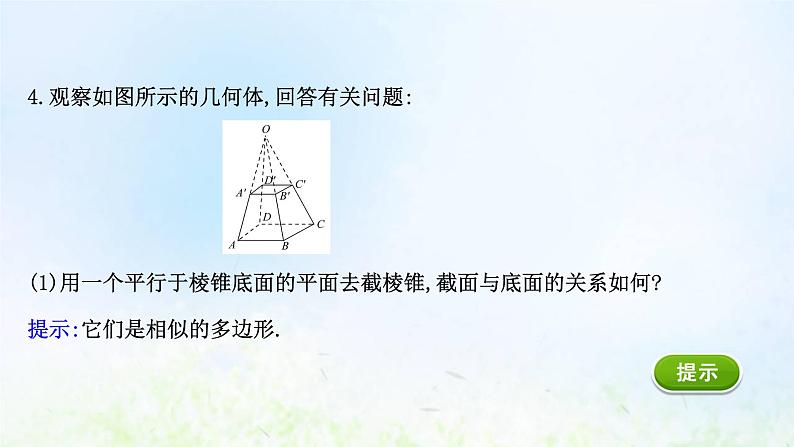
4.观察如图所示的几何体,回答有关问题: (1)用一个平行于棱锥底面的平面去截棱锥,截面与底面的关系如何?提示:它们是相似的多边形.
(2)图中几何体A′B′C′D′-ABCD是如何得来的?提示:几何体A′B′C′D′-ABCD是由一个平行于棱锥底面的平面去截棱锥所得到的.
【知识生成】1.多面体的有关概念:(1)定义:一般地,由若干个___________围成的几何体叫做多面体.(2)各部分名称:①面:围成多面体的各个多边形;②棱:相邻两个面的_______;③顶点:棱与棱的公共点.
2.旋转体的有关概念:(1)定义:一条平面曲线(包括直线)绕它所在平面内的___________旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体.(2)轴:___________.3.棱柱的有关概念(1)定义:一般地,有两个面互相_____,其余各面都是_______,并且相邻两个_______的公共边都互相_____,由这些面所围成的多面体叫做棱柱.
(2)有关概念: ①底面:_________________且是_____________;②侧面:_________且都是___________;③侧棱:_________________;④顶点:_____________________.
(3)特殊的棱柱:①直棱柱:侧棱_______底面的棱柱.②斜棱柱:侧棱_________底面的棱柱.③正棱柱:底面是_________的直棱柱.④平行六面体:底面是___________的四棱柱.
探究点一　空间几何体概念的理解与应用　　　　　　　　　　　　　　　　　　　【典例1】(1)下列关于棱柱的说法中正确的是(　　)A.棱柱的侧面是平行四边形,但它的底面一定不是平行四边形B.棱柱的一条侧棱的长叫做棱柱的高C.棱柱的两个互相平行的平面一定是棱柱的底面D.棱柱的所有面中,至少有两个面互相平行
(2)由5个面围成的多面体,其中上、下两个面是相似三角形,其余三个面都是梯形,并且这些梯形的腰延长后能相交于一点,则该多面体是(　　)A.三棱柱B.三棱台C.三棱锥D.四棱锥
【思维导引】根据棱柱、棱锥、棱台的结构特征判断.【解析】(1)选D.由棱柱的定义,知A不正确,例如长方体;只有直棱柱才满足选项B的条件,故B不正确;C不正确,例如正六棱柱的相对侧面互相平行;D显然正确.(2)选B.根据棱台的定义可判断该多面体为三棱台.
【类题通法】关于棱锥、棱台结构特征题目的判断方法(1)举反例法结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.
【定向训练】1.下列说法正确的是(　　)A.棱柱的底面一定是平行四边形B.棱锥的底面一定是三角形C.棱柱中两个互相平行的平面一定是棱柱的底面D.棱柱被平面分成的两部分可以都是棱柱
【解析】选D.棱柱、棱锥的底面可以是任意多边形,所以排除A、B.棱柱中两个互相平行的平面不一定是棱柱的底面,例如底面为正六边形的棱柱的相对侧面互相平行,排除C.对于D,只要这个平面与底面平行就能够得到两个棱柱.
2.有下列三个说法.①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.其中正确的有(　　)A.0个B.1个C.2个D.3 个
【解题指南】棱台的基本特点是上、下底面平行且相似,棱或母线延长后交于一点,这是判断几何体是否为棱台的依据.【解析】选A.关键是把握棱台的特点.①中的平面不一定平行于底面,故①错;②③可举反例去检验,如图,故②③错.
探究点二　几何体的结构特征【典例2】如图,E,F分别是正方形ABCD的边BC,CD的中点,沿图中虚线折起来,它能围成怎样的几何体?
【思维导引】三棱锥的三条侧棱交于同一点,由于E、F都是边的中点,所以折起后D,C,B会交于同一点.【解析】如图,折起围成一个三棱锥.
【类题通法】1.判断一个几何体是否为棱柱的三个关键(1)有两个面互相平行;(2)其余各面都是四边形;(3)每相邻两个四边形的公共边都互相平行.
2.判断一个几何体是否为棱锥的三个关键(1)底面是多边形.(2)侧面是三角形.(3)侧面有公共顶点.3.判断一个几何体是否为棱台的三个关键(1)两底面相互平行且相似.(2)各侧棱延长后交于一点.(3)侧面是梯形.
【定向训练】1.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是(　　) A.三棱锥B.四棱锥C.三棱柱D.组合体【解析】选B.余下部分是四棱锥A′-BCC′B′.
2.如图,四棱柱ABCD?A′B′C′D′,E,F分别为DD′,A′D′的中点,平面B′CEF截四棱柱ABCD?A′B′C′D′为两部分,则两部分是怎样的几何体?
【解析】多面体AA′FED-B′BC不是简单几何体,几何体B′C′C -FD′E是三棱台,其中△B′C′C和△FD′E是三棱台的底面.
探究点三　多面体的展开图【典例3】(1)一正方体的六个面上用记号笔分别标记了一个字,已知其表面展开图如图所示,则在原正方体中,互为对面的是(　　) A.聚与口,少与会,戴与罩B.聚与戴,口与会,少与罩C.聚与口,少与罩,戴与会D.聚与戴,口与罩,少与会
(2)如图是三个几何体的平面展开图,请问各是什么几何体?
【思维导引】(1)以其中一个面不动把其他面折叠⇒原正方体.(2)常见几何体的定义与结构特征⇒空间想象或动手制作平面展开图进行实践.
【解析】(1)选B.以戴为底,折叠正方体后,即可判断出:聚与戴,口与会,少与罩互为对面.(2)图①中,有5个平行四边形,而且还有两个全等的五边形,符合棱柱特点;图②中,有5个三角形,且具有共同的顶点,还有一个五边形,符合棱锥特点;图③中,有3个梯形,且其腰的延长线交于一点,还有两个相似的三角形,符合棱台的特点.把平面展开图还原为原几何体,如图所示:所以①为五棱柱,②为五棱锥,③为三棱台.
【类题通法】立体图形的展开或平面图形的折叠是培养空间想象能力的有效途径,解此类问题可以结合常见几何体的定义与结构特征,进行空间想象,或亲自动手制作平面展开图进行实践.
【定向训练】1.下图中不是正方体表面展开图的是(　　) 【解析】选C.把题目的表面展开图还原,可知C错.
2.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
【解析】将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图所示,线段AA1的长为所求△AEF周长的最小值.因为∠AVB=∠A1VC=∠BVC=30°,所以∠AVA1=90°.又VA=VA1=4,所以AA1=4 .所以△AEF周长的最小值为4 .
1.数学抽象：棱柱、棱锥、棱台的几何结构特征；2.逻辑推理：从实物中概括出棱柱、棱锥、棱台的几何结构特征；3..直观想象：棱柱、棱锥、棱台的分类；
注意概念中的特殊字眼，如棱柱的概念中的“相邻”，棱锥的概念中的“公共顶点”，棱台的概念中的“棱锥”“平行”等．
判断一个几何体是哪种几何体，一定要紧扣棱柱、棱锥、棱台的结构特征，弄清它们的内涵和外延。
1.在三棱锥A-BCD中,可以当作棱锥底面的三角形的个数为(　　)A.1个　　　B.2个　　　C.3个　　　D.4个【解析】选D.每个三角形都可以作为底面.
2.有两个面平行的多面体不可能是(　　)A.棱柱B.棱锥C.棱台D.长方体【解析】选B.棱锥的任意两个面都相交,不可能有两个面平行,所以不可能是棱锥.
3.下列图形经过折叠可以围成一个棱柱的是(　　) 【解析】选D.A,B,C中底面多边形的边数与侧面数不相等.