人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直随堂练习题

这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直随堂练习题，共9页。
一、选择题(每小题5分，共20分)
1．如图，在长方体ABCD­A1B1C1D1的棱中，与棱AB垂直的棱有( )
A.2条 B．4条 C．6条 D．8条
【解析】选D.在长方体ABCD­A1B1C1D1的棱中，与棱AB垂直的棱有BC，B1C1，A1D1，AD，AA1，BB1，CC1，DD1，共8条．
2．空间四边形ABCD中，E，F分别为AC，BD中点，若CD＝2AB，EF⊥AB，则EF与CD所成的角为( )
A.30° B．45° C．60° D．90°
【解析】选A.取AD的中点H，连接FH，EH，EH∥CD，FH∥AB，则在△EFH中∠EFH＝90°，
HE＝2HF，从而∠FEH＝30°.
3．在正三棱柱ABC­A1B1C1中，若AB＝ eq \r(2) BB1，则AB1与BC1所成的角的大小是( )
A.60° B．75° C．90° D．105°
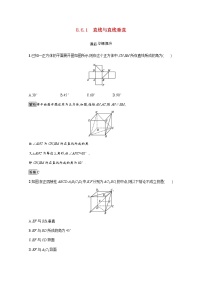
【解析】选C.设BB1＝1，
如图，延长CC1至C2，使C1C2＝CC1＝1，连接B1C2，则B1C2∥BC1，所以∠AB1C2为AB1与BC1所成的角(或其补角).连接AC2，因为AB1＝ eq \r(3) ，B1C2＝ eq \r(3) ，AC2＝ eq \r(6) ，所以AC eq \\al(\s\up1(2),\s\d1(2)) ＝AB eq \\al(\s\up1(2),\s\d1(1)) ＋B1C eq \\al(\s\up1(2),\s\d1(2)) ，则∠AB1C2＝90°.
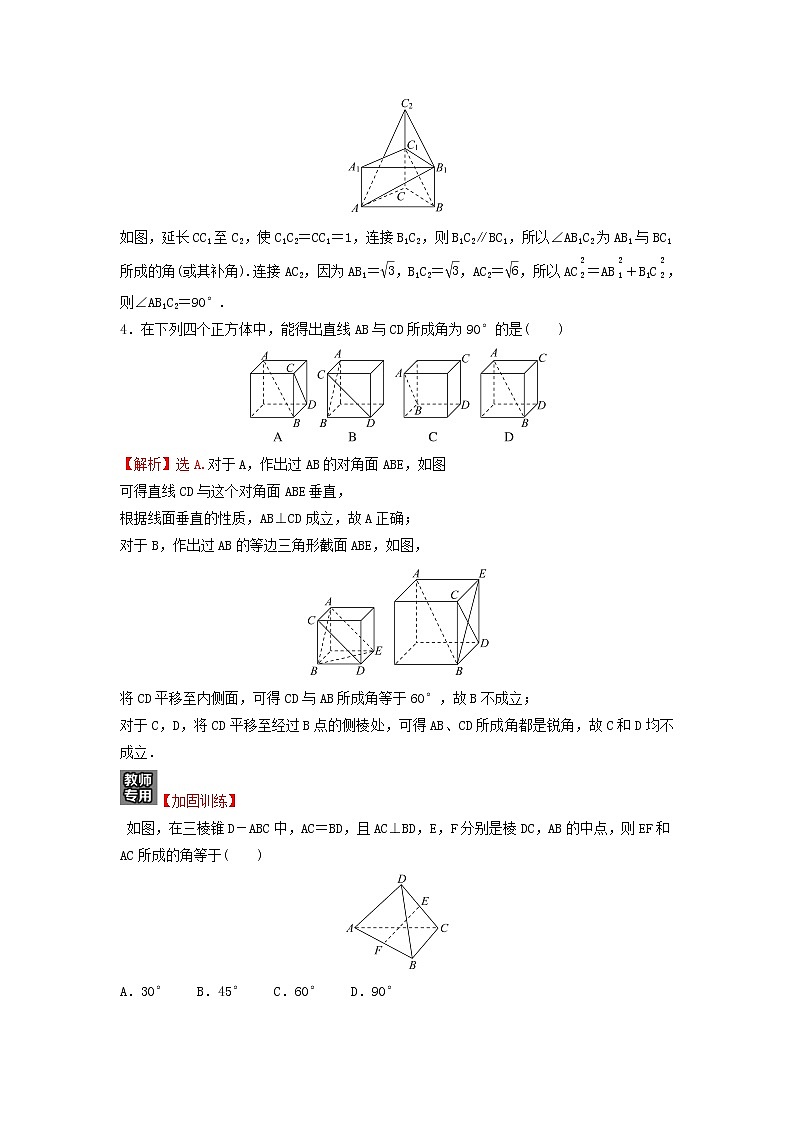
4．在下列四个正方体中，能得出直线AB与CD所成角为90°的是( )
【解析】选A.对于A，作出过AB的对角面ABE，如图
可得直线CD与这个对角面ABE垂直，
根据线面垂直的性质，AB⊥CD成立，故A正确；
对于B，作出过AB的等边三角形截面ABE，如图，
将CD平移至内侧面，可得CD与AB所成角等于60°，故B不成立；
对于C，D，将CD平移至经过B点的侧棱处，可得AB、CD所成角都是锐角，故C和D均不成立．
【加固训练】
如图，在三棱锥D－ABC中，AC＝BD，且AC⊥BD，E，F分别是棱DC，AB的中点，则EF和AC所成的角等于( )

A．30° B．45° C．60° D．90°
【解析】选B.如图所示，取BC的中点G，连接FG，EG.
因为E，F分别为CD，AB的中点，所以FG∥AC，EG∥BD，且FG＝ eq \f(1,2) AC，EG＝ eq \f(1,2) BD.
因为AC＝BD，所以FG＝EG，
所以∠EFG(或其补角)为EF与AC所成的角．
因为AC⊥BD，所以FG⊥EG，所以∠FGE＝90°，所以△EFG为等腰直角三角形．
所以∠EFG＝45°即EF与AC所成的角为45°.
二、填空题(每小题5分，共10分)
5．如图，在三棱柱ABC­A1B1C1中，AA1⊥平面ABC，四边形BCC1B1为正方形，BC＝2AB＝4，AB⊥BC，D为C1B1的中点，则异面直线A1C1与AD所成角的余弦值为________．
【解析】如图，过点D作DF∥A1C1，交A1B1于点F，连接AF，
则∠ADF为异面直线A1C1与AD所成角(或所成角的补角)，
因为在三棱柱ABC­A1B1C1中，AA1⊥平面ABC，四边形BCC1B1为正方形，BC＝2AB＝4，AB⊥BC，D为C1B1的中点，所以由题意知AD＝ eq \r(22＋22＋42) ＝2 eq \r(6) ，
DF＝ eq \r(12＋22) ＝ eq \r(5) ，AF＝ eq \r(42＋12) ＝ eq \r(17) ，
所以异面直线A1C1与AD所成角的余弦值为
cs ∠ADF＝ eq \f(AD2＋DF2－AF2,2×AD×DF) ＝ eq \f(24＋5－17,2×2\r(6)×\r(5)) ＝ eq \f(\r(30),10) ，所以异面直线A1C1与AD所成角的余弦值为 eq \f(\r(30),10) .
答案： eq \f(\r(30),10)
6．如图所示，已知正方体ABCD­A1B1C1D1中，E，F分别是AD，AA1的中点．
(1)直线AB1和CC1所成的角为________；
(2)直线AB1和EF所成的角为________．
【解析】如图．(1)因为BB1∥CC1，所以∠AB1B(或其补角)即为异面直线AB1与CC1所成的角，∠AB1B＝45°.
答案：45°
(2)连接B1C，AC易得EF∥B1C，所以∠AB1C(或其补角)即为异面直线AB1和EF所成的角．
连接AC，则△AB1C为正三角形，
所以∠AB1C＝60°.
答案：60°
三、解答题(每小题10分，共20分)
7．(2021·浦东高一检测)如图，直三棱柱A1B1C1­ABC中，AB＝AC＝1，∠BAC＝ eq \f(π,2) ，A1A＝4，点M为线段A1A的中点．
(1)求直三棱柱A1B1C1­ABC的体积；
(2)求异面直线BM与B1C1所成的角的余弦值．
【解析】(1)因为S△ABC＝ eq \f(1,2) ×1×1＝ eq \f(1,2) ，
所以V＝S△ABC·A1A＝ eq \f(1,2) ×4＝2.
(2)连接MC.因为BC∥B1C1，所以∠MBC或其补角是异面直线BM与B1C1所成的角，在△MBC中，BM＝CM＝ eq \r(5) ，BC＝ eq \r(2) ，
由余弦定理得，cs ∠MBC＝ eq \f(BM2＋BC2－CM2,2BM·BC) ＝ eq \f(\r(10),10) .
8．如图，已知在长方体ABCD­A1B1C1D1中，A1A＝AB，E，F分别是BD1和AD的中点，求证：CD1⊥EF.
【证明】取CD1的中点G，连接EG，DG.
因为E是BD1的中点，所以EG∥BC，EG＝ eq \f(1,2) BC.
因为F是AD的中点，且AD∥BC，AD＝BC，
所以DF∥BC，DF＝ eq \f(1,2) BC，所以EG∥DF，EG＝DF，
所以四边形EFDG是平行四边形，所以EF∥DG，
所以∠DGD1(或其补角)是异面直线CD1与EF所成的角．又A1A＝AB，
所以四边形ABB1A1，四边形CDD1C1都是正方形，且G为CD1的中点，所以DG⊥CD1，
所以∠D1GD＝90°，所以CD1⊥EF.
【综合突破练】 (20分钟 40分)
一、选择题(每小题5分，共10分)
1．(2021·汾阳高一检测)如图，在棱长均为2的四棱锥S­ABCD中，E为SB的中点，则异面直线AE与BC所成角的余弦值为( )
A. eq \f(\r(3),3) B． eq \f(\r(3),6) C． eq \f(2\r(15),15) D． eq \f(3\r(5),10)
【解析】选B.连接DE，BD，
由题意知，四棱锥S­ABCD为正四棱锥，
所以AD∥BC，所以∠DAE即为异面直线AE与BC所成角，
因为SB＝SD＝2，BD＝2 eq \r(2) ，
所以SB2＋SD2＝BD2，即SB⊥SD，
所以DE＝ eq \r(SD2＋SE2) ＝ eq \r(4＋1) ＝ eq \r(5) ，
在△ADE中，AD＝2，AE＝ eq \r(3) ，DE＝ eq \r(5) ，
由余弦定理知，cs ∠DAE＝ eq \f(AD2＋AE2－DE2,2AD·AE)
＝ eq \f(4＋3－5,2×2×\r(3)) ＝ eq \f(\r(3),6) ，
所以异面直线AE与BC所成角的余弦值为 eq \f(\r(3),6) .
2．(多选题)(2021·海口高一检测)如图，在正四棱柱ABCD­A1B1C1D1中，AB＝ eq \r(2) AA1，E，F分别为AB，BC的中点，异面直线AB1与C1F所成角的余弦值为m，则( )
A.m＝ eq \f(\r(3),3)
B．直线A1E与直线C1F共面
C．m＝ eq \f(\r(2),3)
D．直线A1E与直线C1F异面
【解析】选BC.如图，连接DC1，DF，则DC1∥AB1，
所以∠DC1F为异面直线AB1与C1F所成的角，
因为AB＝ eq \r(2) AA1，ABCD­A1B1C1D1为正四棱柱，E，F分别为AB，BC的中点，
设AA1＝ eq \r(2) ，
则AB＝2，C1D＝ eq \r(6) ，C1F＝ eq \r(3) ，DF＝ eq \r(5) ，
所以在△DFC1中，
根据余弦定理，
cs ∠DC1F＝ eq \f(6＋3－5,2×\r(6)×\r(3)) ＝ eq \f(\r(2),3) ，
所以m＝ eq \f(\r(2),3) ；
连接A1C1，AC，EF，则A1C1∥AC，EF∥AC，
所以EF∥A1C1，所以A1E与C1F共面．
二、填空题(每小题5分，共10分)
3．如图，直四棱柱ABCD­A1B1C1D1，底面是边长为a的菱形，∠BAD＝60°，AA1＝2a，则直线A1C1与B1C成角的余弦值为________．
【解析】连接AC，AB1，
因为直四棱柱ABCD­A1B1C1D1中A1C1∥AC，
所以∠ACB1是直线A1C1与B1C成角(或所成角的补角).
因为底面是边长为a的菱形，∠BAD＝60°，
所以AC＝ eq \r(a2＋a2－2×a×a×cs 120°)
＝ eq \r(3) a，
因为AA1＝2a，所以AB1＝CB1＝ eq \r(a2＋（2a）2) ＝ eq \r(5) a，
所以cs ∠ACB1＝ eq \f(（\r(3)a）2＋（\r(5)a）2－（\r(5)a）2,2×\r(3)a×\r(5)a) ＝ eq \f(\r(15),10) .
故直线A1C1与B1C成角的余弦值为 eq \f(\r(15),10) .
答案： eq \f(\r(15),10)
4．如图所示，在等边三角形ABC中，D，E，F分别为各边中点，G，H，I，J分别为AF，AD，BE，DE的中点．将△ABC沿DE，EF，DF折成三棱锥后，GH与IJ所成角的度数为________．
【解析】将三角形折成三棱锥，如图所示，
GH与IJ为异面直线，在三棱锥A­DEF中，IJ eq \f(1,2) AD，GH eq \f(1,2) DF，所以∠ADF即为所求，
因此GH与IJ所成角为60°.
答案：60°
三、解答题(每小题10分，共20分)
5．在空间四边形ABCD中，两条对边AB＝CD＝3，E，F分别是另外两条对边AD，BC上的点，且 eq \f(AE,ED) ＝ eq \f(BF,FC) ＝ eq \f(1,2) ，EF＝ eq \r(5) ，求证：AB⊥CD.
【证明】如图，连接BD，过点E作AB的平行线交BD于点O，连接OF，EF.
因为EO∥AB且 eq \f(AE,ED) ＝ eq \f(1,2)
所以 eq \f(EO,AB) ＝ eq \f(2,3) .
因为AB＝3，所以EO＝2.
又 eq \f(BF,FC) ＝ eq \f(1,2) ，所以 eq \f(BF,FC) ＝ eq \f(BO,OD) ，
所以OF∥DC，所以OE与OF所成的角即为AB和CD所成的角，
因为DC＝3，所以OF＝1.
在△OEF中，OE2＋OF2＝5，EF2＝( eq \r(5) )2＝5，
所以OE2＋OF2＝EF2，所以∠EOF＝90°，所以AB⊥CD.
6．如图，在四棱柱ABCD­A1B1C1D1中，侧面都是矩形，底面四边形ABCD是菱形且AB＝BC＝2，∠ABC＝120°，若异面直线A1B和AD1所成的角为90°，试求AA1的长．
【解析】连接CD1，AC，
由题意得在四棱柱ABCD­A1B1C1D1中，
A1D1∥BC，A1D1＝BC，
所以四边形A1BCD1是平行四边形，
所以A1B∥CD1，所以∠AD1C(或其补角)为A1B和AD1所成的角．
因为异面直线A1B和AD1所成的角为90°，所以∠AD1C＝90°.
因为四棱柱ABCD­A1B1C1D1中，AB＝BC＝2，
所以△ACD1是等腰直角三角形，
所以AD1＝CD1.因为底面四边形ABCD是菱形，且AB＝BC＝2，∠ABC＝120°，
所以AC＝2×sin 60°×2＝2 eq \r(3) ，AD1＝CD1＝ eq \r(6) ，
在Rt△ADD1中，AA eq \\al(\s\up1(2),\s\d1(1)) ＝AD eq \\al(\s\up1(2),\s\d1(1)) －A1D eq \\al(\s\up1(2),\s\d1(1))
＝( eq \r(6) )2－22＝2.
所以AA1＝ eq \r(2) .