高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行课堂检测

这是一份高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行课堂检测，共7页。
一、选择题(每小题5分，共20分)
1．下列四面体中，直线EF与MN平行的是( )
【解析】选C.根据过平面内一点和平面外一点的直线，与平面内不过该点的直线异面，可判定A，B中EF，MN异面；C中直线EF与MN平行；
D中，若EF∥MN，则过EF的平面与底面相交，EF就跟交线平行，则过点N有两条直线与EF平行，不可能．
2．如图，在正方体ABCD­A1B1C1D1中，E，F，G，H，M，N分别是棱AB，BC，A1B1，BB1，C1D1，CC1的中点，则下列结论正确的是( )
A.直线GH和MN平行，GH和EF相交
B．直线GH和MN平行，MN和EF相交
C．直线GH和MN相交，MN和EF异面
D．直线GH和EF异面，MN和EF异面
【解析】选B.易知GH∥MN，又因为E，F，M，N分别为所在棱的中点，由平面基本性质3可知EF，DC，MN交于一点．
3．在正方体ABCD­A1B1C1D1中，E，F分别是平面AA1D1D，平面CC1D1D的中心，G，H分别是边AB，BC的中点，则直线EF与直线GH的位置关系是( )
A．相交 B．异面 C．平行 D．垂直
【解析】选C.如图，连接AD1，CD1，AC，则E，F分别为AD1，CD1的中点．由三角形的中位线定理，知EF∥AC，GH∥AC，所以EF∥GH，故选C.
4．(2021·鄂州高一检测)若异面直线a，b分别在平面α，β内，且α∩β＝l，则直线l( )
A．与直线a，b都相交
B．至少与a，b中的一条相交
C．至多与a，b中的一条相交
D．与a，b中的一条相交，另一条平行
【解析】选B.由题意知：直线l与a，b可都相交，也可只与一条相交，故A、C、D错误；
但直线l不会与两条都不相交，
若l与a，b都不相交，因为l与a都在α内，
所以l∥a，同理l∥b，所以a∥b，
这与a，b异面直线矛盾，
故直线l至少与a，b中之一相交．故B正确．
二、填空题(每小题5分，共10分)
5．已知棱长为a的正方体ABCD­A′B′C′D′中，M，N分别为CD，AD的中点，则MN与A′C′的位置关系是________．
【解析】MN eq \f(1,2) AC，又因为ACA′C′，
所以MN eq \f(1,2) A′C′.
答案：平行
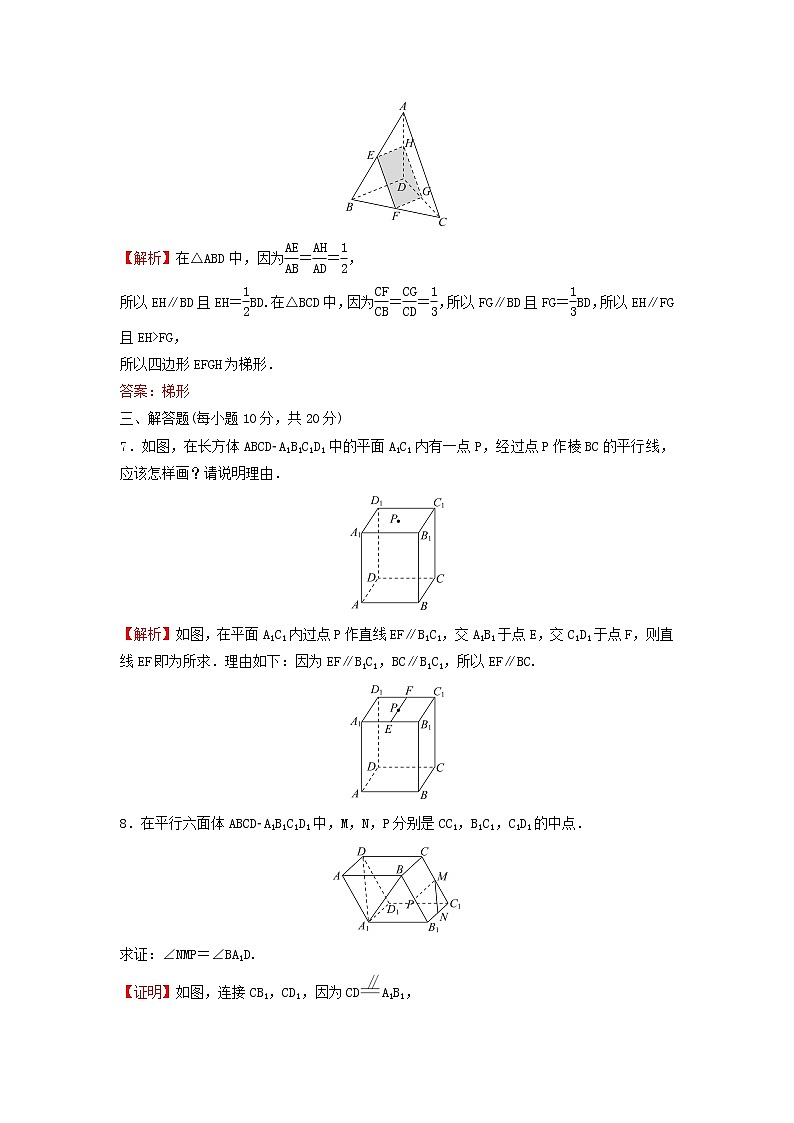
6．已知E，F，G，H为空间四边形ABCD的边AB，BC，CD，DA上的点，若 eq \f(AE,AB) ＝ eq \f(AH,AD) ＝ eq \f(1,2) ， eq \f(CF,CB) ＝ eq \f(CG,CD) ＝ eq \f(1,3) ，则四边形EFGH形状为________．
【解析】在△ABD中，因为 eq \f(AE,AB) ＝ eq \f(AH,AD) ＝ eq \f(1,2) ，
所以EH∥BD且EH＝ eq \f(1,2) BD.在△BCD中，因为 eq \f(CF,CB) ＝ eq \f(CG,CD) ＝ eq \f(1,3) ，所以FG∥BD且FG＝ eq \f(1,3) BD，所以EH∥FG且EH>FG，
所以四边形EFGH为梯形．
答案：梯形
三、解答题(每小题10分，共20分)
7．如图，在长方体ABCD­A1B1C1D1中的平面A1C1内有一点P，经过点P作棱BC的平行线，应该怎样画？请说明理由．
【解析】如图，在平面A1C1内过点P作直线EF∥B1C1，交A1B1于点E，交C1D1于点F，则直线EF即为所求．理由如下：因为EF∥B1C1，BC∥B1C1，所以EF∥BC.
8．在平行六面体ABCD­A1B1C1D1中，M，N，P分别是CC1，B1C1，C1D1的中点．
求证：∠NMP＝∠BA1D.
【证明】如图，连接CB1，CD1，因为CDA1B1，
所以四边形A1B1CD是平行四边形．
所以A1D∥B1C.因为M，N分别是CC1，B1C1的中点，所以MN∥B1C，
所以MN∥A1D.因为BCA1D1，
所以四边形A1BCD1是平行四边形，
所以A1B∥CD1.
因为M，P分别是CC1，C1D1的中点，
所以MP∥CD1，所以MP∥A1B，
因为∠NMP和∠BA1D的两边分别平行且方向都相反，所以∠NMP＝∠BA1D.
【综合突破练】 (20分钟 40分)
一、选择题(每小题5分，共10分)
1．已知在空间四边形ABCD中，若M，N分别是AB，CD的中点，且AC＝4，BD＝6，则( )
A．1