数学第八章 立体几何初步8.5 空间直线、平面的平行课时训练

这是一份数学第八章 立体几何初步8.5 空间直线、平面的平行课时训练，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(每小题5分，共20分)
1．平面α截一个三棱锥，如果截面是梯形，那么平面α必定和这个三棱锥的( )
A.一个侧面平行 B．底面平行
C．仅一条棱平行 D．某两条相对的棱都平行
【解析】选C.当平面α∥平面ABC时，如图(1)所示，截面是三角形，不是梯形，所以A，B不正确；
当平面α∥SA时，如图(2)所示，此时截面是四边形DEFG.又SA⊂平面SAB，平面SAB∩α＝DG，
所以SA∥DG.同理SA∥EF，所以EF∥DG.
同理，当平面α∥BC时，GF∥DE，但是截面是梯形，则四边形DEFG中仅有一组对边平行，所以平面α仅与一条棱平行．所以D不正确，C正确．
2．(多选题)如图是正方体的平面展开图，在这个正方体中，下列命题中，正确的有( )
A．BM∥平面DCMN
B．CN∥平面BCMF
C．平面BDM∥平面AFN
D．平面BDE∥平面NCF
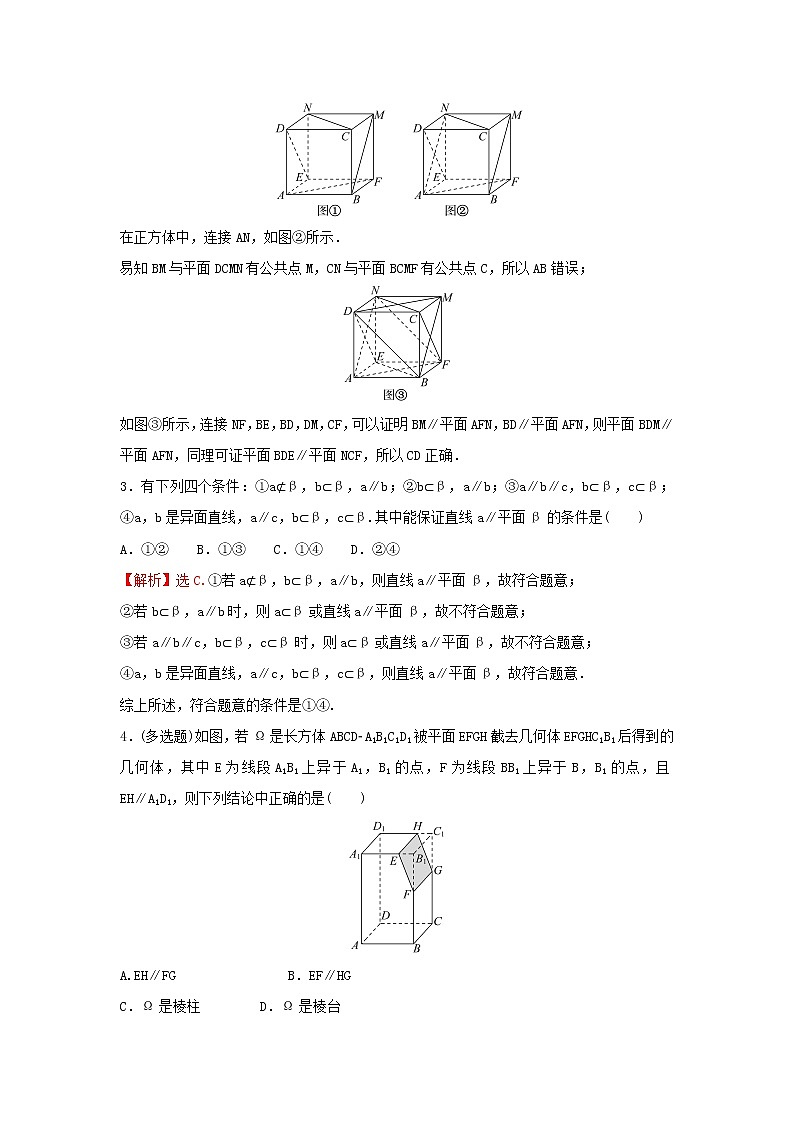
【解析】选CD.展开图可以折成如图①所示的正方体．
在正方体中，连接AN，如图②所示．
易知BM与平面DCMN有公共点M，CN与平面BCMF有公共点C，所以AB错误；
如图③所示，连接NF，BE，BD，DM，CF，可以证明BM∥平面AFN，BD∥平面AFN，则平面BDM∥平面AFN，同理可证平面BDE∥平面NCF，所以CD正确．
3．有下列四个条件：①a⊄β，b⊂β，a∥b；②b⊂β，a∥b；③a∥b∥c，b⊂β，c⊂β；④a，b是异面直线，a∥c，b⊂β，c⊂β.其中能保证直线a∥平面β的条件是( )
A．①② B．①③ C．①④ D．②④
【解析】选C.①若a⊄β，b⊂β，a∥b，则直线a∥平面β，故符合题意；
②若b⊂β，a∥b时，则a⊂β或直线a∥平面β，故不符合题意；
③若a∥b∥c，b⊂β，c⊂β时，则a⊂β或直线a∥平面β，故不符合题意；
④a，b是异面直线，a∥c，b⊂β，c⊂β，则直线a∥平面β，故符合题意．
综上所述，符合题意的条件是①④.
4．(多选题)如图，若Ω是长方体ABCD­A1B1C1D1被平面EFGH截去几何体EFGHC1B1后得到的几何体，其中E为线段A1B1上异于A1，B1的点，F为线段BB1上异于B，B1的点，且EH∥A1D1，则下列结论中正确的是( )
A.EH∥FG B．EF∥HG
C．Ω是棱柱 D．Ω是棱台
【解析】选ABC.因为EH∥A1D1，A1D1∥B1C1，
所以EH∥B1C1，
又EH⊄平面BCC1B1，B1C1⊂平面BCC1B1，
所以EH∥平面BCC1B1，
又EH⊂平面EFGH，
平面EFGH∩平面BCC1B1＝FG，
所以EH∥FG，故EH∥FG∥B1C1，
所以选项A，C正确，D错误；
因为平面ABB1A1∩平面EFGH＝EF，
平面CDD1C1∩平面EFGH＝GH，
平面ABB1A1∥平面CDD1C1，
所以EF∥GH，故B正确．
二、填空题(每小题5分，共10分)
5．如图，在直三棱柱ABC­A1B1C1中，∠BAC＝ eq \f(π,2) ，AA1＝AB＝AC＝1，CC1的中点为H，点N在棱A1B1上，HN∥平面A1BC，则 eq \f(A1N,A1B1) 的值为________．
【解析】如图，
取A1C1的中点M，A1B1的中点N1，连接HM，MN1，
由H，M，N1分别为CC1，A1C1，A1B1的中点，
得MH∥A1C，MN1∥B1C1∥BC.
因为A1C⊂平面A1BC，MH⊄平面A1BC，
所以MH∥平面A1BC；
因为BC⊂平面A1BC，MN1⊄平面A1BC，
所以MN1∥平面A1BC，
又MH∩MN1＝M，
所以平面MN1H∥平面A1BC，
则N1H∥平面A1BC.
故当N1与N重合时，HN∥平面A1BC，
所以 eq \f(A1N,A1B1) 的值为 eq \f(1,2) .
答案： eq \f(1,2)
6．如图所示，在正方体ABCD­A1B1C1D1中，E，F，G，H分别为棱CC1，C1D1，D1D，CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，若MN∥平面B1BDD1，则点M的轨迹是________．
【解析】连接FH，FN.因为FH∥BB1，HN∥BD，FH∩HN＝H，
所以平面FHN∥平面B1BDD1，
又平面FHN∩平面EFGH＝FH，
所以当M∈FH时，MN⊂平面FHN，
所以MN∥平面B1BDD1.
答案：线段FH
三、解答题(每小题10分，共20分)
7．如图所示的一块四棱柱木料ABCD­A1B1C1D1，底面ABCD是梯形，且CD∥AB.
(1)要经过面A1B1C1D1内的一点P和侧棱DD1将木料锯开，应怎样画线？
(2)所画的线之间有什么位置关系？
【解析】(1)如图所示，连接D1P并延长交A1B1于E，过E作EF∥AA1交AB于F，连接DF，
则D1E，EF，FD就是应画的线．
(2)因为DD1∥AA1，EF∥AA1，所以D1D∥EF.
所以D1D与EF确定一个平面α.
又因为平面AC∥平面A1C1，α∩平面AC＝DF，
α∩平面A1C1＝D1E，所以D1E∥DF.
显然DF，D1E都与EF相交．
8．如图①，在直角梯形ABCP中，AP∥BC，AP⊥AB，AB＝BC＝ eq \f(1,2) AP，D为AP的中点，E，F，G分别为PC，PD，CB的中点，将△PCD沿CD折起，得到四棱锥P­ABCD，如图②.
求证：在四棱锥P­ABCD中，AP∥平面EFG.
【证明】在四棱锥P­ABCD中，E，F分别为PC，PD的中点，所以EF∥CD.
因为AB∥CD，所以EF∥AB.因为EF⊄平面PAB，AB⊂平面PAB，所以EF∥平面PAB.同理EG∥平面PAB.
又EF∩EG＝E，EF⊂平面EFG，EG⊂平面EFG，
所以平面EFG∥平面PAB.
因为AP⊂平面PAB，所以AP∥平面EFG.