新人教A版高中数学必修第二册第九章统计阶段复习课课件

这是一份新人教A版高中数学必修第二册第九章统计阶段复习课课件，共13页。

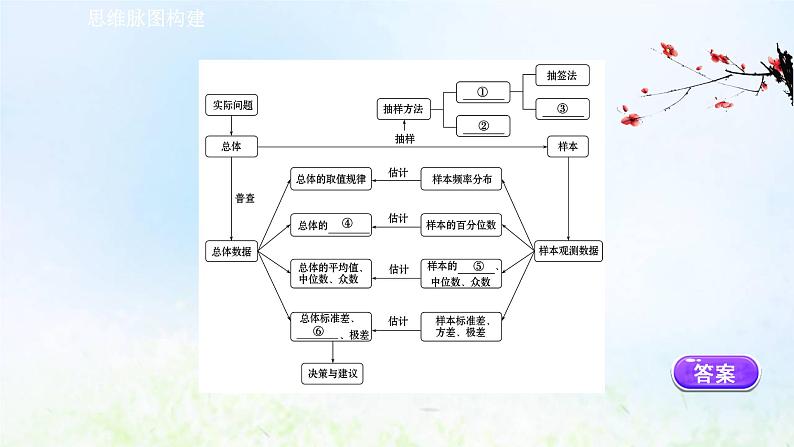
阶段复习课第四课　统　　计思维脉图构建【答案速填】①__简单随机抽样__ ②__分层随机抽样__ ③__随机数法__ ④__百分位数__ ⑤__平均数__ ⑥__方差__ 易错案例警示易错一　抽样不合理致误【案例1】某班有42名男生,30名女生,已知男女身高各有明显不同,现欲调查平均身高,若采用分层随机抽样方法,抽取男生1人,女生1人,这种做法是否合适,若不合适,应怎样抽取?【解析】考虑到本题应采用分层随机抽样及男、女生各自的人数,故按7∶5抽取更合适,即男生抽取7人,女生抽取5人,各自用抽签法或随机数法抽取组成样本.【错因探究】由于取样比例数过小,仅抽取2人,很难准确反映总体情况,又因为男、女生差异较大,抽取人数相同,也不尽合理,故此法不合适,抽取人数过多,失去了抽样调查的统计意义,取样太少,不能准确反映真实情况.【避错警示】抽取样本时,应尽可能反映总体的特征,根据具体的情况确定样本数,按照一定的抽样比进行分层抽取或利用简单随机抽样进行抽取.易错二　因不理解抽样方法的适用范围而致误【案例2】某学校附近的一家小型超市为了了解一年的客流量情况,决定用抽签法从一年中抽取52天作为样本实施调查(假设一年有52个星期),你觉得这样的选择合适吗?为什么?【解析】这种选择不合适. 应该将全年分为两层,放假(一般一年寒暑假放假共计10周)与上学(42周).每层用简单随机抽样的方法,抽取适当的样本进行调查.【错因探究】对于本题,产生错误的根源是没有弄清这家超市一年中的客流量变化情况.应该清楚这家超市位于学校附近,因此客流量受学生作息制度的影响较大.【避错警示】明确每一种抽样的使用范围和抽取方法,是避免出现类似错误的前提.一般来说,简单随机抽样要求总体中个体数目较少;分层随机抽样适用于总体由差异明显的几部分组成(即各部分层次性明显).易错三　分层随机抽样的平均数计算致误 【案例3】若 是x1,x2,…,x100的平均值,a1为x1,x2,…,x40的平均值,a2为x41,x42,…,x100的平均值,则下列式子中正确的是 (　　)【解析】选A.由于x1+x2+…+x100= ,而x1+x2+…+x40=40a1,x41+x42+…+x100=60a2,于是 【错因探究】对分层抽样得到的样本,各层抽取的个体个数一般不等,不能对各层得到的平均数进行简单地相加或取平均值.【避错警示】对于分别有m,n的两层数据平均数可以由下列公式计算样本平均数:数据x1,x2,…,xm的平均数为 ,数据y1,y2,…,yn的平均数为 ,易错四　公式使用不当致误【案例4】若10个正整数的平方和是208,平均数是4,则这组数据的方差为多少?将这组数据同时减去3,则新数据的平均数为多少?方差为多少?【解析】由方差公式 展开整理可得 这里由题设知n=10,所以 因为一组数据同时减去a后,平均数为( -a),方差不变,所以都减去3后,平均数为1,方差为4.8.【错因探究】对方差的意义理解不到位,公式记忆不准确导致本题计算错误.对于一组数据都减去或加上同一个数,方差不变.【避错警示】正确理解方差的概念与意义,方差所表达的是一组数据相对于取值平均水平的偏离(离散)程度.只有理解概念、熟记公式,才不至于出错.