数学七年级下册3 三角形的三边关系授课课件ppt

这是一份数学七年级下册3 三角形的三边关系授课课件ppt，共33页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，三角形的三边关系，三角形三边关系的应用，已知两边，第三边的范围等内容，欢迎下载使用。

三角形的三边关系三角形三边关系的应用三角形的稳定性
在很很久以前，欧几里得做了一个奇怪的梦，在梦里上帝要他利用长度是3、4、8的三条线段做一个美丽的三角形，欧几里得想啊，做啊，就是完不成这个任务，所以他也就一直睡醒，你能帮帮欧几里得，让他快的而醒来吗？
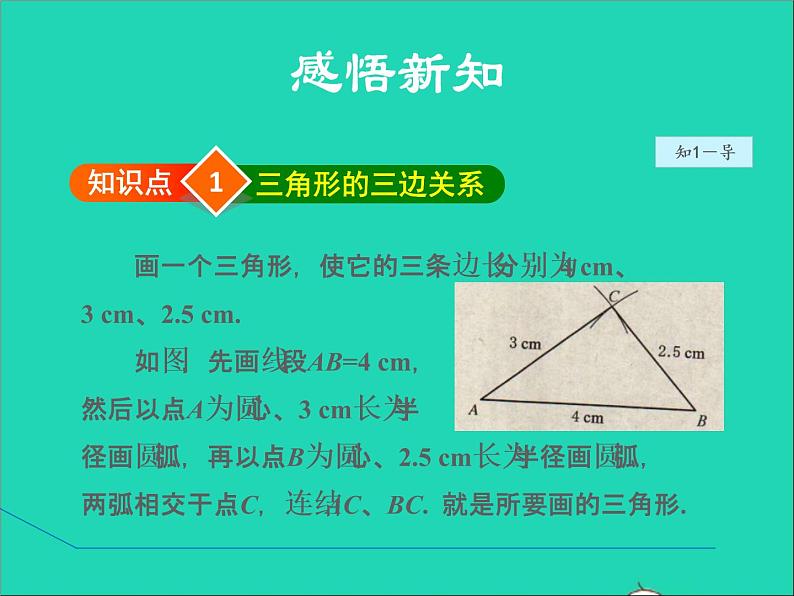
画一个三角形，使它的三条边长分别为4 cm、3 cm、2.5 cm. 如图，先画线段AB=4 cm，然后以点A为圆心、3 cm长为半径画圆弧，再以点B为圆心、2.5 cm长为半径画圆弧，两弧相交于点C，连结AC、BC. 就是所要画的三角形.
现有若干条已知长度的线段：三条长2 cm、三条长3 cm、两条长4 cm、两条长5 cm、两条长6 cm. 任意选择三条线段画三角形，使它的三条边长分别为你所选择的三条线段的长. 说说你的发现与想法.
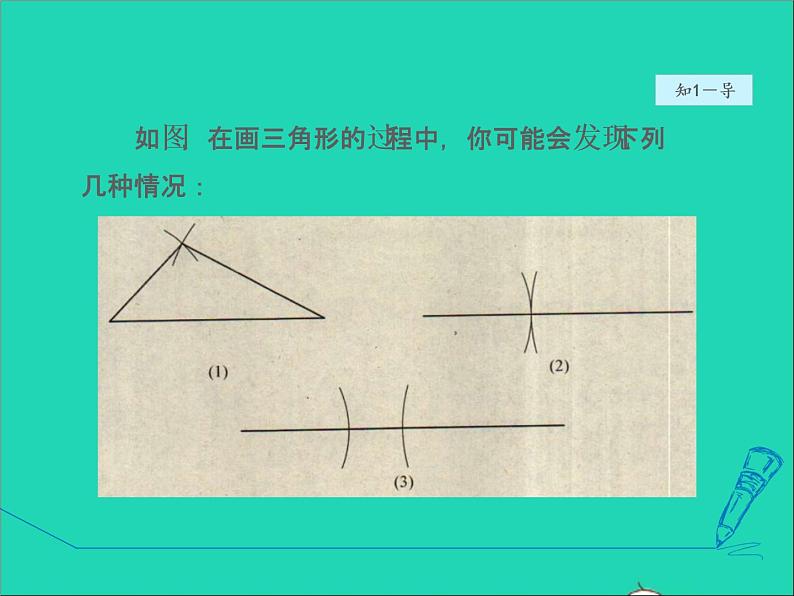
如图，在画三角形的过程中，你可能会发现下列几种情况：
因此，并不是任意三条线段都可以组成一个三角形. 在三条线段中，如果两条较短线段的和不大于第三条线 段，那么这三条线段就不能组成一个三角形. 换句话说： 三角形的任何两边的和大于第三边.
1. 三角形的三边关系：三角形的任何两边的和大于第 三边．利用此关系验证三条线段能否围成三角形时， 只要判断较短的两条线段的和是否大于最长的线段 即可．拓展：(1)三角形的任何两边的差小于第三边；(2)三角形第三边的取值范围：其他两边之差<第三边< 其他两边之和；(3)三角形三边关系的理论依据：两点之间线段最短．
下列各组线段中，不能组成三角形的一组是(　　)A．4 cm，7 cm，10 cm　　　　B．a＋1，a＋2，a＋3(a>0)C．3a，5a，2a＋1(a>0) D．三线段之比为1∶2∶3
组成三角形需满足三边关系，即较短的两条线段的和大于最长的线段．A选项中，4＋7>10，能组成三角形；B选项中，a＋1＋(a＋2)＝2a＋3>a＋3，能组成三角形；C选项中，3a＋2a＋1＝5a＋1>5a，能组成三角形；D选项中，设三线段分别为a，2a，3a，∵a＋2a＝3a，∴不能组成三角形．
要组成三角形，只要满足较短的两条线段的和大于最长的线段即可．
(温州)下列各组数可能是一个三角形的边长的是(　　)A．1，2，4 　B．4，5，9C．4，6，8 D．5，5，11(崇左)如果一个三角形的两边长分别为2和5，则第三边长可能是(　　)A．2 B．3C．5 D．8
(中考·长沙)若一个三角形的两边长分别为3和7，则第三边长可能是(　　)A．6 B．3 C．2 D．11(中考·岳阳)下列长度的三根小木棒能构成三角形的是(　　)A．2 cm，3 cm，5 cm B．7 cm，4 cm，2 cmC．3 cm，4 cm，8 cm D．3 cm，3 cm，4cm
要点精析：运用三角形的三边关系可以解决以下问题：(1)判断三条已知线段能否组成一个三角形；(2)已知三角形的两边长，确定第三边长的取值范围或 周长的取值范围；(3)当三角形的边长用字母表示时，确定字母的取值范 围；(4)证明一些线段的不等关系．
一个三角形两边的长分别为5 cm和3 cm，第三边的长是整数，且周长是偶数，则第三边的长是(　　)A．2 cm或4 cm 　 B．4 cm或6 cm　 C．4 cm　 D．2 cm或6 cm
要求第三边的长，需先求出这条边的范围，再在其范围内找出满足条件的数．设三角形第三边的长为x cm，则x的取值范围为5－3＜x＜5＋3，即2＜x＜8.又在2到8之间的整数有3，4，5，6，7，而三角形的周长x＋3＋5＝x＋8应为偶数，所以x也是偶数，所以x的值只能是4，6.所以三角形第三边的长是4 cm或6 cm.
通过多个条件确定三角形第三边的方法：
第三边小于其他两边的和而大于其他两边的差
用一条长为21 cm的细绳围成一个三角形，能围成一边长是5 cm的等腰三角形吗？为什么？
因为5 cm长的边可能是腰，也可能是底边，所以需要分情况讨论．
当5 cm长的边是底边时，设腰长为x cm，则 5＋2x＝21，解得x＝8.当5 cm长的边是腰时，设底边长为y cm，则 2×5＋y＝21，解得y＝11.因为5＋5<11，不符合三角形的两边之和大于第三边，所以不能围成腰长为5 cm的等腰三角形．所以能围成底边长为5 cm的等腰三角形．
本题运用了分类讨论思想，在考虑腰长和底边长两种情况的同时，要注意隐含的条件：任意两边之和大于第三边；解答这类题时，出现两种结果的较多，应高度重视．
一个三角形的两边长分别是3和7，且第三边的长是整数，这样的三角形中周长的最小值是多少？已知等腰三角形的两边长分别为4 cm和7 cm，且它的周长大于16 cm，则第三边长为________．已知三角形的三边长为连续整数，且周长为12 cm，则它的最短边长为(　　)A．2 cm B．3 cmC．4 cm D．5 cm
用三根木条钉一个三角形，你会发现再也无法改变这个三角形的形状和大小，也就是说，如果三角形的三条边固定，那么三角形的形状和大小就完全确定了. 三角形的这个性质叫做三角形的稳定性. 用四根木条钉一个四边形，你会发现这个四边形的形状和大小都可以改变，这说明四边形不具有稳定性.
三角形的稳定性在生产实践中有着广泛的应用. 例 如桥梁拉杆(如图所示)、电视塔架底座，都是三角形结构.
1. 如果三角形的三条边固定，那么三角形的形状和大 小就完全确定了．三角形的这个性质叫做三角形的 稳定性．2. 四边及四边以上的图形不具有稳定性，为保证其稳 定，常在多边形中构造三角形． 注意：稳定性是三角形的特性，其他图形都不具有 稳定性．
工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的依据是(　　)A．三角形的稳定性　　 B．两点之间线段最短C．两点确定一条直线 D．垂线段最短
本题主要考查三角形的稳定性在实际生活中的应用，工人师傅的这种做法是利用三角形的稳定性，避免门框变形．
本题是利用三角形的稳定性来克服四边形的不稳定性．
(探究题) 要使四边形木架(用四根木条钉成)不变形，至少要再钉上几根木条？五边形木架呢？六边形木架呢？n边形木架呢？
四边形木架至少要再钉上1根，五边形木架：2根，六边形木架：3根，n边形木架：(n－3)根．
若要多边形稳定，需将它变换成若干个三角形. 先画出图形，结合图形分割三角形得出：四边形：1根，五边形：2根，六边形：3根，由类比推理可知，n边形：(n－3)根，如图所示．
(1)本题运用了数形结合思想，使问题更直观，易懂， 还运用了从特殊到一般的思想，由四边形、五边 形、六边形类比出n边形．此题为一道规律探究题， 通过观察图形，分析、归纳，发现其中的规律．(2)从特殊到一般是一种重要的数学思想方法，其特 点是通过对特殊现象的认识，利用归纳、类比、 猜想、探索发现一般的知识，如一般性的结论、 解决问题的方法等．
(绵阳)王师傅用4根木条钉成一个四边形木架，如图所示，要使这个木架不变形，他至少要再钉上几根木条？(　　)A．0根　 　B．1根C．2根 D．3根
如图所示，建高楼常需要用塔吊来吊建筑材料，而塔吊的上部是三角形结构，这是应用了三角形的哪个性质？答：____________．(填“稳定性”或“不稳定性”)