初中鲁教版 (五四制)1 对函数的再认识课文内容ppt课件

这是一份初中鲁教版 (五四制)1 对函数的再认识课文内容ppt课件，共21页。PPT课件主要包含了教学目标，交流发现，最高水位是多少，表示函数关系的方法，图像法，列表法，解析法，交流探究，≤t≤7，课堂练习等内容，欢迎下载使用。

1.复习并进一步认识函数的定义，能够表示简单变量之间的函数关系。2.了解表示函数的方法。
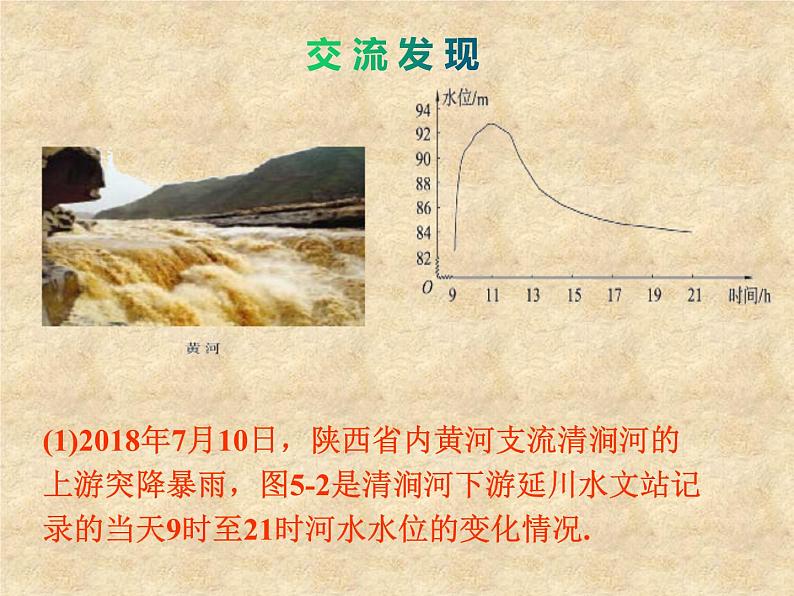
(1)2018年7月10日，陕西省内黄河支流清涧河的上游突降暴雨，图5-2是清涧河下游延川水文站记录的当天9时至21时河水水位的变化情况.
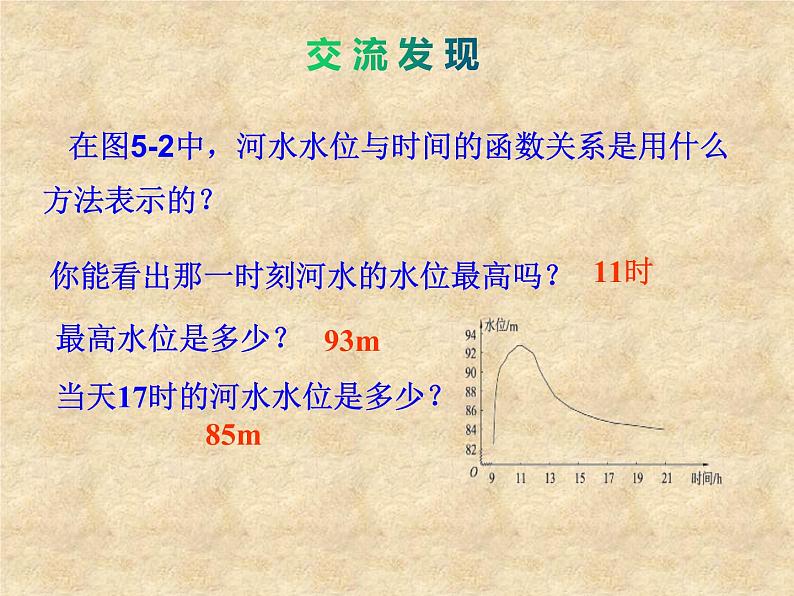
在图5-2中，河水水位与时间的函数关系是用什么方法表示的？
你能看出那一时刻河水的水位最高吗？
当天17时的河水水位是多少？
y与x之间的函数关系是用什么方法表示的？
（2）一根弹簧原长15cm，在弹性限度内，每增加10N的拉力，弹簧就伸长2cm，请你填写下表：
h与t之间的函数关系是用什么方法表示的？
当t=0(s)和t=1(s)时，对应的h值分别是多少？
（3）物体自由下落的高度h(m)与时间t(s) 之间的函数关系是h=4.9t2
（1）用数学式子表示函数的方法叫做解析法
（2）用表格表示函数关系的方法叫做列表法
（3）用图象表示函数关系的方法叫做图像法
用来表达函数关系的数学式子叫做函数解析式或函数关系式
上述的例子中，（1）（2）（3）分别是哪种表示函数的方法呢？
（1）是
你能试着举出用这三种方法表示函数的例子吗？
两个变量间的函数关系，可有不同的表示方法，上面的三方法在解决具体问题时，都有广泛的应用.
用描点法画函数图像时用到了函数关系的哪几种表示方法？
（1）在这个问题中，速度y与时间t之间的函数关系是用哪种方法表示的？
（2）时间t的取值范围是什么？
1.一辆汽车在行驶中，速度v随时间t变化的情况如图所示.
（3）当时间t为何值时，汽车行驶的速度最大？最大速度是多少？当时间t取何值时，速度为0？
（4）在哪一时间段汽车的行驶速度逐渐增加？在哪一时间段汽车的行驶速度逐渐减少？在那一时间段按匀速运动行驶?
例1 求下列函数中自变量x可以取值的范围:
例 一根蜡烛长20cm,每小时燃掉5cm.
(1)写出蜡烛剩余的长度y（cm）与燃烧时间x（h） 之间的函数解析式.
(2)求自变量x可以取值的范围;
(3)蜡烛点燃2h后还剩多长?
求下列函数中自变量x可以取值的范围:
等腰三角形ABC的周长为10cm,底边BC长为y(cm), 腰AB长为x（cm） (1)写出y与x之间的函数解析式;
(2)指出自变量x可以取值的范围.
油箱中有油300L,油从管道中匀速流出,1小时流完. 写出油箱中剩余的油量Q(L)与油流出时间t(s)之间 的函数解析式,并指出自变量t 可以取值的范围.
函数解析式:Q=300-5t
t的取值范围: 0≤t≤60
确定函数自变量可以取值的范围时,必须使函数解析式有意义.在解决实际问题时,还要使实际问题有意义.