2021学年1.3 集合的基本运算课堂教学ppt课件

这是一份2021学年1.3 集合的基本运算课堂教学ppt课件，共24页。PPT课件主要包含了所有元素，∁UA，不属于集合A，mm≥2，mm2等内容，欢迎下载使用。

[课程目标] 1.理解全集和补集的含义，会求给定子集的补集； 2.能够利用集合的补集的性质解决简单的参数问题．
知识点一　全集1．定义：如果一个集合含有所研究问题中涉及的___________， 那么就称这个集合为全集．2．记法：全集通常记作____．
【思辨】判断正误(请在括号中打“√”或“×”).(1)全集一定包括任何一个元素．(　　)(2)只有实数集R才可以作为全集．(　　)(3)为了研究集合A＝{1，2，3，4，5，6}，B＝{1，2，3}， C＝{1，3，5}之间的关系，要从中选一个集合作为全集， 这个集合是A.(　　)【解析】 (1)全集仅包含我们研究问题所涉及的全部元素，而非任何元素．(2)研究的问题并不一定是实数集，也有可能为整数集、自然数集或有理数集等．(3)根据全集的定义知应选集合A作为全集．
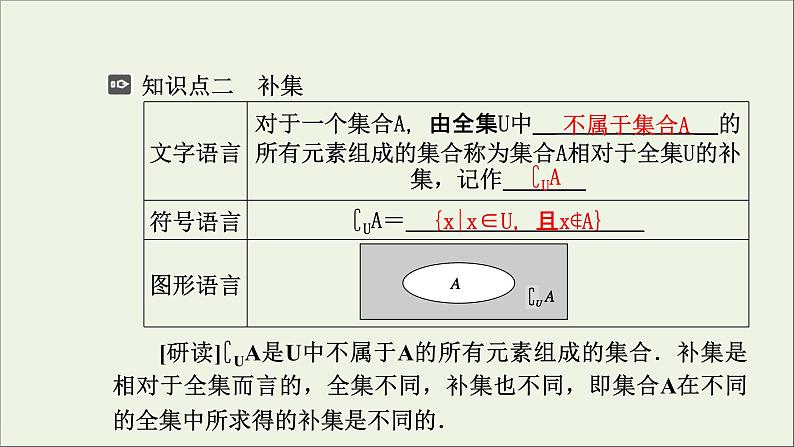
知识点二　补集 [研读]∁UA是U中不属于A的所有元素组成的集合．补集是相对于全集而言的，全集不同，补集也不同，即集合A在不同的全集中所求得的补集是不同的．
{x|x∈U，且x∉A}
【思辨】 判断正误(请在括号中打“√”或“×”).(1)一个集合的补集一定含有元素．(　　)(2)集合∁AC与集合∁BC相等．(　　)(3)(∁UA)∪A＝U.(　　)(4)(∁UA)∩A＝∅.(　　)(5)∁U∅＝U.(　　)【解析】 (1)因为全集的补集是空集，即∁UU＝∅，所以这个说法错误．(2)当A＝B时，二者相等，否则不相等．根据补集的定义知，(3)(4)(5)中等式成立．
例1 若全集M＝{－1，0，1，2，3}，N＝{x|x2＝1，x∈Z}，则∁MN等于(　　)A．∅　　　　　　　　B．{0，2，3}C．{－1，1} D．{0，1，2，3}【解析】 因为M＝{－1，0，1，2，3}，N＝{x|x2＝1，x∈Z}＝{－1，1}，根据补集的定义，得∁MN＝{0，2，3}．
已知全集U＝{a，b，c，d，e}，集合A＝{b，c，d}，B＝{c，e}，则(∁UA)∪B等于(　　)A．{b，c，e} B．{c，d，e}C．{a，c，e} D．{a，c，d，e}【解析】 由U＝{a，b，c，d，e}，A＝{b，c，d}，得∁UA＝{a，e}，又B＝{c，e}，所以(∁UA)∪B＝{a，c，e}．
解：A∩B＝{4}，A∪B＝{3，4，5，7，8}，又∁UA＝{1，2，6，7，8}，∁UB＝{1，2，3，5，6}，所以(∁UA)∩(∁UB)＝{1，2，6}，A∩(∁UB)＝{3，5}，(∁UA)∪B＝{1，2，4，6，7，8}． [规律方法] 解答此类问题的关键在于准确使用Venn图表示集合，并熟悉几种常见运算的对应图形，此外，还要熟悉集合的基本运算．
例3 若全集U＝{2，4，a2－a＋1}，A＝{a＋4，4}，∁UA＝{7}，则实数a＝________．【解析】 因为∁UA＝{7}，所以7∈U且7∉A，所以a2－a＋1＝7，解得a＝－2或a＝3.当a＝3时，A＝{4，7}，与7∉A矛盾，当a＝－2时满足题意，所以a＝－2.
设U＝{0，1，2，3}，A＝{x∈U|x2＋mx＝0}，若∁UA＝{1，2}，则实数m＝______．【解析】 因为U＝{0，1，2，3}，∁UA＝{1，2}，所以A＝{0，3}．所以0，3是方程x2＋mx＝0的两根，所以m＝－3.
例4 已知集合A＝{x|x>a2＋1或x已知集合A＝{x|x2－4mx＋2m＋6＝0，x∈R}，B＝{x|x<0，x∈R}，若A∩B≠∅，求实数m的取值范围．
[规律方法] 在求解含参的不等式和方程等问题时，如果问题的正面包含较多的情况，我们可以考虑补集的思想，定义一个全集，然后再从全集中求出问题的反面，进而通过取补集，使得原问题得解．
例5 设集合A＝{x|x＋m≥0}，B＝{x|－2【迁移探究1】 将本例条件“(∁UA)∩B＝∅”改为“(∁UA)∩B≠∅” 其他条件不变，则m的取值范围是____________．【解析】 由已知得A＝{x|x≥－m}，所以∁UA＝{x|x<－m}，又(∁UA)∩B≠∅，所以－m>－2，解得m<2.所以m的取值范围是{m|m<2}．【迁移探究2】 将本例条件“(∁UA)∩B＝∅”改为“(∁UB)∪A＝R” 其他条件不变，则m的取值范围是___________．【解析】 由已知得A＝{x|x≥－m}，∁UB＝{x|x≤－2或x≥4}.又(∁UB)∪A＝R，所以－m≤－2，解得m≥2.所以m的取值范围是{m|m≥2}．
[规律方法]由集合的补集求解参数的问题．(1)如果所给集合是有限集，由补集求参数问题时，可利用补集 定义并结合相关知识求解．(2)如果所给集合是无限集，与集合的交集、并集、补集运算有 关的求参数问题时，一般利用数轴分析法求解．
已知集合A＝{x|－2＜x＜3}，B＝{x|m＜x＜m＋9}，若(∁RA)∩B＝B，则实数m的取值范围是______________________．【解析】 ∁RA＝{x|x≤－2或x≥3}，由(∁RA)∩B＝B，得B⊆(∁RA)，∴m＋9≤－2或m≥3.故m的取值范围是{m|m≤－11或m≥3}.
{m|m≤－11或m≥3}
1．已知全集U＝R，集合A＝{x|1≤2x＋1<9}，则∁UA＝(　　)A． {x|x<0或x>4}　　B． {x|x≤0或x>4}C． {x|x≤0或x≥4} D．{x|x<0或x≥4}【解析】 因为U＝R，A＝{x|0≤x<4}，所以∁UA＝{x|x<0或x≥4}．
2．已知全集U＝M∪N＝{1，2，3，4，5}，M∩(∁UN)＝{2，4}，则N＝(　　)A．{1，2，3} B．{1，3，5}C．{1，4，5} D．{2，3，4}【解析】 因为M∩(∁UN)＝{2，4}，所以元素2，4是∁UN中的元素，即2，4一定不是N中的元素，故选项A，C，D错误．故选B. 
3．已知全集U＝{x|x≤5}，集合A＝{x|－3≤x<5}，则∁UA＝( 　)A．{x|x<－3或x＝5}B．{x|x<－3}C．{x|－34．已知全集U＝{2，5，8}，且∁UA＝{2}，则集合A的真子集有____个．【解析】 因为U＝{2，5，8}，∁UA＝{2}，所以A＝{5，8}，A的真子集为{5}，{8}，∅，共3个．5．设U＝R，A＝{x|a≤x≤b}，∁UA＝{x|x>4或x<3}，则a＋b＝____．【解析】 因为∁UA＝{x|x>4或x<3}，所以A＝{x|3≤x≤4}，所以a＝3，b＝4，所以a＋b＝7.