






人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质课堂教学ppt课件
展开[课程目标] 1.理解函数单调性的定义及其几何意义;明确增函 数、减函数的图象特征; 2.能根据图象写出函数的单调区间,并能利用定义 进行证明.
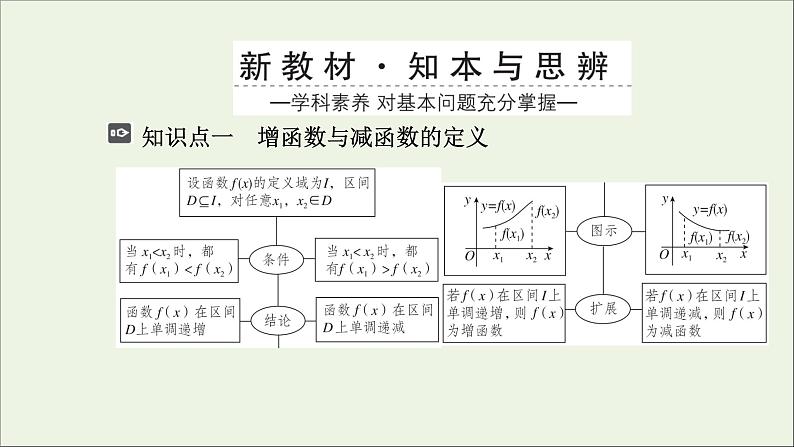
知识点一 增函数与减函数的定义
[研读]单调性是与“区间”紧密相关的概念,一个函数在定义域的不同区间上可以有不同的单调性,即单调性是函数的一个“局部”性质.
【思辨】 判断正误(请在括号中打“√”或“×”).(1)所有的函数在定义域上都具有单调性.( )(2)函数f(x)的定义域为D, 存在x1,x2∈D,若x1
知识点二 单调性与单调区间如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)__________,区间D叫做y=f(x)的______________.
【思辨】 判断正误(请在括号中打“√”或“×”).(1)函数的单调区间是函数定义域的子集.( )(2)函数f(x)=- 的单调递增区间是(-∞,0)∪(0,+∞).( )(3)函数f(x)=x2-2x(x∈[-1,2])的单调递增区间是[1,2],单 调递减区间是[-1,1].( )(4)函数y=2x+1在[0,3]上单调递增,则[0,3]是函数的单调 递增区间.( )
例1 画出函数y=x2-2|x|+2的图象,并讨论函数的单调性.
1.定义在区间[-5,5]上的函数y=f(x)的图象如图所示,则函数的单调递减区间是______________,___________,在区间__________,____________上单调递增.
2.作出函数f(x)=x2-|x|的图象,并讨论函数的单调性.
例2 (1)利用定义判断函数f(x)= 在区间(0,+∞)上的单调性;(2) 利用定义判断函数f(x)=x3在R上的单调性.
求证:函数f(x)=x+ (a>0)在区间(0,)上单调递减.
[规律方法]证明函数f(x)在区间D上的单调性应遵循以下步骤:①设元:设∀x1,x2∈D,且x1
已知函数f(x)在区间[-1,1]上单调递减,且f(1-a)>f(a2-1),则实数a的取值范围为__________.
[规律方法] 解决与抽象函数有关的变量的取值范围问题,关键是利用单调性“脱去”函数符号“f”,从而转化为熟悉的不等式.具体做法是:①若函数y=f(x)在区间D上单调递增,对任意x1,x2∈D,且f(x1)
例4 (1)若函数f(x)=-x2+2ax+1在区间(-∞,2)上单调递增,则实数a的取值范围是________________;【解析】 f(x)=-x2+2ax+1=-(x-a)2+1+a2,抛物线开口向下,当对称轴x=a≥2时,f(x)在区间(-∞,2)上单调递增,所以实数a的取值范围是[2,+∞).
[规律方法] 对于一次函数、二次函数基本初等函数的单调性问题中所涉及的参数问题,要根据这些函数的图象、性质进行讨论.
1.若函数f(x)=ax2-(a-1)x+5在区间 上单调递增, 求实数a的取值范围.
2.已知函数f(x)=x3-3x,x∈[-a,a],若f(x)在[-a,a]上单 调递减,求实数a的取值范围.
1.函数y=x2-6x的单调递减区间是( )A.(-∞,2]B.[2,+∞)C.[3,+∞)D.(-∞,3]【解析】 函数y=x2-6x的图象的对称轴为直线x=3,所以函数的单调递减区间是(-∞,3].
2.下列四个函数中,在区间(0,+∞)上单调递增的是( )
3.[0,3]是函数f(x)定义域内的一个区间,若f(1)
高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质多媒体教学ppt课件: 这是一份高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质多媒体教学ppt课件,共33页。PPT课件主要包含了fx0=M,纵坐标,答案D,答案4等内容,欢迎下载使用。
高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质教学演示ppt课件: 这是一份高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质教学演示ppt课件,共38页。PPT课件主要包含了预学案,共学案,fx0=M,纵坐标,答案C,答案A等内容,欢迎下载使用。
人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt: 这是一份人教A版 (2019)必修 第一册3.2 函数的基本性质教课课件ppt,共38页。PPT课件主要包含了预学案,共学案,单调递增,增函数,单调递减,减函数,答案B,单调递增或单调递减,单调性,单调区间等内容,欢迎下载使用。













