2022春华东师大版七年级数学下册第9章多边形9.1三角形9.1.4三角形的外角性质授课课件

这是一份2022春华东师大版七年级数学下册第9章多边形9.1三角形9.1.4三角形的外角性质授课课件，共31页。
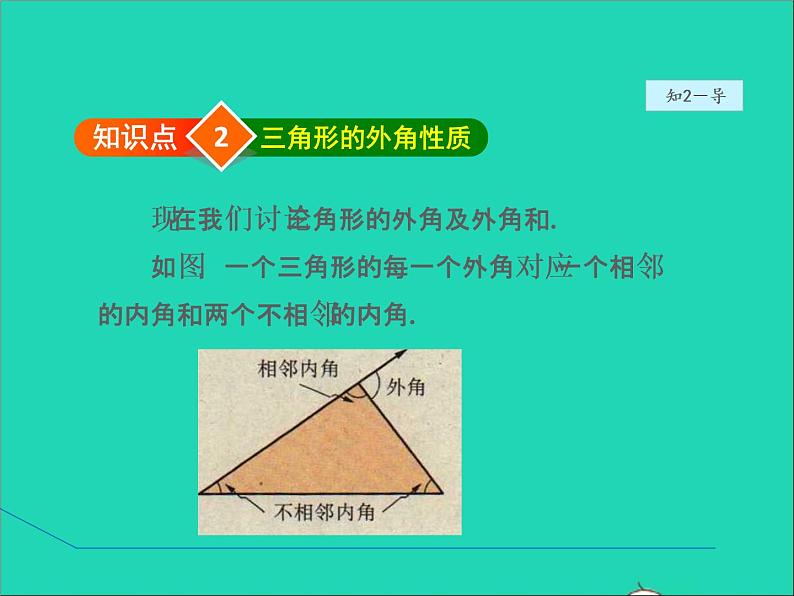
9.1 三角形第4课时 三角形的外 角性质第9章 多边形1课堂讲解三角形的外角定义三角形的外角性质三角形的外角和2课时流程逐点导讲练课堂小结作业提升 如图给我们展示了一个三角形的钢架，在实际生活中这样的例子很多，这主要是利用三角形的稳定性，除此之外，你还知道三角形的哪些性质呢?1知识点三角形的外角定义1. 三角形外角的定义 三角形的一个内角的一边与另一边的反向延长线所 组成的角叫做三角形的外角．知1－讲在△ABC中，∠A等于和它相邻的外角的四分之一，这个外角等于∠B的两倍，那么∠A＝_______，∠B＝_______，∠C＝_______.知1－讲例1 解析：∠A和与它相邻的外角互为邻补角，∠A又等于和它相邻的外角的四分之一，所以∠A＝36°，∠A的外角为144 °，所以∠B＝72°，根据三角形内角和为180°，可以求得∠C＝72°.36°72°72°知1－讲 三角形的外角与他相邻的内角互补.1下边的角是△ABC的外角的是( )A. ∠ACE B.∠ACF C. ∠BCD D.∠ACB如图，下列关于△ABC的外角的说法正确的是(　　)A．∠HBA是△ABC的外角B．∠HBG是△ABC的外角C．∠DCE是△ABC的外角D．∠GBA是△ABC的外角知1－练22知识点三角形的外角性质知2－导 现在我们讨论三角形的外角及外角和. 如图，一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角. 三角形的外角与内角有什么关系呢？ 在图中，显然有∠CBD(外角)+∠ABC(相邻的内角)=180°. 那么外角∠CBD与其他两个不相邻的内角又有什么关系呢？ 依据三角形的内角和等于180°，我们有∠ACB +∠BAC +∠ABC = 180°.知2－导 由上面两个式子，可以推出 ∠ CBD = 180°－∠ABC, ∠ACB + ∠BAC = 180°－∠ABC. 因而可以得到你与你的同伴所发现的结论： ∠CBD =∠ACB +∠BAC.知2－导由此可知，三角形的外角有两条性质：三角形的一个外角等于与它不相邻的两个内 角的和.三角形的一个外角大于任何一个与它不相邻 的内角.知2－导要点精析：(1)性质1反映了三角形的外角与不相邻内角的数量 关系，利用它可以求相关的角，可以证明一个 角等于另两个角的和与差，利用它作为中间关 系证明两个角相等. (2)性质2反映了三角形的外角与不相邻内角的大小 关系，利用它可以证明角的不等关系．知2－讲知2－讲如图，D是△ABC的BC于边上一点，∠B= ∠BAD， ∠ADC=80°， ∠BAC=70°. 求：(1)∠B的度数；(2)∠C的度数．例2(1)∵ ∠ADC是△ABD的外角(已知)， ∴∠B+ ∠BAD =∠ADC=80° (三角形的一个 外角等于与它不相邻的两个内角的和). 又∵∠B= ∠BAD(已知）， ∴∠B = 80°× = 40°(等量代换).(2) ∵∠B+ ∠BAC +∠C = 180°(三角形的内角 和等于180°)， ∴∠C = 180°－∠B－∠BAC(等式的性质） =180°－40°－70°=70°.知2－讲解：知2－讲 利用三角形的外角的性质求角的度数常与内角的度数相结合来应用.1如图，已知∠BAD＝∠CBE＝∠ACF，∠FDE＝48°，∠DEF＝64°，求△ABC各内角的度数．知2－练知2－练2若三角形的一个外角小于与它相邻的内角，则这个三角形是(　　)A．直角三角形 　　B．锐角三角形C．钝角三角形 　　D．钝角三角形或锐角三角形如图，∠A，∠1，∠2的大小关系是(　　)A．∠A＞∠1＞∠2 B．∠2＞∠1＞∠AC．∠A＞∠2＞∠1 D．∠2＞∠A＞∠13如图，请确定∠1与∠2的大小关系，并说明为什么？例3 导引：要判断∠1与∠2的大小关系，而这两个角间没有直接关系，则需找出一个角作为桥梁将这两个角联系起来，∠3能担当这种角色；用三角形外角的性质，先判断∠3与∠2的大小关系，再判断∠1与∠3的大小关系，用不等式的传递性判断∠1与∠2的大小关系．知2－讲解：∠1>∠2. 理由如下：∵∠1是△ABC的一个外角，∴∠1>∠3.∵∠3是△FGC的一个外角，∴∠3>∠2，∴∠1>∠2.知2－讲 “三角形的一个外角大于与它不相邻的任何一个内角”，是证明有关角的不等关系的一条重要性质，它常常结合不等式的传递性、不等式的性质来解决有关角的不等关系；用它可判断与三角形有关的角的大小问题．本题通过∠3把∠1和∠2联系在一起．知2－讲1(一题多解)如图，点D是△ABC内任意一点，试说明：∠BDC>∠A.知2－练2如图，在△ABC中，点D是∠ACB与∠ABC的平分线的交点，BD的延长线交AC于点E.(1)若∠A＝70°，求∠BDC的度数；(2)若∠EDC＝50°，求∠A的度数；(3)请直接写出∠A与∠BDC之间的数量关系(不必 说明理由)．知2－练3知识点三角形的外角和知3－导 与三角形的每个内角相邻的外角分别有两个，这两个外角是对顶角. 从与每个内角相邻的两个外角中分别取一个相加，得到的和称为三角形的外角和. 如图所示，∠1+∠2+∠3就是△ABC的外角和.知3－导在图中， ∠1+______=180°，∠2+______=180°，∠3+______=180°.三式相加可以得到∠1+∠2+∠3+______+______+______=______. ① 而∠ACB +∠BAC +∠ABC= 180°， ②将①与②相比较，你能得出什么结论?可以得到： ∠1+∠2+∠3= 360°.由此可知：三角形的外角和等于360°.知3－导三角形的外角和等于360°.要点精析： 三角形的外角和指的是三角形的每个顶点处各取一个外角相加所得到的和，而不是指六个外角的和．知3－讲如果三角形三个外角度数之比是3:4:5，则此三角形一定是( )A.锐角三角形 B.直角三角形C.钝角三角形 D.不能确定例4 分析：根据三角形外角和定理和三角形外角的性质解答.知3－讲解：∵三角形三个外角度数之比是3：4：5，设三个外角分别是α，β，γ，则α=360°× =90°，∴此三角形一定是直角三角形. 故选B．B 利用三角形的外角的性质求角的度数常与内角的度数相结合来应用.知3－讲知3－讲已知三角形的三个外角的度数比为2∶3∶4，则它的最大内角的度数为( ) A.90° B. 110°C.100° D. 120°例5 分析：设三个外角的度数分别为2k，3k，4k，根据三角形外角和定理，可知2k°+3k°+4k° =360°，得k=40°，所以最小的外角为2k =80°，故最大的内角为180°- 80°=100° . 故选C.C1下列对三角形的外角和叙述正确的是(　　)A．三角形的外角和等于180°B．三角形的外角和就是所有外角的和C．三角形的外角和等于所有外角和的一半D．以上都不对如图，∠1＋∠2＋∠3＋∠4＝________度．知3－练2三角形内角和定理的推论： 三角形的外角等于与它不相邻的两个内角的和，大于和它不相邻的任一内角．此推论的主要应用有：(1)已知外角与和它不相邻的两个内角中的任意一个可 求“另一个”．(2)利用推论可证一个角为另两个角的和．(3)利用三角形内角和定理作为中间关系式证明两个角 相等．(4)可以证明两角的不等关系．