

【解析版】江西省九江市2022学年七年级上期末数学试卷
展开
江西省九江市2022学年七年级上学期期末数学试卷
一、选择题
1.(3分)﹣3的相反数是()
A. B. ﹣3 C. D. 3
2.(3分)经专家估算,南海内的油气资源约合15000亿美元,用科学记数法表示数字15000是()
A. 15×103 B. 1.5×104 C. 1.5×103 D. 1.5×105
3.(3分)下列各组两项中,是同类项的是()
A. 3x2y,3xy2 B. abc,ac C. ﹣2xy,﹣3ab D. xy,﹣xy
4.(3分)骰子是一种特别的数字立方体(如图),它要求相对两面的点数之和总是7,下面四幅图中可以折成符合要求的骰子的是()
A. B. C. D.
5.(3分)下列运算正确的是()
A. x﹣3y=﹣2xy B. x2+x3=x5 C. 5x2﹣2x2=3x2 D. 2x2y﹣xy2=xy
6.(3分)下列方程的变形中正确的是()
A. 由x+5=6x﹣7得x﹣6x=7﹣5 B. 由﹣2(x﹣1)=3得﹣2x﹣2=3
C. 由得 D. 由得2x=﹣12
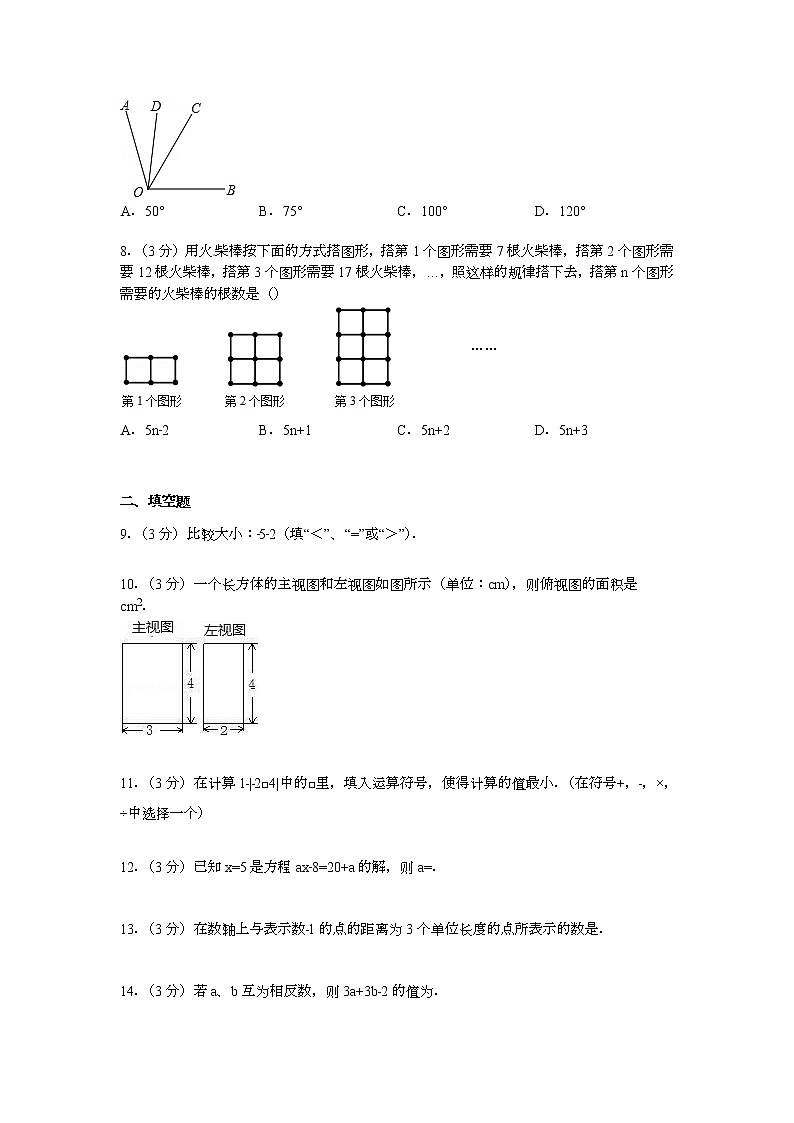
7.(3分)如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于()
A. 50° B. 75° C. 100° D. 120°
8.(3分)用火柴棒按下面的方式搭图形,搭第1个图形需要7根火柴棒,搭第2个图形需要12根火柴棒,搭第3个图形需要17根火柴棒,…,照这样的规律搭下去,搭第n个图形需要的火柴棒的根数是()
A. 5n﹣2 B. 5n+1 C. 5n+2 D. 5n+3
二、填空题
9.(3分)比较大小:﹣5﹣2(填“<”、“=”或“>”).
10.(3分)一个长方体的主视图和左视图如图所示(单位:cm),则俯视图的面积是cm2.
11.(3分)在计算1﹣|﹣2□4|中的□里,填入运算符号,使得计算的值最小.(在符号+,﹣,×,÷中选择一个)
12.(3分)已知x=5是方程ax﹣8=20+a的解,则a=.
13.(3分)在数轴上与表示数﹣1的点的距离为3个单位长度的点所表示的数是.
14.(3分)若a、b互为相反数,则3a+3b﹣2的值为.
15.(3分)若xny与x3ym﹣1是同类项,则mn=.
16.(3分)观察下列运算并填空:
32﹣12=8×1
52﹣32=8×2;
72﹣52=8×3;
…
根据以上等式发现规律,用代数式表示这个规律为.
三、计算
17.(5分)计算:﹣32+8×(﹣2)2﹣(﹣4)÷(﹣1)
18.(5分)先化简,再求值:2(a2b+3ab2)﹣3(a2b﹣1)﹣2a2b﹣2,其中a=﹣2,b=2.
19.(5分)解方程:.
四、解答题
20.(6分)如图,某小区规划在长为b,宽为a的长方形空地上建造三块公共设施(一个大半圆和两个小半圆),并在中间修一条等宽为n的小路,其他部分全部铺上草地,求草地面积?所得结果是一个几次几项式?
21.(6分)已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.
22.初中生的体育锻炼问题一直是教育工作者关注的问题之一,为此某现教育局对该县部分学校2022学年七年级学生的体育锻炼时间进行一次抽样调查(分为三个层级,A级:每天能坚持体育锻炼两个小时;B级:每天能参加体育锻炼一个小时;C级:每天很少进行体育锻炼),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了名学生.
(2)将图①补充完整
(3)求出图②中A级所占的圆心角的度数
(4)根据抽样调查结果,请你估计该县近6000名初中生大约有多少名学生参加体育锻炼时间达标(达标包括A级和B级)?
23.某电信公司按以下规定收取手机流量费:若每月流量不超过50MB,则流量按0.1元/MB收费;若超过50MB,则超过部分按0.2元/MB收费.如果某手机用户在某月的平均流量费为0.15元/MB,那么这个月他共用了多少流量?
24.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在O处,一直角边OM在射线O上,另一直角边ON在直线AB的下方
(1)将图1中的三角形绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC,问:此时直线ON是否平分∠AOC?计算出图中相关角的度数说明你的观点;
(2)将图1中的三角板以每秒10°的速度绕点O逆时针方向旋转一周,在旋转过程中,第n秒时,直线ON恰好平分∠AOC,则n的值为(直接写出答案);
(3)将图1中三角板绕点O旋转至图3,使ON在∠AOC的内部时,求∠AOM﹣∠NOC的度数.
江西省九江市2022学年七年级上学期期末数学试卷
参考答案与试题解析
一、选择题
1.(3分)﹣3的相反数是()
A. B. ﹣3 C. D. 3
考点: 相反数.
分析: 根据只有符号不同的两个数互为相反数,可得答案.
解答: 解:﹣3的相反数是3,
故选:D.
点评: 本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.
2.(3分)经专家估算,南海内的油气资源约合15000亿美元,用科学记数法表示数字15000是()
A. 15×103 B. 1.5×104 C. 1.5×103 D. 1.5×105
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:15000=1.5×104,
故选:B.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(3分)下列各组两项中,是同类项的是()
A. 3x2y,3xy2 B. abc,ac C. ﹣2xy,﹣3ab D. xy,﹣xy
考点: 同类项.
分析: 本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,几个常数项也是同类项.同类项与字母的顺序无关,与系数无关.
解答: 解:A、相同字母的指数不相同,不是同类项;
B、所含字母不相同,不是同类项;
C、所含字母不相同,不是同类项;
D、符合同类项的定义,是同类项.
故选D.
点评: 同类项定义中的两个“相同”:
(1)所含字母相同;
(2)相同字母的指数相同,是易混点;
同类项定义中隐含的两个“无关”:
①与字母的顺序无关;②与系数无关.
本题还应注意同类项是针对整式而言的.
4.(3分)骰子是一种特别的数字立方体(如图),它要求相对两面的点数之和总是7,下面四幅图中可以折成符合要求的骰子的是()
A. B. C. D.
考点: 展开图折叠成几何体;专题:正方体相对两个面上的文字.
分析: 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点对各选项分析判断后利用排除法求解.
解答: 解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点与3点是相对面,4点与6点是相对面,2点与5点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
B、3点与4点是相对面,1点与5点是相对面,2点与6点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
C、4点与3点是相对面,5点与2点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项正确;
D、1点与5点是相对面,3点与4点是相对面,2点与6点是相对面,所以不可以折成符合规则的骰子,故本选项错误.
故选C.
点评: 本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
5.(3分)下列运算正确的是()
A. x﹣3y=﹣2xy B. x2+x3=x5 C. 5x2﹣2x2=3x2 D. 2x2y﹣xy2=xy
考点: 合并同类项.
分析: 依据同类项的定义以及合并同类项的法则即可作出判断.
解答: 解:A、不是同类项,不能合并,选项错误;
B、不是同类项,不能合并,选项错误;
C、正确;
D、不是同类项,不能合并,选项错误.
故选C.
点评: 本题考查了合并同类项的法则,正确理解同类项的定义是关键.
6.(3分)下列方程的变形中正确的是()
A. 由x+5=6x﹣7得x﹣6x=7﹣5 B. 由﹣2(x﹣1)=3得﹣2x﹣2=3
C. 由得 D. 由得2x=﹣12
考点: 解一元一次方程.
分析: 分别对所给的四个方程利用等式性质进行变形,可以找出正确答案.
解答: 解:A、由x+5=6x﹣7得x﹣6x=﹣7﹣5,故错误;
B、由﹣2(x﹣1)=3得﹣2x+2=3,故错误;
C、由得=1,故错误;
D、正确.
故选D.
点评: 本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.
7.(3分)如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于()
A. 50° B. 75° C. 100° D. 120°
考点: 角的计算;角平分线的定义.
专题: 计算题.
分析: 根据角的平分线定义得出∠AOD=∠COD,∠AOB=2∠AOC=2∠BOC,求出∠AOD、∠AOC的度数,即可求出答案.
解答: 解:∵OC是∠AOB的平分线,OD是∠AOC的平分线,∠COD=25°,
∴∠AOD=∠COD=25°,∠AOB=2∠AOC,
∴∠AOB=2∠AOC=2(∠AOD+∠COD)=2×(25°+25°)=100°,
故选:C.
点评: 本题考查了对角平分线定义和角的计算等知识点的应用,主要考查学生运用角平分线定义进行推理的能力和计算能力,题目较好,难度不大.
8.(3分)用火柴棒按下面的方式搭图形,搭第1个图形需要7根火柴棒,搭第2个图形需要12根火柴棒,搭第3个图形需要17根火柴棒,…,照这样的规律搭下去,搭第n个图形需要的火柴棒的根数是()
A. 5n﹣2 B. 5n+1 C. 5n+2 D. 5n+3
考点: 规律型:图形的变化类.
专题: 规律型.
分析: 观察不难发现,后一个图形比前一个图形多5根火柴棒,根据此规律写出第n个图形的火柴棒的根数即可.
解答: 解:∵搭第1个图形需要7根火柴棒,7=5+2,
搭第2个图形需要12根火柴棒,12=5×2+2,
搭第3个图形需要17根火柴棒,17=5×3+2,
…,
∴搭第n个图形需要的火柴棒的根数是5n+2.
故选C.
点评: 本题是对图形变化规律的考查,仔细观察图形得到后一个图形比前一个图形多5根火柴棒是解题的关键.
二、填空题
9.(3分)比较大小:﹣5<﹣2(填“<”、“=”或“>”).
考点: 有理数大小比较.
专题: 探究型.
分析: 根据两负数比较大小的法则进行比较即可.
解答: 解:∵|﹣5|=5>|﹣2|=2,
∴﹣5<﹣2.
故答案为:<.
点评: 本题考查的是有理数的大小比较,熟知两个负数,绝对值大的其值反而小是解答此题的关键.
10.(3分)一个长方体的主视图和左视图如图所示(单位:cm),则俯视图的面积是6cm2.
考点: 由三视图判断几何体.
分析: 根据给出的长方体的主视图和左视图可得,俯视图的长方形的长与主视图的长方形的宽相等为3,俯视图的长方形的宽与左视图的长方形的宽相等为2.因此俯视图的面积是6cm2.
解答: 解:俯视图是边长分别为3和2的长方形,因而其面积为6cm2.
点评: 考查立体图形的三视图和学生的空间想象能力.
11.(3分)在计算1﹣|﹣2□4|中的□里,填入运算符号×,使得计算的值最小.(在符号+,﹣,×,÷中选择一个)
考点: 有理数的混合运算;有理数大小比较.
分析: 将运算符号代入计算,比较大小即可.
解答: 解:根据题意得:1﹣|﹣2+4|=1﹣2=﹣1;1﹣|﹣2﹣4|=1﹣6=﹣5;1﹣|﹣2×4|=1﹣8=﹣7;1﹣|﹣2÷4|=,
则要使算式的值最小,这个符号是×.
故答案为:×.
点评: 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
12.(3分)已知x=5是方程ax﹣8=20+a的解,则a=7.
考点: 方程的解.
专题: 计算题.
分析: 使方程左右两边相等的未知数的值是该方程的解.将方程的解代入方程可得关于a的一元一次方程,从而可求出a的值.
解答: 解:把x=5代入方程ax﹣8=20+a
得:5a﹣8=20+a,
解得:a=7.
故答案为:7.
点评: 已知条件中涉及到方程的解,可以把方程的解代入原方程,转化为关于字母a的方程进行求解.
13.(3分)在数轴上与表示数﹣1的点的距离为3个单位长度的点所表示的数是﹣4或2.
考点: 数轴.
专题: 数形结合.
分析: 此题可借助数轴用数形结合的方法求解.由于点与﹣1的距离为3,那么应有两个点,记为A1,A2,分别位于﹣1两侧,且到﹣1的距离为3,这两个点对应的数分别是﹣1﹣3和﹣1+3,在数轴上画出A1,A2点如图所示.
解答: 解:因为点与﹣1的距离为3,
所以这两个点对应的数分别是﹣1﹣3和﹣1+3,
即为﹣4或2.
故答案为﹣4或2.
点评: 此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.
14.(3分)若a、b互为相反数,则3a+3b﹣2的值为﹣2.
考点: 代数式求值;相反数.
专题: 计算题.
分析: 根据相反数的定义得到a+b=0,再变形3a+3b﹣2得到3(a+b)﹣2,然后把a+b=0整体代入计算即可.
解答: 解:∵a、b互为相反数,
∴a+b=0,
∴3a+3b﹣2=3(a+b)﹣2=3×0﹣2=﹣2.
故答案为﹣2.
点评: 本题考查了代数式求值:先把所求的代数式根据已知条件进行变形,然后利用整体思想进行计算.也考查了相反数.
15.(3分)若xny与x3ym﹣1是同类项,则mn=8.
考点: 同类项.
分析: 根据同类项的概念求解.
解答: 解:∵xny与x3ym﹣1是同类项,
∴n=3,m﹣1=1,
∴m=2,n=3.
则mn=8.
故答案为:8.
点评: 本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.
16.(3分)观察下列运算并填空:
32﹣12=8×1
52﹣32=8×2;
72﹣52=8×3;
…
根据以上等式发现规律,用代数式表示这个规律为(2n+1)2﹣(2n﹣1)2=8n.
考点: 规律型:数字的变化类.
分析: 等式的左边是两个连续奇数的平方差,右边是这两个连续奇数的和除以4的商的8倍.
解答: 解:∵32﹣12═8×1=8×,
52﹣32=8×2=8×,
72﹣52=8×3=8×,
…
∴设n(n≥1)表示自然数,用关于n的等式表示这个规律为:(2n+1)2﹣(2n﹣1)2=8×=8n,
即(2n+1)2﹣(2n﹣1)2=8n.
故答案为:(2n+1)2﹣(2n﹣1)2=8n.
点评: 本题考查了规律型:数字的变化类,观察等式的规律时,既要分别观察等式的左边和右边,还要注意两边之间的联系.
三、计算
17.(5分)计算:﹣32+8×(﹣2)2﹣(﹣4)÷(﹣1)
考点: 有理数的混合运算.
分析: 先算乘方,和除法,再算乘法,最后算加减,由此顺序计算即可.
解答: 解:原式=﹣9+8×4﹣4×
=﹣9+32﹣3
=20.
点评: 此题考查有理数的混合运算,掌握运算顺序,正确判定运算符号计算即可.
18.(5分)先化简,再求值:2(a2b+3ab2)﹣3(a2b﹣1)﹣2a2b﹣2,其中a=﹣2,b=2.
考点: 整式的混合运算—化简求值.
分析: 根据去括号法则去掉括号,再合并同类项,然后代入数据计算即可.
解答: 解:2(a2b+3ab2)﹣3(a2b﹣1)﹣2a2b﹣2,
=2a2b+6ab2﹣3a2b+3﹣2a2b﹣2,
=﹣3a2b+6ab2+1,
当a=﹣2,b=2时,
原式=﹣3×(﹣2)2×2+6×(﹣2)×22+1=﹣71.
点评: 本题主要考查单项式乘多项式的运算法则以及合并同类项的法则,注意运算顺序以及符号的处理.
19.(5分)解方程:.
考点: 解一元一次方程.
专题: 计算题.
分析: 方程去分母,去括号,移项合并,将x系数化为1,即可求出解.
解答: 解:去分母得:5(x﹣1)=20﹣2(x+2),
去括号得:5x﹣5=20﹣2x﹣4,
移项合并得:7x=21,
解得:x=3.
点评: 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.
四、解答题
20.(6分)如图,某小区规划在长为b,宽为a的长方形空地上建造三块公共设施(一个大半圆和两个小半圆),并在中间修一条等宽为n的小路,其他部分全部铺上草地,求草地面积?所得结果是一个几次几项式?
考点: 列代数式;多项式.
分析: 由长为b,宽为a的长方形的面积减去底为n,高为a的平行四边形的面积,减去直径为a半圆的面积,再减去直径为a圆的面积,由此列式即可.
解答: 解:草地的面积为:ab﹣an﹣π(a)2﹣π(a)2
=ab﹣an﹣πa2,
是二次三项式.
点评: 此题考查列代数式,利用基本图形面积的和与差解决问题.
21.(6分)已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.
考点: 两点间的距离.
分析: 根据线段的和差,可得BC的长,根据线段的和差,可得(AB+CD)的长,根据线段中点的性质,可得(AE+DF)的长,再根据线段的和差,可得EF的长.
解答: 解:由线段的和差,得
AC+BD=AC+BC+CD=AD+BC=7+4=11cm,
由AD=10cm,得10+BC=11,
解得BC=1cm;
由线段的和差,得
AB+CD=AD﹣BC=10﹣1=9cm,
由E,F分别是线段AB,CD的中点,得
AE=AB,DF=CD,
由线段得和差,得
EF=AD﹣(AE+DF)=AD﹣(AB+CD)=10﹣(AB+CD)=10﹣=cm.
点评: 本题考查了两点间的距离,利用线段的和差得出(AB+CD)的长,再利用线段中点的性质得出(AB+CD)的长.
22.初中生的体育锻炼问题一直是教育工作者关注的问题之一,为此某现教育局对该县部分学校2014-2015学年七年级学生的体育锻炼时间进行一次抽样调查(分为三个层级,A级:每天能坚持体育锻炼两个小时;B级:每天能参加体育锻炼一个小时;C级:每天很少进行体育锻炼),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了200名学生.
(2)将图①补充完整
(3)求出图②中A级所占的圆心角的度数
(4)根据抽样调查结果,请你估计该县近6000名初中生大约有多少名学生参加体育锻炼时间达标(达标包括A级和B级)?
考点: 条形统计图;用样本估计总体;扇形统计图.
分析: (1)根据C级有50人,所占的百分比是25%,据此即可求得总人数;
(2)利用(1)中的结果减去其它各级别的人数即可求得A级的人数;
(3)利用360°乘以对应的比例即可;
(4)利用总人数6000乘以对应的比例.
解答: 解:(1)调查的总人数是:50÷25%=200(人),
故答案是:200;
(2)A级的人数是:200﹣120﹣50=30(人);
(3)A级所占的圆心角的度数是:360×=54°;
(4)参加体育锻炼时间达标的人数是:6000×=4500(人).
答:参加体育锻炼时间达标的人数是4500人.
点评: 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
23.某电信公司按以下规定收取手机流量费:若每月流量不超过50MB,则流量按0.1元/MB收费;若超过50MB,则超过部分按0.2元/MB收费.如果某手机用户在某月的平均流量费为0.15元/MB,那么这个月他共用了多少流量?
考点: 一元一次方程的应用.
分析: 首先设这个月他共用了xMB流量,由题意得等量关系:前50MB的费用+超过50MB的费用=0.15×总流量,根据等量关系列出方程,再解即可.
解答: 解:设这个月他共用了xMB流量,由题意得:
50×0.1+0.2(x﹣50)=0.15x,
解得:x=100.
答:这个月他共用了100MB流量.
点评: 此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中等量关系,列出方程.
24.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在O处,一直角边OM在射线O上,另一直角边ON在直线AB的下方
(1)将图1中的三角形绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC,问:此时直线ON是否平分∠AOC?计算出图中相关角的度数说明你的观点;
(2)将图1中的三角板以每秒10°的速度绕点O逆时针方向旋转一周,在旋转过程中,第n秒时,直线ON恰好平分∠AOC,则n的值为6或24(直接写出答案);
(3)将图1中三角板绕点O旋转至图3,使ON在∠AOC的内部时,求∠AOM﹣∠NOC的度数.
考点: 角的计算;余角和补角.
分析: (1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AOC=60°,则∠BON=30°,即旋转60°或240°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
解答: 解:(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,
即直线ON平分∠AOC;
(2)∵∠BOC=120°
∴∠AOC=60°,
∴∠BON=∠COD=30°,
即旋转60°时ON平分∠AOC,
由题意得,10n=60°或240°,
∴n=6或24;
故答案为:6或24;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
点评: 本题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
2022-2023学年江西省九江市七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年江西省九江市七年级(下)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江西省九江市七年级(下)期末数学试卷-(含解析): 这是一份2022-2023学年江西省九江市七年级(下)期末数学试卷-(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年江西省九江市七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年江西省九江市七年级(下)期末数学试卷(Word解析版),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












