【解析版】洛阳市宜阳县2022年八年级下期末数学试卷

这是一份【解析版】洛阳市宜阳县2022年八年级下期末数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
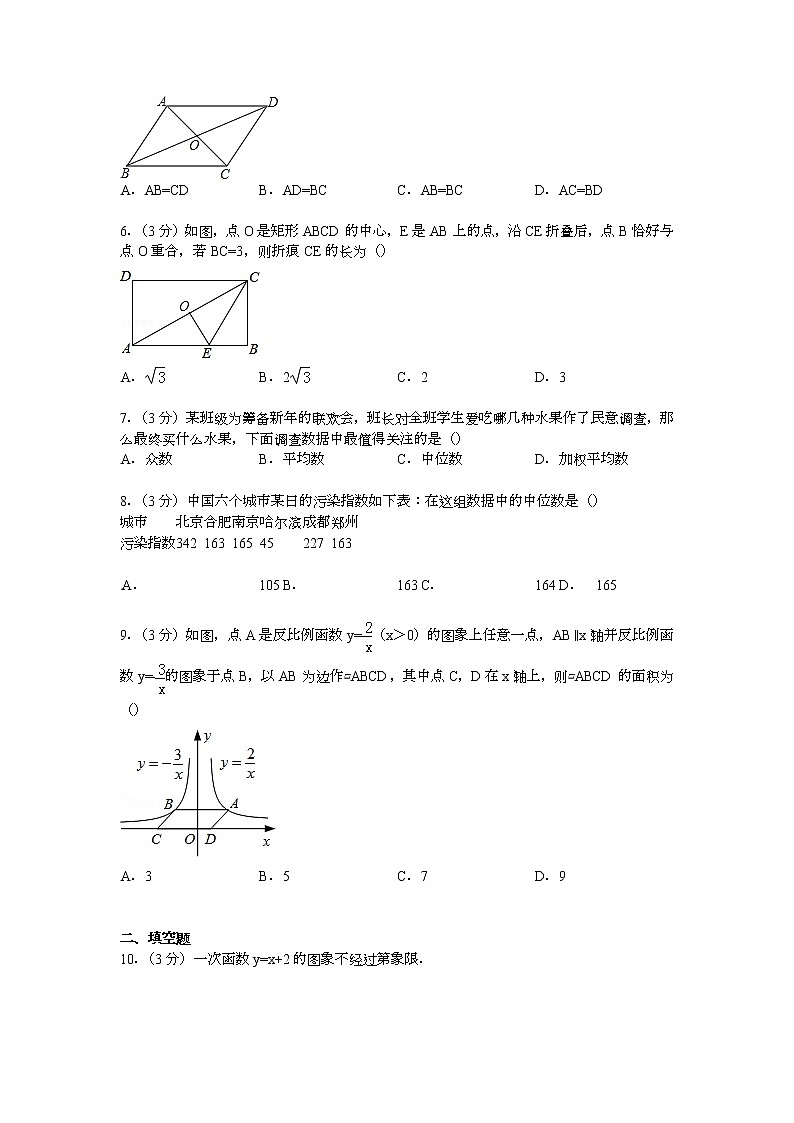
 河南省洛阳市宜阳县2022学年八年级下学期期末数学试卷 一、选择题1．（3分）下列分式中，为最简分式的是（） A．  B．  C．  D．  2．（3分）一次函数y=kx+k（k＜0）的图象大致是（） A．  B．  C．  D．  3．（3分）如图，矩形ABCD中，BE、CF分别平分∠ABC和∠DCB，点E、F都在AD上，下列结论不正确的是（ A． △ABE≌△DCF B． △ABE和△DCF都是等腰直角三角形 C． 四边形BCFE是等腰梯形 D． E、F是AD的三等分点 4．（3分）如图，点P是菱形ABCD内一点，PE⊥AB，PF⊥AD，垂足分别是E和F，若PE=PF，下列说法不正确的是（） A． 点P一定在菱形ABCD的对角线AC上 B． 可用H•L证明Rt△AEP≌Rt△AFP C． AP平分∠BAD D． 点P一定是菱形ABCD的两条对角线的交点 5．（3分）如图，下列条件中，能使▱ABCD成为菱形的是（） A． AB=CD B． AD=BC C． AB=BC D． AC=BD 6．（3分）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（） A．  B． 2 C． 2 D． 3 7．（3分）某班级为筹备新年的联欢会，班长对全班学生爱吃哪几种水果作了民意调查，那么最终买什么水果，下面调查数据中最值得关注的是（） A． 众数 B． 平均数 C． 中位数 D． 加权平均数 8．（3分）中国六个城市某日的污染指数如下表：在这组数据中的中位数是（） 城市 北京 合肥 南京 哈尔滨 成都 郑州污染指数 342 163 165 45 227 163  A． 105 B． 163 C． 164 D． 165 9．（3分）如图，点A是反比例函数y=（x＞0）的图象上任意一点，AB∥x轴并反比例函数y=﹣的图象于点B，以AB为边作▱ABCD，其中点C，D在x轴上，则▱ABCD的面积为（） A． 3 B． 5 C． 7 D． 9  二、填空题10．（3分）一次函数y=x+2的图象不经过第象限． 11．（3分）如果关于x的方程=无解，则m=． 12．（3分）如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别为2和3，则正方形的边长是． 13．（3分）菱形的两对条角线长分别为10cm、24cm，则它的周长为cm． 14．（3分）某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是分． 15．（3分）如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于点P．若四边形ABCD的面积是4，则DP的长是．  三、解答题16．（10分）计算（1）|﹣1|﹣（π﹣3）0+（）﹣1（2）﹣． 17．（8分）已知一个一次函数的图象与一个反比例函数的图象交于点P（﹣2，1）、Q（1，m）．（1）分别求出这两个函数的表达式．（2）在同一平面直角坐标系中画出这两个函数的图象，根据图象回答，当x取何值时，一次函数的值大于反比例函数的值？ 18．（9分）如图，在▱ABCD中，点E为CD的中点，连接BE并延长交AD的延长线于点F．求证：点E是BF的中点，点D是AF的中点． 19．（8分）如图，在矩形ABCD中，对角线AC与BD相交于点O，AE垂直且平分线段BO，垂足为点E，BD=15cm，求AC、AB的长． 20．（9分）如图，在△ABC中，AB=AC，点D是BC的中点，DE⊥AC于点E，DG⊥AB于点G，EK⊥AB于点K，GH⊥AC于点H、EK和GH相交于点F．求证：GE与FD互相垂直平分． 21．（9分）如图，在正方形ABCD中，CE⊥DF，求证：CE=DF． 22．（10分）某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：加工件数 540 450 300 240 210 120人数 1 1 2 6 3 2（1）写出这15人该月加工零件数的平均数、中位数和众数．（2）假如生产部负责人把每位工人的月加工零件数定为260（件），你认为这个定额是否合理，为什么？ 23．（12分）已知：如图，在△ABC中，D是BC边上的一点，连接AD，取AD的中点E，过点A作BC的平行线与CE的延长线交于点F，连接DF．（1）求证：AF=DC；（2）若AD=CF，试判断四边形AFDC是什么样的四边形？并证明你的结论．   河南省洛阳市宜阳县2022学年八年级下学期期末数学试卷参考答案与试题解析 一、选择题1．（3分）下列分式中，为最简分式的是（） A．  B．  C．  D．  考点： 最简分式． 分析： 最简分式的标准是分子，分母中不含有公因式，不能再约分．判断的方法是把分子、分母分解因式，并且观察有无互为相反数的因式，这样的因式可以通过符号变化化为相同的因式从而进行约分．解答： 解：A、的分子、分母都不能再分解，且不能约分，是最简分式；B、=；C、=；D、=；故选A．点评： 本题考查了最简分式的定义及求法．一个分式的分子与分母没有公因式时，叫最简分式．分式的化简过程，首先要把分子分母分解因式，互为相反数的因式是比较易忽视的问题．在解题中一定要引起注意． 2．（3分）一次函数y=kx+k（k＜0）的图象大致是（） A．  B．  C．  D．  考点： 一次函数的图象． 分析： 根据k＜0，由一次函数的性质即可判断出函数y=kx+k（k＜0）的图象所经过的象限．解答： 解：∵一次函数y=kx+k（k＜0），∴函数的图象经过二、三、四象限，故选D．点评： 本题考查的是一次函数的性质及一次函数图象与系数的关系：①k＞0，b＞0⇔y=kx+b的图象在一、二、三象限；②k＞0，b＜0⇔y=kx+b的图象在一、三、四象限； 3．（3分）如图，矩形ABCD中，BE、CF分别平分∠ABC和∠DCB，点E、F都在AD上，下列结论不正确的是（ A． △ABE≌△DCF B． △ABE和△DCF都是等腰直角三角形 C． 四边形BCFE是等腰梯形 D． E、F是AD的三等分点 考点： 矩形的性质． 分析： A、由AAS证得△ABE≌△DCF；B、根据矩形的性质、角平分线的性质推知△ABE和△DCF都是等腰直角三角形；C、由A中的全等三角形的性质得到BE=CF．结合矩形的对边平行得到四边形BCFE是等腰梯形；D、根据A在全等三角形的性质只能得到AE=DF，点E、F不一定是AD的三等分点．解答： 解：如图，∵四边形ABCD是矩形ABCD，∴∠A=∠D=∠DCB=∠ABC=90°．又BE、CF分别平分∠ABC和∠DCB，∴∠ABE=∠DCF=45°，∴∠AEB=∠ABE=45°，∠DFC=∠DCF=45°，∴AB=AE，DF=DC，∴△ABE和△DCF都是等腰直角三角形．故B正确； 在△ABE与△DCF中，．则△ABE≌△DCF（AAS），故A正确； ∵△ABE≌△DCF，∴BE=CF．又BE与FC不平行，且EF∥BC，EF≠BC，∴四边形BCFE是等腰梯形．故C正确； ∵△ABE≌△DCF，∴AE=DF．但是不能确定AE=EF=FD成立．即点E、F不一定是AD的三等分点．故D错误．故选：D．点评： 本题考查了矩形的性质，全等三角形的性质和判定，平行线的性质的应用，主要考查学生的推理能力． 4．（3分）如图，点P是菱形ABCD内一点，PE⊥AB，PF⊥AD，垂足分别是E和F，若PE=PF，下列说法不正确的是（） A． 点P一定在菱形ABCD的对角线AC上 B． 可用H•L证明Rt△AEP≌Rt△AFP C． AP平分∠BAD D． 点P一定是菱形ABCD的两条对角线的交点 考点： 菱形的性质；全等三角形的判定；角平分线的性质． 分析： 根据到角的两边距离相等的点在角的平分线上判断出AP平分∠BAD，根据菱形的对角线平分一组对角线可得AC平分∠BAD，然后对各选项分析判断利用排除法求解．解答： 解：∵PE⊥AB，PF⊥AD，PE=PF，∴AP平分∠BAD，∵四边形ABCD是菱形，∴对角线AC平分∠BAD，故A、C选项结论正确；可以利用“HL”证明Rt△AEP≌Rt△AFP，故B选项正确；点P在AC上，但不一定在BD上，所以，点P一定是菱形ABCD的两条对角线的交点不一定正确．故选D．点评： 本题考查了菱形的性质，到角的两边距离相等的点在角的平分线上的性质，全等三角形的判定与性质，熟练掌握各性质是解题的关键． 5．（3分）如图，下列条件中，能使▱ABCD成为菱形的是（） A． AB=CD B． AD=BC C． AB=BC D． AC=BD 考点： 菱形的判定． 分析： 根据菱形的性质逐个进行证明，再进行判断即可．解答： 解：A、▱ABCD中，本来就有AB=CD；故本选项错误；B、▱ABCD中本来就有AD=CB；故本选项错误；C、▱ABCD中，AB=BC，可利用邻边相等的平行四边形是菱形判定▱ABCD是菱形；故本选项正确；D、▱ABCD中，AC=BD，根据对角线相等的平行四边形是矩形，即可判定▱ABCD是矩形，而不能判定▱ABCD是菱形；故本选项错误．故选C．点评： 本题考查了平行四边形的性质，菱形的判定的应用，注意：菱形的判定定理有：①有一组邻边相等的平行四边形是菱形，②四条边都相等的四边形是菱形，③对角线互相垂直的平行四边形是菱形． 6．（3分）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（） A．  B． 2 C． 2 D． 3 考点： 翻折变换（折叠问题）． 分析： 由折叠的性质得出△CBE≌△COE，再由全等三角形的性质得出∠B=∠COE=90° CO=CB，∠BCE=∠ACE，证出OE是AC的垂直平分线，由线段垂直平分线的性质得出CE=AE，由等边对等角得出∠ACE=∠CAE，因此∠BCE=∠ACE=∠CAE，由直角三角形的性质得出∠BCE=30°，然后解直角三角形求出折痕CE的长即可．解答： 解：由折叠的性质得：△CBE≌△COE，∴∠B=∠COE=90°，CO=CB=3，∠BCE=∠ACE，∵O是矩形ABCD中心，∴CO=AO，∴OE垂直平分AC，∴CE=AE，∴∠ACE=∠CAE，∴∠BCE=∠ACE=∠CAE，在Rt△BCE中，∠BCE=30°，∵BC=3，∴CE==2；故选：B．点评： 本题考查了翻折变换的性质、矩形的性质、线段垂直平分线的判定与性质、等腰三角形的性质；熟练掌握翻折变换和矩形的性质，并能进行推理计算是解决问题的关键． 7．（3分）某班级为筹备新年的联欢会，班长对全班学生爱吃哪几种水果作了民意调查，那么最终买什么水果，下面调查数据中最值得关注的是（） A． 众数 B． 平均数 C． 中位数 D． 加权平均数 考点： 统计量的选择． 分析： 班长最值得关注的应该是哪种水果爱吃的人数最多，即众数．解答： 解：由于众数是数据中出现次数最多的数，故班长最值得关注的应该是统计调查数据的众数．故选A．点评： 此题主要考查统计的有关知识，主要包括平均数、中位数、众数的意义．反映数据集中程度的统计量有平均数、中位数、众数等，各有局限性，因此要对统计量进行合理的选择和恰当的运用． 8．（3分）中国六个城市某日的污染指数如下表：在这组数据中的中位数是（） 城市 北京 合肥 南京 哈尔滨 成都 郑州污染指数 342 163 165 45 227 163  A． 105 B． 163 C． 164 D． 165 考点： 中位数． 分析： 先把这组数据按照从小到大的顺序排列，然后根据中位数的概念求解．解答： 解：这组数据按照从小到大的顺序排列为：45，163，163，165，227，342，则中位数为：=164．故选C．点评： 本题考查了中位数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数． 9．（3分）如图，点A是反比例函数y=（x＞0）的图象上任意一点，AB∥x轴并反比例函数y=﹣的图象于点B，以AB为边作▱ABCD，其中点C，D在x轴上，则▱ABCD的面积为（） A． 3 B． 5 C． 7 D． 9 考点： 反比例函数系数k的几何意义． 专题： 计算题．分析： 连结OA、OB，如图，AB交y轴于E，根据反比例函数k的几何意义得到S△OAE=1，S△OBE=，则S△OAB=，然后根据平行四边形的面积公式求解．解答： 解：连结OA、OB，如图，AB交y轴于E，∵AB∥x轴，∴S△OAE=×|2|=1，S△OBE=×|﹣3|=，∴S△OAB=，∵四边形ABCD为平行四边形，∴▱ABCD的面积=2S△OAB=5．故选B．点评： 本题考查了反比例函数系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变． 二、填空题10．（3分）一次函数y=x+2的图象不经过第四象限． 考点： 一次函数的性质． 分析： 根据一次函数的性质可得出答案．解答： 解：∵1＞0，2＞0，∴一次函数的图象经过一、二、三象限，即不经过第四象限．故答案为：四．点评： 本题考查了一次函数的性质，一次函数的图象经过第几象限，取决于x的系数及常数是大于0或是小于0． 11．（3分）如果关于x的方程=无解，则m=﹣5． 考点： 分式方程的解． 分析： 分式方程无解的条件是：去分母后所得整式方程无解，或解这个整式方程得到的解使原方程的分母等于0．解答： 解：去分母得：x﹣3=m，解得：x=m+3，∵原方程无解，∴最简公分母：x+2=0，解得：x=﹣2，即可得：m=﹣5．故答案为﹣5．点评： 本题考查了分式方程的解，分式方程无解分两种情况：整式方程本身无解；分式方程产生增根． 12．（3分）如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别为2和3，则正方形的边长是． 考点： 全等三角形的判定与性质；勾股定理；正方形的性质． 专题： 计算题．分析： 作AE⊥l于E，CF⊥l于F，如图，AE=2，CF=3，利用正方形的性质得BA=BC，∠ABC=90°，再利用等角的余角相等得∠CBF=∠BAE，则可根据“AAS”判定△ABE≌△BCF，所以AE=BF=2，然后在Rt△BCF中，利用勾股定理计算BC的长即可．解答： 解：作AE⊥l于E，CF⊥l于F，如图，AE=2，CF=3，∵四边形ABCD为正方形，∴BA=BC，∠ABC=90°，∴∠ABE+∠CBF=90°，而∠ABE+∠BAE=90°，∴∠CBF=∠BAE，在△ABE和△BCF中，∴△ABE≌△BCF，∴AE=BF=2，在Rt△BCF中，BC===，即正方形的边长为．故答案为．点评： 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了正方形的性质和勾股定理．本题的关键的作辅助线构造两个全等的三角形． 13．（3分）菱形的两对条角线长分别为10cm、24cm，则它的周长为42cm． 考点： 菱形的性质． 分析： 根据菱形的对角线互相垂直且平分可求得菱形的边长，则可求得其周长．解答： 解：如图，在菱形ABCD中，AC=10cm，BD=24cm，且AC、BD交于点O，∵四边形ABCD为菱形，∴AO=AC=5cm，BO=BD=12cm，且AC⊥BD，在Rt△AOB中，由勾股定理可得AB===13（cm），且菱形的四边相等，∴菱形的周长=4AB=42cm，故答案为：42．点评： 本题主要考查菱形的性质，根据菱形的对角线互相垂直且平分求得菱形的边长是解题的关键． 14．（3分）某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是88分． 考点： 加权平均数． 分析： 按3：3：4的比例算出本学期数学学期综合成绩即可．解答： 解：本学期数学学期综合成绩=90×30%+90×30%+85×40%=88（分）．故答案为：88．点评： 本题考查了加权成绩的计算，平时成绩：期2015届中考试成绩：期末考试成绩=3：3：4的含义就是分别占总数的30%、30%、40%． 15．（3分）如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于点P．若四边形ABCD的面积是4，则DP的长是2． 考点： 全等三角形的判定与性质． 专题： 计算题．分析： 作DE⊥BC，交BC延长线于E，如图，则四边形BEDP为矩形，再利用等角的余角相等得到∠ADP=∠CDE，则可利用“AAS”证明△ADP≌△CDE，得到DP=DE，S△ADP=S△CDE，所以四边形BEDP为正方形，S四边形ABCD=S矩形BEDP，根据正方形的面积公式得到DP2=4，易得DP=2．解答： 解：作DE⊥BC，交BC延长线于E，如图，∵DP⊥AB，ABC=90°，∴四边形BEDP为矩形，∴∠PDE=90°，即∠CDE+∠PDC=90°，∵∠ADC=90°，即∠ADP+∠PDC=90°，∴∠ADP=∠CDE，在△ADP和△CDE中，∴△ADP≌△CDE，∴DP=DE，S△ADP=S△CDE，∴四边形BEDP为正方形，S四边形ABCD=S矩形BEDP，∴DP2=4，∴DP=2．故答案为2．点评： 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了正方形的性质和勾股定理．本题的关键的作辅助线构造两个全等的三角形． 三、解答题16．（10分）计算（1）|﹣1|﹣（π﹣3）0+（）﹣1（2）﹣． 考点： 分式的加减法；零指数幂；负整数指数幂． 专题： 计算题．分析： （1）原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算，第三项利用负整数指数幂法则计算即可得到结果；（2）原式通分并利用同分母分式的减法法则计算即可得到结果．解答： 解：（1）原式=1﹣1+2=2；（2）原式==．点评： 此题考查了分式的加减法，以及实数的运算，熟练掌握运算法则是解本题的关键． 17．（8分）已知一个一次函数的图象与一个反比例函数的图象交于点P（﹣2，1）、Q（1，m）．（1）分别求出这两个函数的表达式．（2）在同一平面直角坐标系中画出这两个函数的图象，根据图象回答，当x取何值时，一次函数的值大于反比例函数的值？ 考点： 反比例函数与一次函数的交点问题． 分析： （1）设出反比例函数关系式，利用代定系数法把P（﹣2，1）代入函数解析式即可．由于Q点也在反比例函数图象上，所以把Q点坐标代入反比例函数解析式中即可得到Q点坐标，求出m的值，利用待定系数法求一次函数解析式；（2）根据图象可得到答案，注意反比例函数图象与y轴无交点，所以分开看．解答： 解：（1）设反比例函数的解析式为y=∵反比例函数经过点P（﹣2，1），∴a=﹣2×1，∴a=﹣2，∴反比例函数的解析式为y=﹣，∵Q（1，m）在反比例函数图象上，∴m=﹣2，设一次函数的解析式为y=kx+b∵P（﹣2，1），Q（1，﹣2）在一次函数图象上∴，∴，∴一次函数的解析式为y=﹣x﹣1；（2）如图所示：由图可知：当0＜x＜1或x＜﹣2时一次函数的值大于反比例函数的值．点评： 此题主要考查了利用待定系数法求反比例函数解析式与一次函数解析式，画函数图象，正确的识别图形是解题的关键． 18．（9分）如图，在▱ABCD中，点E为CD的中点，连接BE并延长交AD的延长线于点F．求证：点E是BF的中点，点D是AF的中点． 考点： 平行四边形的性质；全等三角形的判定与性质． 专题： 证明题．分析： 由在▱ABCD中，点E为CD的中点，易证得△BCE≌△FDE（AAS），然后由全等三角形的对应边相等，证得结论．解答： 证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠CBE=∠F，∵点E为CD的中点，∴CE=DE，在△BCE和△FDE中，，∴△BCE≌△FDE（AAS），∴BE=FE，BC=DF，∴AD=DF，即点E是BF的中点，点D是AF的中点．点评： 此题考查了平行四边形的性质以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用． 19．（8分）如图，在矩形ABCD中，对角线AC与BD相交于点O，AE垂直且平分线段BO，垂足为点E，BD=15cm，求AC、AB的长． 考点： 矩形的性质；线段垂直平分线的性质． 分析： 由矩形的性质得出AC=BD=15cm，OA=OB=7.5cm，由线段垂直平分线的性质得出AB=OA即可．解答： 解：∵四边形ABCD是矩形，∴AC=BD=15cm，OA=AC，OB=BD，∴OA=OB=7.5cm，∵AE垂直且平分线段BO，∴AB=OA=7.5cm．点评： 本题考查了矩形的性质、线段垂直平分线的性质；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键． 20．（9分）如图，在△ABC中，AB=AC，点D是BC的中点，DE⊥AC于点E，DG⊥AB于点G，EK⊥AB于点K，GH⊥AC于点H、EK和GH相交于点F．求证：GE与FD互相垂直平分． 考点： 菱形的判定与性质． 专题： 证明题．分析： 先求出四边形是平行四边形，证三角形全等，得出DG=DE，根据菱形的判定得出即可．解答： 证明：∵DE⊥AC，DG⊥AB，EK⊥AB，GH⊥AC，∴∠DGB=∠DEC=90°，EK∥DG，DE∥GH，∴四边形DEFG是平行四边形，∵AB=AC，∴∠B=∠C，在△DGB和△DEC中，，∴△DGB≌△DEC（AAS），∴DG=DE，∵四边形DEFG是平行四边形，∴四边形DEFG是菱形，∴GE与FD互相垂直平分．点评： 本题考查了全等三角形的性质和判定，菱形的判定，平行四边形的判定的应用，主要考查学生的推理能力，注意：有一组邻边相等的平行四边形是菱形． 21．（9分）如图，在正方形ABCD中，CE⊥DF，求证：CE=DF． 考点： 全等三角形的判定与性质；正方形的性质． 专题： 证明题．分析： 由在正方形ABCD中，CE⊥DF，易证得△BCE≌△CDF（ASA），即可证明．解答： 证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠DCF=90°，∴∠BCE+∠DCE=90°，∵CE⊥DF，∴∠DCE+∠CDF=90°，∴∠BCE=∠CDF，在△BCE和△CDF中，，∴△BCE≌△CDF（ASA），∴DF=CE．点评： 此题考查了正方形的性质以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用． 22．（10分）某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：加工件数 540 450 300 240 210 120人数 1 1 2 6 3 2（1）写出这15人该月加工零件数的平均数、中位数和众数．（2）假如生产部负责人把每位工人的月加工零件数定为260（件），你认为这个定额是否合理，为什么？ 考点： 中位数；算术平均数；众数． 专题： 应用题．分析： （1）平均数=加工零件总数÷总人数，中位数是将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．本题中应是第7个数．众数又是指一组数据中出现次数最多的数据．240出现6次．（2）应根据中位数和众数综合考虑．解答： 解：（1）平均数：=260（件）；中位数：240（件）；众数：240（件）； （2）不合理，因为表中数据显示，每月能完成260件的人数一共是4人，还有11人不能达到此定额，尽管260是平均数，但不利于调动多数员工的积极性，因为240既是中位数，又是众数，是大多数人能达到的定额，故定额为240较为合理．点评： 在做本题的平均数时，应注意先算出15个人加工的零件总数．为了大多数人能达到的定额，制定标准零件总数时一般应采用中位数或众数． 23．（12分）已知：如图，在△ABC中，D是BC边上的一点，连接AD，取AD的中点E，过点A作BC的平行线与CE的延长线交于点F，连接DF．（1）求证：AF=DC；（2）若AD=CF，试判断四边形AFDC是什么样的四边形？并证明你的结论． 考点： 矩形的判定；全等三角形的判定与性质． 专题： 证明题．分析： （1）因为AF∥DC，E为AD的中点，即可根据AAS证明△AEF≌△DEC，故有AF=DC；（2）由（1）知，AF=DC且AF∥DC，可得四边形AFDC是平行四边形，又因为AD=CF，故可根据对角线相等的平行四边形是矩形进行判定．解答： 证明：（1）∵AF∥DC，∴∠AFE=∠DCE，又∵∠AEF=∠DEC（对顶角相等），AE=DE（E为AD的中点），∴△AEF≌△DEC（AAS），∴AF=DC； （2）矩形．由（1），有AF=DC且AF∥DC，∴四边形AFDC是平行四边形，又∵AD=CF，∴AFDC是矩形（对角线相等的平行四边形是矩形）．点评： 本题考查矩形的判定和全等三角形的判定与性质．要熟知这些判定定理才会灵活运用，根据性质才能得到需要的相等关系．