2021河北省深州市长江中学高一下学期期中考试数学试题图片版含答案

参考答案

1．D【详解】由题意，对应点为，在第四象限．故选：D．

2.B 【详解】，

，

所以，.故选：B.

3．B【详解】由已知，所以，故选：B．

【点睛】本题考查平面向量模的坐标运算，掌握向量模的坐标表示是解题关键，本题属于基础题．

4．C【详解】∵ 向量，

∴

∵

∴，即

∴故选C

5．B【详解】

因为，

所以在复平面内，对应的点的坐标是.故选：B

【点睛】本题主要考查复数的运算及几何意义，还考查了运算求解的能力，属于基础题.

6．A设球半径为，则，，而，所以是球的直径，球心是中点，

，所以中点是直角外心，所以平面，又平面，所以，

，，，

是中点，

所以．

故选：A．

7．A解析：因为ABD是以BD为斜边的等腰直角三角形，所以DA⊥AB，又因为平面ABD⊥平面ABC，平面ABD 平面ABC ，

所以DA⊥平面ABC，所以DA⊥AC，可得DA，BA，CA两两垂直，且DA=BA=CA=，构造正方体如图所示，

可得四面体ABCD的外接球半径，

所以表面积为.

故选：A

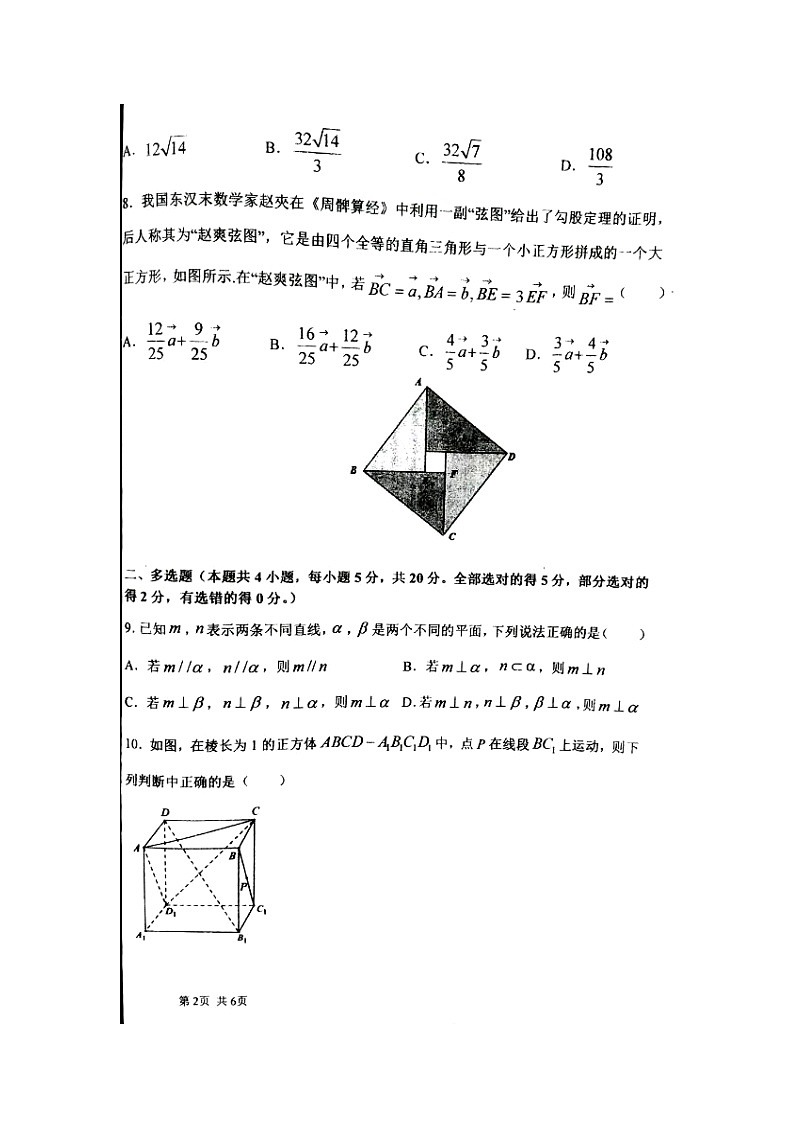
8．B由题得

即，解得，即，故选：B

【点睛】方法点睛：向量的线性运算，一般主要考查平面向量的加法、减法法则、平行四边形法则和数乘向量，要根据已知条件灵活运算这些知识求解.

9．BC

对于选项A，若，，则与可能相交､平行或异面，A错误；

由直线与平面垂直的性质得选项B正确；

依据直线与平面垂直的性质定理得C正确；

选项D中可能与平面平行､垂直､斜交或在平面内.

故选：BC

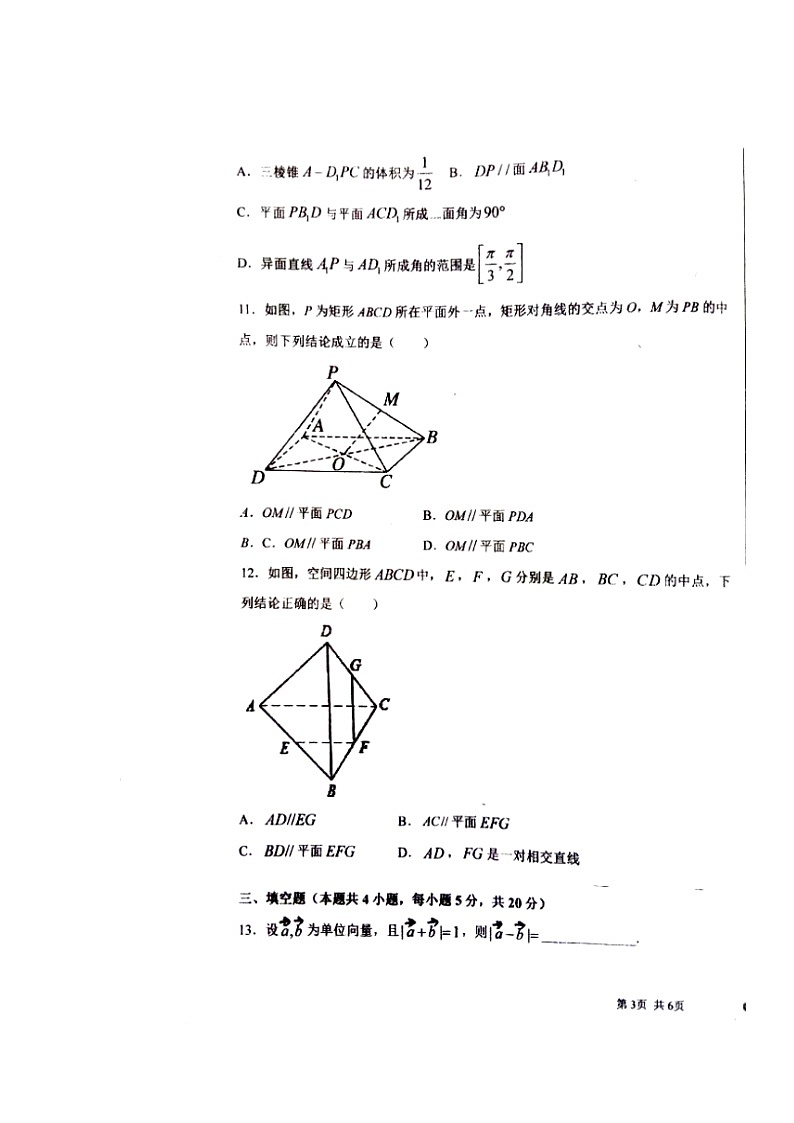
10．BCD

A：，因为到面的距离不变，且△的面积不变，所以三棱锥的体积不变，当与重合时得，错误；

B：连接，，，，易证面面，又面，所以面，正确；

C：根据正方体的结构特征，有面，又面，则面面，正确；

D：由知：当与线段的两端点重合时，与所成角取最小值，当与线段的中点重合时，与所成角取最大值，故与所成角的范围，正确.

11．AB

矩形ABCD的对角线AC与BD交于点O，所以点O为BD的中点，在△PBD中，因为点M是PB的中点，所以OM是△PBD的中位线，OM//PD，平面，平面，平面，故正确；

平面，平面，平面，故B正确；

因为MPB，平面，平面，所以OM与平面，平面相交，故CD错误；故选：AB.

12．BC

A：点平面，点直线，点平面，由异面直线的定义可知，是异面直线，A错；

B：，由直线与平面平行的判定定理可得平面，答案B对；

C：，由直线与平面平行的判定定理可得平面，答案C对；

D：点平面，点直线，点平面，由异面直线的定义可知，是异面直线，D错；

故选：BC.

13． 因为为单位向量，所以

所以

解得：

所以

故答案为：

14．

由，根据同角三角函数关系式得

，解得

所以 ，因为，，

由余弦定理

代入得

所以△ABC为等腰三角形，且 ，

由正弦定理得外接圆半径为 ，解得，

设外心为 ， ，过 作，

设外接球的半径为 则在 中

在中 解得

所以外接球面积为.

故答案为：

15．  设球的半径为，因为球的表面积为，所以，所以球的半径，

因为正方体的所有顶点在一个球面上，所以正方体的对角线长为，

设正方体的棱长为，则，所以.

所以正方体的体积为.

故答案为：

16．

因为，所以，所以，

所以

故答案为：..

17．

的顶点坐标分别为，

，，，，

同理可得：，满足，

是以为直角的直角三角形，

,，，

18．（1）；（2）详见解析.

解：（1）因为

所以

所以

（2）因为

所以.

所以

19．（Ⅰ）；（Ⅱ）.

【详解】解：（Ⅰ）∵，

∴为等边三角形，∴.

又，∴，

∴点在底面上的射影是等边的外心，

∴.

（Ⅱ）由（Ⅰ）可知底面，

且底面，∴.

又，，∴，

∴.

21．（1）证明见解析（2）（3）

证明：（1）连接，交于点，连接.

四棱锥为正四棱锥，

四边形为正方形，为中点，

为中点，为的中位线，

，

平面，平面，

平面.

（2）在正四棱锥中，平面，

即棱锥的高为，

在中，,

故.

22..