

2020-2021学年浙江省杭州市高一(下)期末数学试卷
展开2020-2021学年浙江省杭州市高一(下)期末数学试卷
一.选择题:本大题共8小题,每小题5分,共40分.每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分.
1.(5分)设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
A.{x|﹣2<x<1} B.{x|﹣2<x<2} C.{x|1<x<2} D.{x|x<2}
2.(5分)设复数z满足zi=1﹣2i(i是虚数单位),则z=( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
3.(5分)已知a=log20.2,b=20.2,c=sin2,则( )
A.a<b<c B.a<c<b C.c<a<b D.b<c<a
4.(5分)风光秀丽的千岛湖盛产鳙鱼,记鳙鱼在湖中的游速为vm/s,鳙鱼在湖中的耗氧量的单位数为x,已知鳙鱼的游速v与log2(x≥100)成正比,当鳙鱼的耗氧量为200单位时,其游速为m/s.若某条鳙鱼的游速提高了1m/s,那么它的耗氧量的单位数是原来的( )
A.2倍 B.4倍 C.6倍 D.8倍
5.(5分)两个体积分别为V1,V2的几何体夹在两个平行平面之间,任意一个平行于这两个平面的平面截这两个几何体,截得的截面面积分别为S1,S2,则“V1=V2“是“S1=S2”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.(5分)如图,一个半径为2的水轮,圆心O距离水面1米,水轮做匀速圆周运动,每分钟逆时针旋转4圈.水轮上的点P到水面的距离y(米)与时间x(秒)满足y=Asin(ωx+φ)+k(A>0),则( )
A.ω B.A=3 C.k=2 D.φ=0
7.(5分)如图是第24届国际数学家大会的会标,是根据中国古代数学家赵爽的弦图设计的.已知图中正方形ABCD的边长为1,∠DAE=θ,则小正方形EFGH的面积为( )
A.1﹣sin2θ B.1﹣cos2θ C.1﹣2sinθ D.1﹣2cosθ
8.(5分)设x0∈R,△x>0,函数f(x)满足,n∈N*,则函数y=f(x)可能是(其中a>0且a≠1)( )
A.f(x)=ax B.f(x)=xa C.f(x)=ax D.f(x)=logax
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
(多选)9.(5分)已知不等式ax2+bx+c≥0的解集是{x|﹣1≤x≤2},则( )
A.b<0 B.a+b+c>0 C.c>0 D.a+b=0
(多选)10.(5分)已知平面向量,,若||=3,||,•6,则( )
A.
B.向量与向量的夹角为
C.
D.向量与向量的夹角为
(多选)11.(5分)已知某湖泊蓝藻面积y(单位:m2)与时间t(单位:月)满足y=at.若第1个月的蓝藻面积为2m2,则( )
A.蓝藻面积每个月的增长率为100%
B.蓝藻每个月增加的面积都相等
C.第6个月时,蓝藻面积就会超过60m2
D.若蓝藻面积到2m2,3m2,6m2所经过的时间分别是t1,t2,t3,则t1+t2=t3
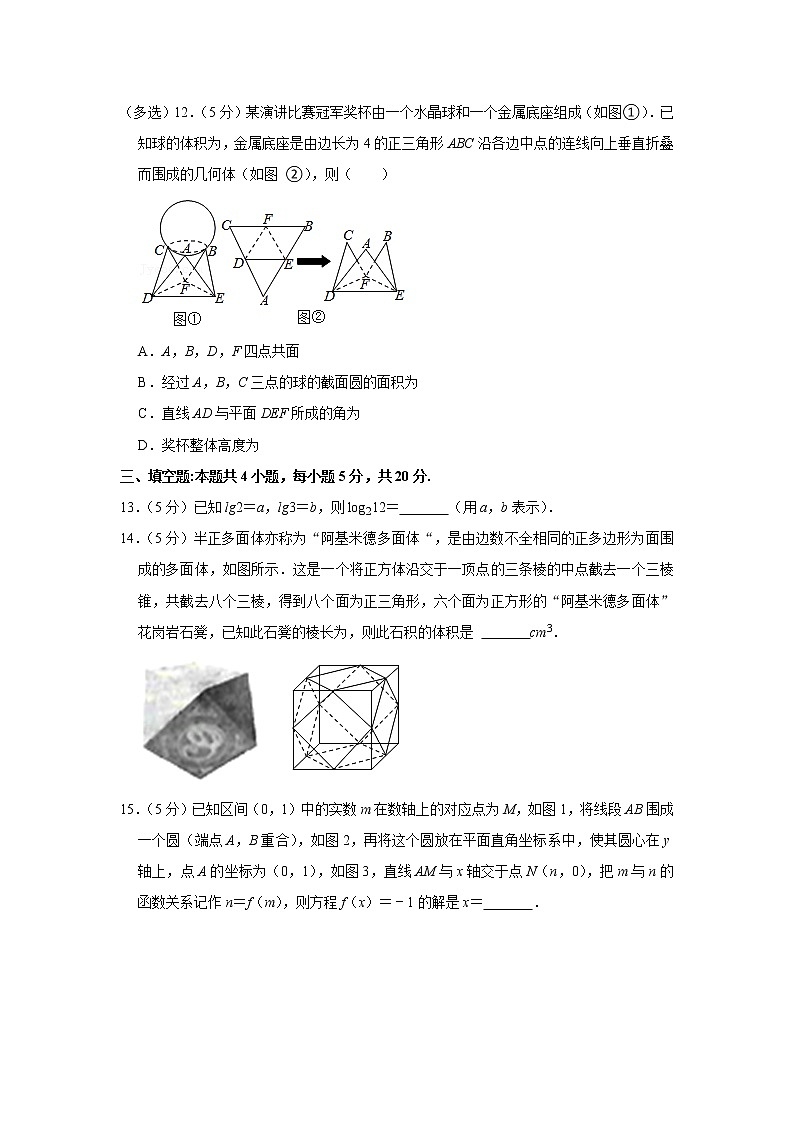
(多选)12.(5分)某演讲比赛冠军奖杯由一个水晶球和一个金属底座组成(如图①).已知球的体积为,金属底座是由边长为4的正三角形ABC沿各边中点的连线向上垂直折叠而围成的几何体(如图 ②),则( )
A.A,B,D,F四点共面
B.经过A,B,C三点的球的截面圆的面积为
C.直线AD与平面DEF所成的角为
D.奖杯整体高度为
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)已知lg2=a,lg3=b,则log212= (用a,b表示).
14.(5分)半正多面体亦称为“阿基米德多面体“,是由边数不全相同的正多边形为面围成的多面体,如图所示.这是一个将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共截去八个三棱,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”花岗岩石凳,已知此石凳的棱长为,则此石积的体积是 cm3.
15.(5分)已知区间(0,1)中的实数m在数轴上的对应点为M,如图1,将线段AB围成一个圆(端点A,B重合),如图2,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3,直线AM与x轴交于点N(n,0),把m与n的函数关系记作n=f(m),则方程f(x)=﹣1的解是x= .
16.(5分)已知||=1,向量满足||•,当向量,夹角最大时,||= .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①a,②ScosB,③C这三个条件中任选﹣一个,补充在下面问题中,并对其进行求解.
问题:在△ABC中,内角A,B,C的对边分别为a,b,c,面积为S,bcosA=acosC+ccosA,b=1,_____,求c的值.
18.(12分)如图,在△OAB中,P为边AB上的一点,且与的夹角为60°.
(1)设,求x,y的值;
(2)求的值.
19.(12分)四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,∠A1AB=∠A1AD=∠BAD=60°.
(1)求证:AA1⊥BD;
(2)求直线A1B与平面AA1D1D所成角的正弦值.
20.(12分)如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象,f(0)=f(),f()=0.
(1)求f(x)的解析式;
(2)将f(x)的图象向右平移,得函数g(x),记h(x)=f(x)+g(x),求h(x)的单调递减区间.
21.(12分)将一张长8cm,宽6cm的长方形纸片沿着直线MN折叠,折痕MN将纸片分成两部分,面积分别为S1cm2,S2cm2.设MN=lcm.若S1:S2=1:2,求l的取值范围.
22.(12分)设函数f(x)=x|x﹣a|+a|x﹣2|(a>0),方程f(x)=t有三个不同的实数根x1,x2,x3,且x1<x2<x3.
(1)当a=2时,求实数t的取值范围;
(2)当t=2时,求正数a的取值范围;
(3)在(2)的条件下,若恒成立,求实数λ的取值范围.
2020-2021学年浙江省杭州市高一(下)期末数学试卷
参考答案与试题解析
一.选择题:本大题共8小题,每小题5分,共40分.每小题列出的四个选项中只有一个是符合题目要求的,不选、多选、错选均不得分.
1.(5分)设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
A.{x|﹣2<x<1} B.{x|﹣2<x<2} C.{x|1<x<2} D.{x|x<2}
【解答】解:∵M={x||x|≥2}={x|x≥2或x≤﹣2}N={x|1<x<3}
∵阴影部分表示集合(∁UM)∩N,
∴阴影部分表示的集合是(1,2).
故选:C.
2.(5分)设复数z满足zi=1﹣2i(i是虚数单位),则z=( )
A.2+i B.2﹣i C.﹣2+i D.﹣2﹣i
【解答】解:因为复数z满足zi=1﹣2i,
所以.
故选:D.
3.(5分)已知a=log20.2,b=20.2,c=sin2,则( )
A.a<b<c B.a<c<b C.c<a<b D.b<c<a
【解答】解:∵,
∴a<c<b,
故选:B.
4.(5分)风光秀丽的千岛湖盛产鳙鱼,记鳙鱼在湖中的游速为vm/s,鳙鱼在湖中的耗氧量的单位数为x,已知鳙鱼的游速v与log2(x≥100)成正比,当鳙鱼的耗氧量为200单位时,其游速为m/s.若某条鳙鱼的游速提高了1m/s,那么它的耗氧量的单位数是原来的( )
A.2倍 B.4倍 C.6倍 D.8倍
【解答】解:∵鳙鱼的游速v与log2(x≥100)成正比,
∴,
∵当x=200时,v,
∴,解得k,
∴,
设鳙鱼开始的速度为v0,耗氧的单位数为x0,提速后的速度为v1,提速后的耗氧的单位数为x1,
∵
又∵,
∴x1=4x0,
故选:B.
5.(5分)两个体积分别为V1,V2的几何体夹在两个平行平面之间,任意一个平行于这两个平面的平面截这两个几何体,截得的截面面积分别为S1,S2,则“V1=V2“是“S1=S2”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解答】解:根据祖暅原理,
①由S1=S2,得到V1=V2,∴必要性成立,
②由V1=V2,则只需要底面积和高相等即可,则S1,S2不一定相等,∴充分性不成立,
∴V1=V2是S1=S2的必要不充分条件,
故选:B.
6.(5分)如图,一个半径为2的水轮,圆心O距离水面1米,水轮做匀速圆周运动,每分钟逆时针旋转4圈.水轮上的点P到水面的距离y(米)与时间x(秒)满足y=Asin(ωx+φ)+k(A>0),则( )
A.ω B.A=3 C.k=2 D.φ=0
【解答】解:∵水轮的半径为2,水轮圆心O距离水面1m,由题意可得,
∴解得A=2,k=1,可得B,C选项错误,
又水轮每分钟旋转4圈,故转一圈需要15秒,
∴T=15,
∴ω,可得A正确,
又由题意,未指明初始位置φ的值无法确定,故D错误.
故选:A.
7.(5分)如图是第24届国际数学家大会的会标,是根据中国古代数学家赵爽的弦图设计的.已知图中正方形ABCD的边长为1,∠DAE=θ,则小正方形EFGH的面积为( )
A.1﹣sin2θ B.1﹣cos2θ C.1﹣2sinθ D.1﹣2cosθ
【解答】解:正方形ABCD中,AD=1,∠DAE=θ,
所以DH=ADsin∠DAE=sinθ,
AH=ADcos∠DAE=cosθ,
又因为Rt△ADH≌Rt△BAE≌Rt△CBF≌Rt△DCG,
所以GH=DH﹣AH=sinθ﹣cosθ,
所以小正方形EFGH的面积为:
S=GH2=(sinθ﹣cosθ)2=sin2θ﹣2sinθcosθ+cos2θ=1﹣sin2θ.
故选:A.
8.(5分)设x0∈R,△x>0,函数f(x)满足,n∈N*,则函数y=f(x)可能是(其中a>0且a≠1)( )
A.f(x)=ax B.f(x)=xa C.f(x)=ax D.f(x)=logax
【解答】解:因为函数f(x)满足,n∈N*,
当f(x)=ax时,a△x.
故选:C.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
(多选)9.(5分)已知不等式ax2+bx+c≥0的解集是{x|﹣1≤x≤2},则( )
A.b<0 B.a+b+c>0 C.c>0 D.a+b=0
【解答】解:不等式ax2+bx+c≥0的解集是{x|﹣1≤x≤2},
所以a<0且,
解得b=﹣a,c=﹣2a;
所以a+b=0,选项D正确;
设二次函数f(x)=ax2+bx+c,且a<0,
且函数的零点是﹣1和2,所以f(1)=a+b+c>0,选项B正确;
因为c=﹣2a>0,所以选项C正确;
因为b=﹣a>0,所以选项A错误.
故选:BCD.
(多选)10.(5分)已知平面向量,,若||=3,||,•6,则( )
A.
B.向量与向量的夹角为
C.
D.向量与向量的夹角为
【解答】解:∵||,
∴13,
∵||=3,•6,
∴,故A选项正确,
,
∴向量与的夹角为,故选项B错误,选项D正确,
9+12+16=37,故选项C错误,
故正确的选项为AD.
故选:AD.
(多选)11.(5分)已知某湖泊蓝藻面积y(单位:m2)与时间t(单位:月)满足y=at.若第1个月的蓝藻面积为2m2,则( )
A.蓝藻面积每个月的增长率为100%
B.蓝藻每个月增加的面积都相等
C.第6个月时,蓝藻面积就会超过60m2
D.若蓝藻面积到2m2,3m2,6m2所经过的时间分别是t1,t2,t3,则t1+t2=t3
【解答】解:由题意可知,函数y=at 图象经过(1,2),即a1=2,
∴a=2,
∴y=2t,
∵2t+1﹣2t=2t,
∴蓝藻每个月的面积时上个月的2倍,
∴每个月的增长率为100%,故A选项正确,
∵2t+1﹣2t=2t,即每个月增长量为2t,非常数,故B选项错误,
当t=6时,y=26=64>60,故C选项正确,
∵若蓝藻面积到2m2,3m2,6m2所经过的时间分别是t1,t2,t3,
∴,
∴t1=log22,t2=log23,t3=log26,
∴t1+t2=log22+log23=log26=t3,故D选项正确.
故选:ACD.
(多选)12.(5分)某演讲比赛冠军奖杯由一个水晶球和一个金属底座组成(如图①).已知球的体积为,金属底座是由边长为4的正三角形ABC沿各边中点的连线向上垂直折叠而围成的几何体(如图 ②),则( )
A.A,B,D,F四点共面
B.经过A,B,C三点的球的截面圆的面积为
C.直线AD与平面DEF所成的角为
D.奖杯整体高度为
【解答】解:根据图形的形成可知,点A,B,C三点在底面DEF上的射影分别是△DEF三边的中点,如图所示,
则△ABC与△MNP全等且所在的面平行,
平面ABNM∩平面ABC=AB,平面ABNM∩平面DEF=MN,
所以MN∥AB,又MN∥DF,
所以AB∥DF,
故A,B,D,F四点共面,
故选项A正确;
因为△ABC与△MNP全等且所在的面平行,所以截面圆就是△ABC的外接圆与△MNP的外接圆相同,
由题意可知,△MNP的边长为1,其外接圆的半径为,
则经过A,B,C三点的球的截面圆的面积为,
故选项B错误;
由平面ADE与平面DEF垂直可知,AE在平面AEF内的射影是DE,
所以∠ADE为直线AD与平面DEF所成的角,则∠ADE,
所以直线AD与平面DEF所成的角为,
故选项C正确;
因为AB=BC=CA=1,设O为球心,半径为R,
则,解得R=1,
所以O﹣ABC是正四面体,棱长为1,
设H为△ABC的外心,则OH⊥平面ABC,
又CH⊂平面ABC,
所以OH⊥CH,
又,则,
又AM,
所以奖杯整体高度为,
故选项D正确.
故选:ACD.
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)已知lg2=a,lg3=b,则log212= (用a,b表示).
【解答】解:∵lg2=a,lg3=b,
∴log212.
故答案为:.
14.(5分)半正多面体亦称为“阿基米德多面体“,是由边数不全相同的正多边形为面围成的多面体,如图所示.这是一个将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共截去八个三棱,得到八个面为正三角形,六个面为正方形的“阿基米德多面体”花岗岩石凳,已知此石凳的棱长为,则此石积的体积是 cm3.
【解答】解:如图所示,该石凳是由棱长为40cm的正方体
沿各棱中点截去8个三棱锥所得到的,
∴该石凳的体积为:Vcm3.
故答案为:cm3.
15.(5分)已知区间(0,1)中的实数m在数轴上的对应点为M,如图1,将线段AB围成一个圆(端点A,B重合),如图2,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3,直线AM与x轴交于点N(n,0),把m与n的函数关系记作n=f(m),则方程f(x)=﹣1的解是x= .
【解答】解:由题意知,N(﹣1,0),A(0,1),
故△NOA为等腰直角三角形,
故∠NAO,故弦AM对应的圆心角为,
故是圆周长的,即m,
故方程f(x)=﹣1的解是x,
故答案为:.
16.(5分)已知||=1,向量满足||•,当向量,夹角最大时,||= .
【解答】解:设(1,0),,
∵||•,
∴,化简后可得y2=2x﹣1,,
∴,
,
设t,即0<t≤2,则,当t=1,即x=1,
取得最小值,即向量,夹角最大时,
∴.
故答案为:.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)在①a,②ScosB,③C这三个条件中任选﹣一个,补充在下面问题中,并对其进行求解.
问题:在△ABC中,内角A,B,C的对边分别为a,b,c,面积为S,bcosA=acosC+ccosA,b=1,_____,求c的值.
【解答】解:在△ABC中,因为,
所以根据正弦定理得,
所以,
因为sinB≠0,
所以,
选择①,由余弦定理a2=b2+c2﹣2bccosA,得,
解得,
选择②,,
所以
所以,即,
解得,
选择③,,因为,
所以由,得c33.
18.(12分)如图,在△OAB中,P为边AB上的一点,且与的夹角为60°.
(1)设,求x,y的值;
(2)求的值.
【解答】解:(1)∵2,∴(),
∴(),
∴x,y.
(2)∵36,2=4,6×2×cos60°=6,
∴()•()242.
19.(12分)四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,∠A1AB=∠A1AD=∠BAD=60°.
(1)求证:AA1⊥BD;
(2)求直线A1B与平面AA1D1D所成角的正弦值.
【解答】(1)证明:取BD的中点O,连结OA,OA1,
因为ABCD为菱形,则BD⊥AO,
因为∠A1AB=∠A1AD,四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,
则A1D=A1B,O为BD的中点,则BD⊥A1O,
又A1O∩AO=O,A1O,AO⊂平面A1AO,
所以BD⊥平面A1AO,
又A1A⊂平面A1AO,
所以BD⊥A1A;
(2)解:由题意可知,B﹣A1AD为正四面体,
在正四面体B﹣A1AD中,设顶点B在底面正三角形A1AD中的射影为O',连结A1O',
则∠BA1O'即为直线A1B与平面AA1D1D所成的角,
设A1B=1,则,则,
在Rt△BA1O'中,sin∠BA1O',
所以直线A1B与平面AA1D1D所成角的正弦值为.
20.(12分)如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象,f(0)=f(),f()=0.
(1)求f(x)的解析式;
(2)将f(x)的图象向右平移,得函数g(x),记h(x)=f(x)+g(x),求h(x)的单调递减区间.
【解答】解:(1)由函数的图象顶点可得A=2,
∵f(0)=f(),
∴f(x)关于x称轴,
那么周期T,
可得T=π,
则ω,
∴y=2sin(2x+φ),图象过点(,﹣2),
可得﹣2=2sin(φ),
∵|φ|<π,
∴φ.
故得f(x)的解析式为;f(x)=2sin(2x).
(2)f(x)的图象向右平移,得y=2sin[2(x)]=2sin2x.
∴函数g(x)=2sin2x,
h(x)=f(x)+g(x)=f(x)=2sin(2x)+2sin2x=2sin2xcos2cos2xsin2sin2x
cos2x+sin2x
=2sin(2x)
令2x,k∈Z,
可得x,
∴h(x)单调递减区间为[,],k∈Z.
21.(12分)将一张长8cm,宽6cm的长方形纸片沿着直线MN折叠,折痕MN将纸片分成两部分,面积分别为S1cm2,S2cm2.设MN=lcm.若S1:S2=1:2,求l的取值范围.
【解答】解:∵长方形的长为8,宽为6,
∴长方形的面积为S=6×8=48,
∵S1:S2=1:2,
∴S1=16,S2=32,
当折痕为情形①时,设AM=x,AN=y,
∴,即xy=32,可得y,
∵0≤x≤8,且,
∴,
由勾股定理可得,,
设g(x),,
观察可知g(x)为对勾函数,
当 时,即x,满足定义域,即g(x)min=32+32=64,
当x=8时,g(x)max=64+16=80,
∴l的取值范围为[],
当折痕为情形②时,设AM=x,DN=y,
∴,即,
∵0≤x≤8,且0,
∴,
∵,
当x时,l2 为最小值36,
当x时,l2 为最大值,
∴l的取值范围为[],
当折痕是情形③时,设BN=x,AM=y,
,即y=4﹣x,
∵0≤x≤6,且0≤4﹣x≤6,
∴0≤x≤4,
∵l2=82+(x﹣y)2=82+4(x﹣2)2,
当x=2时,l2 为最小值64,
当x=4时,l2 为最大值80,
∴l的取值范围为[],
综上所述,l的取值范围为[6,].
22.(12分)设函数f(x)=x|x﹣a|+a|x﹣2|(a>0),方程f(x)=t有三个不同的实数根x1,x2,x3,且x1<x2<x3.
(1)当a=2时,求实数t的取值范围;
(2)当t=2时,求正数a的取值范围;
(3)在(2)的条件下,若恒成立,求实数λ的取值范围.
【解答】解:(1)当a=2时,,
如图所示,
易知f(x)在(﹣∞,0)单调递增,在(0,2)单调递减,在(2,+∞)单调递增,
∴f(2)<t<f(0),则0<t<4;
(2)①当0<a≤2时,,
如图所示,
f(x)在(﹣∞,0)单调递增,在(0,a)单调递减,在(a,+∞)单调递增,
∴f(a)<2<f(0),则2a﹣a2<2<2a,解得1<a≤2;
②当a>2时,,
如图所示,
f(x)在(﹣∞,0)单调递增,在(0,2)单调递减,在(2,+∞)单调递增,
∴f(2)<2<f(0),则2a﹣4<2<2a,解得2<a<3;
综上,正数a的取值范围为(1,3);
(3)由(2)可知,
①当1<a≤2时,f(x)在(﹣∞,0)单调递增,在(0,a)单调递减,在(a,2)单调递增,在(2,+∞)单调递增,
∵f(2)=4﹣2a<2,
∴x1,x2为方程﹣x2+2a=2的两根,则x1+x2=0,x3是方程x2﹣2a=2的正根,则,
∴,则;
②当2<a<3时,同理,x1,x2为方程﹣x2+2a=2的两根,则x1+x2=0,
f(x)在(﹣∞,0)单调递增,在(0,2)单调递减,在(2,a)单调递增,在(a,+∞)单调递增,f(a)=a2﹣2a=(a﹣1)2﹣1,
(i)当f(a)≥2,即时,x3是方程﹣x2+2ax﹣2a=2的较小根,
在单调递减,则,
∴;
(ii)当f(a)<2,即时,x3是方程x2﹣2a=2的正根,故,
∴,则,
综上,.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2022/5/26 10:14:13;用户:高中数学;邮箱:sdgs@xyh.com;学号:28144983
2022-2023学年浙江省杭州市高一(下)期末数学试卷(含解析): 这是一份2022-2023学年浙江省杭州市高一(下)期末数学试卷(含解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
浙江省杭州市2020-2021学年高一下学期期末考试数学试卷及参考答案: 这是一份浙江省杭州市2020-2021学年高一下学期期末考试数学试卷及参考答案,共25页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年浙江省杭州市高二(下)期末数学试卷: 这是一份2020-2021学年浙江省杭州市高二(下)期末数学试卷,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












