2021-2022学年四川省攀枝花市西区八年级（下）期中数学试卷（含解析）

这是一份2021-2022学年四川省攀枝花市西区八年级（下）期中数学试卷（含解析），共18页。试卷主要包含了2×10−7B，14)0；，【答案】C，【答案】B，【答案】A，【答案】D等内容，欢迎下载使用。
2021-2022学年四川省攀枝花市西区八年级（下）期中数学试卷 一．选择题（本题共12小题，共60分）在代数式，，，，中，分式有A. 个 B. 个 C. 个 D. 个某种感冒病毒的直径是米，用科学记数法表示为米．A.  B.  C.  D. 下列图形不能体现是的函数关系的是A.  B.
C.  D. 点关于轴对称点是A.  B.  C.  D. 下列约分正确的是A.  B.  C.  D. 是方程的解，则函数的图象不经过A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限函数中，自变量的取值范围是A.  B.  C. 且 D. 且下列函数中，随的增大而减小的有
；；；．A. 个 B. 个 C. 个 D. 个在同一坐标系中，函数和的图象大致是A.  B.
C.  D. 若点、和分别在反比例函数的图象上，且，则下列判断中正确的是A.  B.  C.  D. 如图，已知动点，分别在轴，轴正半轴上，动点在反比例函数图象上，轴，是以为底边的等腰三角形．当点的横坐标逐渐增大时，的面积将会A. 不变
B. 越来越大
C. 越来越小
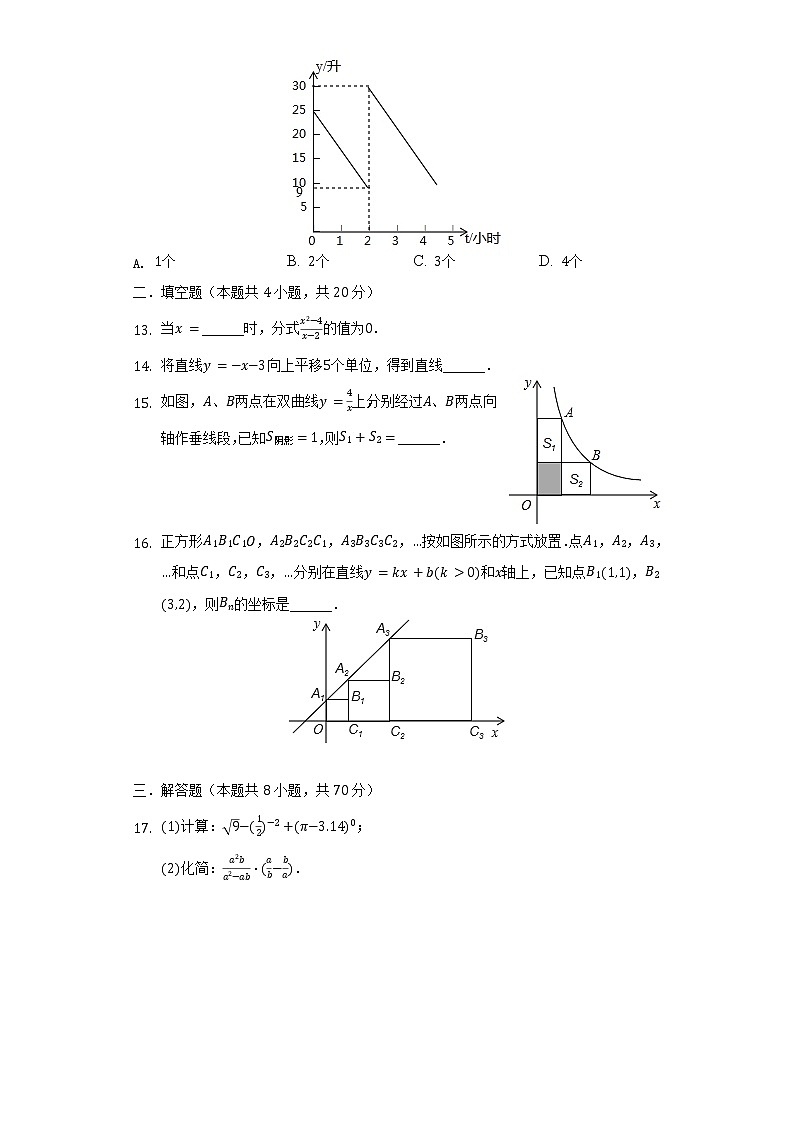
D. 先变大后变小张师傅驾车从甲地到乙地，两地相距千米，汽车出发前油箱有油升，途中加油若干升，加油前、后汽车都以千米小时的速度匀速行驶，已知油箱中剩余油量升与行驶时间小时之间的关系如图，下列四种说法：
加油前油箱中剩余油量升与行驶时间小时的函数关系是；
途中加油升；
汽车加油后还可行驶小时；
汽车到达乙地时油箱中还余油升．
其中正确的个数是
个 B. 个 C. 个 D. 个二．填空题（本题共4小题，共20分）当______时，分式的值为．将直线向上平移个单位，得到直线______．如图，、两点在双曲线上，分别经过、两点向轴作垂线段，已知，则______．

  正方形，，，按如图所示的方式放置．点，，，和点，，，分别在直线和轴上，已知点，，则的坐标是______．
三．解答题（本题共8小题，共70分）计算：；
化简：．






 解分式方程：．






 先化简：，然后在，，，四个数中选择一个你认为最合适的数代入，求值．






 学校准备在甲、乙两家公司为毕业班制作一批纪念册．甲公司提出：收设计费元，另每册收取材料费元；乙公司提出：不收设计费，每册收取材料费元．
写出甲公司的收费元与制作册数的函数关系式；
写出乙公司的收费元与制作册数的函数关系式；
如果学校派你去甲、乙两家公司联系订做纪念册的有关事宜，你会作出怎样的选择才合算？






 列分式方程解应用题
某厂接到一份订单，要求生产顶帐篷支援灾区，后来由于情况紧急，接收到上级指示，要求生产总量比原计划增加，且必须提前天完成生产任务．该厂迅速加派人员组织生产，实际每天生产的顶数是原计划每天生产的顶数的倍，请问该厂实际每天生产多少顶帐篷？






 已知如图，一次函数图象经过点、点求：
这个一次函数的解析式；
一次函数图象与两坐标轴围成的面积．







 “”玉树大地震震惊全中国．面对特大灾害，在党中央国务院的领导下，全国人民万众一心，众志成城，抗震救灾．现在、两市各有赈灾物资吨和吨，急需运往结古镇吨，运往隆宝镇吨，从、两市运往结古镇、隆宝镇的耗油量如表： 结古镇升吨隆宝镇升吨市市若从市运往结古镇的赈灾物资为吨，求完成以上运输所需总耗油量升与吨的函数关系式；
请你求出至少需要多少升油？






 如图，一次函数的图象与反比例函数的图象相交于、两点．
求反比例函数和一次函数的解析式；
求直线与轴的交点的坐标及的面积；
根据图象直接写出使一次函数的值大于反比例函数的值的的取值范围．








答案和解析 1.【答案】
 【解析】解：的分母都含有字母，所以它们是分式，
故选：．
判断分式的依据是看分母中是否含有字母，如果分母中含有字母则是分式，如果不含有字母则不是分式．
本题主要考查分式的定义，认真审题，注意定义，中不是字母，所以它不是分式．
 2.【答案】
 【解析】解：米．
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 3.【答案】
 【解析】解：根据函数的定义可知：对于的任何值都有唯一的值与之相对应，分析图象可知只有不能表示函数关系．
故选：．
函数的意义反映在图象上简单的判断方法是：做垂直轴的直线在左右平移的过程中与函数图象只会有一个交点的图象是函数图象，否则不是．
主要考查了函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．
 4.【答案】
 【解析】解：点关于轴对称点是，
故选：．
根据关于轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得答案．
此题主要考查了关于轴对称点的坐标，关键是掌握点的坐标的变化规律．
 5.【答案】
 【解析】【分析】
此题主要考查了分式的约分，注意：找出分子分母公因式时，常数项也不能忽略，观察分子分母，提取公共部分约分即可．
【解答】解：原式，故本选项错误；
B.原式，故本选项正确；
C.原式，故本选项错误；
D.原式，故本选项错误；
故选B．  6.【答案】
 【解析】解：把代入得，解得，
所以函数为，
函数的图象经过第二、三、四象限，
所以函数的图象不经过第一象限．
故选：．
先把代入得，则函数为，然后根据一次函数的性质求解．
本题考查了一次函数与一元一次方程：当某个一次函数的值为时，求相应的自变量的值．从图象上看，相当于已知直线确定它与轴的交点的横坐标的值．也考查了一次函数的性质．
 7.【答案】
 【解析】【分析】
本题考查的是函数自变量取值范围的求法．函数自变量的范围一般从三个方面考虑：
当函数表达式是整式时，自变量可取全体实数；
当函数表达式是分式时，考虑分式的分母不能为；
当函数表达式是二次根式时，被开方数非负．
根据二次根式的性质和分式的意义，被开方数大于等于，分母不为，列不等式组求解．
【解答】
解：根据题意得：，解得且，
故选D．  8.【答案】
 【解析】解：，；，；，；，．
所以四函数都是随的增大而减小．
故选：．
分别确定四个函数的值，然后根据一次函数的性质判断即可．
本题考查了一次函数的性质：当，随的增大而增大；当，随的增大而减小．
 9.【答案】
 【解析】解：分两种情况讨论：
当时，与轴的交点在正半轴，过一、二、三象限，的图象在第一、三象限；
当时，与轴的交点在正半轴，过一、二、四象限，的图象在第二、四象限．
故选C．
根据一次函数和反比例函数的特点，，所以分和两种情况讨论．当两函数系数取相同符号值，两函数图象共存于同一坐标系内的即为正确答案．
本题主要考查了反比例函数的图象性质和一次函数的图象性质，关键是由的取值确定函数所在的象限．
 10.【答案】
 【解析】解：由题意，得点、在第二象限，在第四象限，
最小，
，
，
．
故选：．
判断出各个点所在的象限，根据反比例函数的增减性可得其中两组点的大小关系，进而比较同一象限点的大小关系即可．
考查反比例函数图象上点的坐标的特点；用到的知识点为：第二象限点的纵坐标总大于第四象限点的纵坐标；在同一象限内，比例系数小于，随的增大而增大．
 11.【答案】
 【解析】解：如图，过点作于点，

则，
设点，
则，
当点的横坐标逐渐增大时，的面积将会不变，始终等于，
故选：．
设点，作可得，根据可得答案．
本题主要考查反比例函数系数的几何意义，熟练掌握在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是，且保持不变．
 12.【答案】
 【解析】解：由题意得，图象过，
设加油前油箱中剩余油量升与行驶时间小时的函数关系是：，
，
解得：，
加油前油箱中剩余油量升与行驶时间小时的函数关系是：，故正确；

途中加油升，故正确；

汽车耗油量为：升小时，
，
汽车加油后还可行驶小时，故错误；

从甲地到乙地，两地相距千米，加油前、后汽车都以千米小时的速度匀速行驶，
需要：小时到达，
汽车到达乙地时油箱中还余油升，故正确；
故选：．
首先利用待定系数法求出函数解析式，进而利用图象求出耗油量以及行驶时间即可．
此题主要考查了一函数应用以及待定系数法求一次函数解析式等知识，根据已知图象获取正确信息是解题关键．
 13.【答案】
 【解析】解：，
．
故答案为：．
分式的值为的条件是：分子；分母两个条件需同时具备，缺一不可．据此可以解答本题．
此题考查的是对分式的值为的条件，分子等于，分母不能等于，题目比较简单．
 14.【答案】
 【解析】解：由“上加下减”的原则可知，将直线向上平移个单位所得直线的解析式为：，即．
故答案为：．
直接根据“上加下减”的原则进行解答即可．
本题考查的是一次函数的图象与几何变换，熟知“上加下减”的原则是解答此题的关键．
 15.【答案】
 【解析】解：点、是双曲线上的点，分别经过、两点向轴、轴作垂线段，
则根据反比例函数的图象的性质得两个矩形的面积都等于，
．
故答案为．
欲求，只要求出过、两点向轴、轴作垂线段求出与坐标轴所形成的矩形的面积即可，而矩形面积为双曲线的系数，由此即可求出．
本题主要考查了反比例函数的图象和性质及任一点坐标的意义，有一定的难度．
 16.【答案】
 【解析】【分析】
本题主要考查函数图象上点的坐标特征及正方形的性质，解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加或倍数情况的变化，找出数量上的变化规律，从而推出一般性的结论．由图和条件可知，，由此可以求出直线为，的横坐标为的横坐标，纵坐标为的纵坐标，又的横坐标为，所以纵坐标为，然后就可以求出的坐标为的横坐标，的纵坐标．
【解答】
解：点，，
，，
直线为，
，
的横坐标为的横坐标，纵坐标为的纵坐标
又的横坐标为，所以纵坐标为，
的坐标为的横坐标，的纵坐标，
故答案为：  17.【答案】解：原式；
原式．
 【解析】原式第一项利用平方根定义化简，第二项利用负指数幂法则计算，第三项利用零指数幂法则计算即可得到结果；
原式括号中两项通分并利用同分母分式的减法法则计算，约分即可得到结果．
此题考查了实数的运算，以及分式的乘除法，熟练掌握运算法则是解本题的关键．
 18.【答案】解：，
，
解得：，
检验：当时，，
是原方程的增根，
原方程无解．
 【解析】按照解分式方程的步骤，进行计算即可解答．
本题考查了解分式方程，一定要注意解分式方程，必须检验．
 19.【答案】解：原式
，
分式有意义，，，
．
当时，原式．
 【解析】先计算括号里分式减法，再将除法转化为乘法计算，最后代入合适的求值即可．
本题考查分式的化简求值，解题关键是熟知分式混合运算的计算法则．
 20.【答案】解：；

；

，
解得；
，
解得；
，
解得．
答：当制作本时，两家公司收费一样；当制作少于本时，选择乙公司比较合算；当制作超过本时，选择甲公司比较合适．
 【解析】甲公司的收费为：设计费总材料费；
乙公司的收费为：制作册数；
让得到的个关系式分别相等，大于，小于求得合适的选择即可．
考查一次函数的应用；注意应用一次函数的解析式判断选择方案问题．
 21.【答案】解：设该厂原计划每天生产顶帐篷，实际每天生产顶帐篷，
由题意得：，
解得：，
经检验：是原方程的解，且符合题意，
则．
答：该厂实际每天生产顶帐篷．
 【解析】设该厂原计划每天生产顶帐篷，实际每天生产顶帐篷，由等量关系：实际每天生产的顶数是原计划每天生产的顶数的倍，且实际所用时间比原计划少天，列出分式方程，解方程即可．
本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．
 22.【答案】解：依题意，
当时，；
当时，．
则
解之得
一次函数解析式为：．
一次函数图象与轴、轴分别相交于、两点，
由，得
点坐标，点坐标，
即，．
．
即一次函数图象与两坐标轴围成的面积为．
 【解析】此题主要考查了待定系数法求一次函数解析式、一次函数的应用、三角形的面积的知识，读懂图象是关键．本题中用待定系数法求出函数解析式是解题的基础．
由图可知，函数经过了和两点，可用待定系数法来求出函数的解析式．
一次函数与两坐标轴围成的是个直角三角形，且直角边的长分别是、两点的纵坐标和横坐标的绝对值．那么只要求出、的坐标即可得出三角形的面积，根据中求出的函数关系式，、的坐标就可以求出来了．
 23.【答案】解：由题意得：，
整理得；
要使最小，则要取最大值，
即，代入得升．
 【解析】根据总耗油量市运往结古镇和隆宝镇的耗油量的和市运往结古镇和隆宝镇的耗油量的和可得关系式；
根据函数的性质来判断出耗油量最少的方案．
本题主要考查了一次函数关系式的应用，根据题意列出关系式是解题关键，注意自变量的取值范围不能遗漏．
 24.【答案】解：把代入得
反比例函数的解析式为，
又在反比例图象上，得，

把和代入，
，
一次函数的解析式为；

当时，得，
与轴的交点坐标是，


；

当或时，一次函数值大于反比例函数值．
 【解析】根据待定系数法，可得反比例函数解析式，根据在函数图象上，可得点的坐标，根据待定系数法，可得一次函数的解析式；
根据一次函数的纵坐标为，可得点的坐标，根据三角形的和差，可得答案；
根据函数图象，找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可．
本题考查了反比例函数与一次函数的交点问题，待定系数法是求反比例函数解析式、一次函数解析式的关键．