2022届贵州省贵阳一中（贵阳市）高三适应性考试（二）数学（文）试题含解析

这是一份2022届贵州省贵阳一中（贵阳市）高三适应性考试（二）数学（文）试题含解析，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
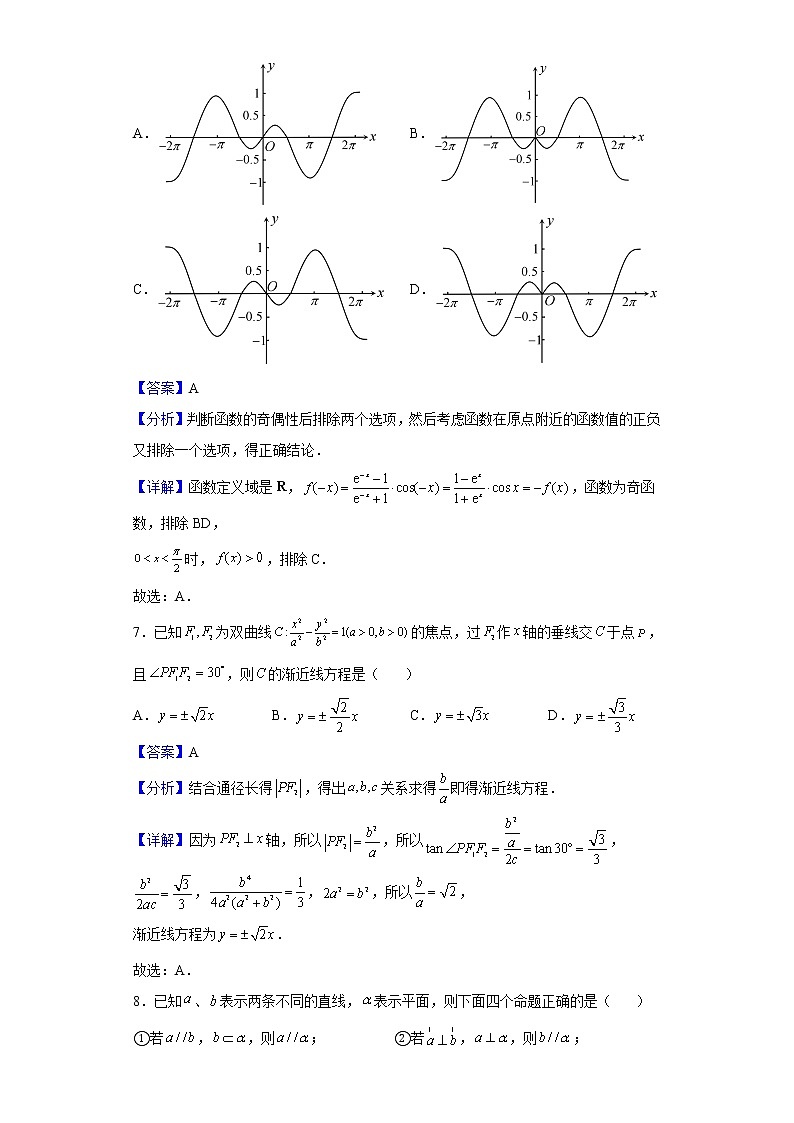
2022届贵州省贵阳市高三适应性考试（二）数学（文）试题一、单选题1．设全集，集合，，则（       ）A． B． C． D．【答案】C【分析】根据集合的运算法则计算．【详解】由已知，所以．故选：C．2．已知为虚数单位，复数满足，则（       ）A．2 B． C． D．【答案】D【分析】由复数的乘方与除法运算计算．【详解】由已知，故选：D．3．已知变量与正相关，且由观测数据算得样本平均数，，则由该观测的数据算得的线性回归方程可能是（    ）A． B．C． D．【答案】A【详解】试题分析：因为与正相关，排除选项C、D，又因为线性回归方程恒过样本点的中心，故排除选项B；故选A．【解析】线性回归直线.4．2021年11月24日，贵阳市修文县发生了4.6级地震，所幸的是没有人员伤亡和较大财产损失，在抗震分析中，某结构工程师提出：由于实测地震记录的缺乏，且考虑到强震记录数量的有限性和地震动的不可重复性，在抗震分析中还需要人工合成符合某些指定统计特征的非平稳地震波时程，其中地震动时程强度包络函数，（单位：秒）分别为控制强震平稳段的首末时刻；（单位：秒）表示地震动总持时；是衰减因子，控制下降段衰减的快慢．在一次抗震分析中，地震动总持时是20秒，控制强震平稳段的首末时刻分别是5秒和10秒，衰减因子是0.2，则当秒时，地震动时程强度包络函数值是（       ）A． B．1 C．9 D．【答案】A【分析】由题可得当时，，即得.【详解】由题可知，，，∴当时，，∴当秒时，地震动时程强度包络函数值是.故选：A.5．若，，，，则（       ）A． B． C． D．【答案】C【分析】利用基本不等式和对数函数的单调性比较大小即可【详解】 ，又 ，即 ； ， 整理得 ，即 综上， 故选：C6．函数的图像大致为（       ）A． B．C． D．【答案】A【分析】判断函数的奇偶性后排除两个选项，然后考虑函数在原点附近的函数值的正负又排除一个选项，得正确结论．【详解】函数定义域是R，，函数为奇函数，排除BD，时，，排除C．故选：A．7．已知为双曲线的焦点，过作轴的垂线交于点，且，则的渐近线方程是（       ）A． B． C． D．【答案】A【分析】结合通径长得，得出关系求得即得渐近线方程．【详解】因为轴，所以，所以，，，，所以，渐近线方程为．故选：A．8．已知、表示两条不同的直线，表示平面，则下面四个命题正确的是（       ）①若，，则；                    ②若，，则；③若，，则；                    ④若，，则．A．①② B．②③ C．①③ D．③④【答案】D【分析】举例说明判断①②；利用线线、线面垂直的判定、性质推理判断③④作答.【详解】长方体中，平面为平面，直线BC为直线b，如图， 当直线AD为直线a时，满足，，而，①不正确；当直线为直线a时，满足，，而，②不正确；在平面内取两条相交直线m，n，如图，因，则，而，则，又，m，n是相交直线，所以，③正确；因，过直线b作平面，如图， 则有，又，，于是得，从而得，④正确，所以给定命题正确的是③④.故选：D9．已知函数在内单调递增，则在内的零点个数最多为（       ）A．3 B．4 C．5 D．6【答案】B【分析】将 看做整体，对于正弦函数，增区间是 ，则 所对应的的区间必然是增区间的子集，由此可以确定 的最大值.【详解】当 时， ，由于正弦函数的增区间是， ，即 ，解得 ，即 ，又 ，由于 ， ，显然， 越大，周期T越小，零点也越多，故当 时零点最多，当 时， ， ，对应2个周期，故零点数为4；故选：B.10．已知直线和与圆都相切，则圆的面积的最大值是（       ）A． B． C． D．【答案】B【分析】由两平行间距离公式求得圆半径，再表示出圆面积，利用基本不等式、不等式的性质得最大值．【详解】圆半径为，由题意两直线平行，它们间的距离为，，则，显然只有时面积才可以取得最大值．当时，，当且仅当，即时等号成立，故选：B．11．秦九韶是我国南宋数学家，其著作《数书九章》中的大衍求一术、三斜求积术和秦九韶算法是具有世界意义的重要贡献．秦九韶把三角形的三条边分别称为小斜、中斜和大斜，三斜求积术即已知三边长求三角形面积的方法，用公式表示为：，其中，，是的内角，，的对边．已知中，，，则面积的最大值为（       ）A． B． C． D．【答案】A【分析】由正弦定理化进行边角转换可得，代入面积公式，变形后结合二次函数性质得最大值．【详解】由得，，即，所以，，所以，即时，．故选：A．12．已知抛物线的准线交轴于点，过点作直线交于，两点，且，则直线的斜率是（       ）A． B． C． D．【答案】B【分析】首先根据抛物线方程求出准线方程，即可得到的坐标，设直线为，，，联立直线与抛物线方程，消元、列出韦达定理，根据，即可得到，从而求出、，从而求出；【详解】解：抛物线的准线为，所以，设直线为，，，则，即，所以，，因为，即，所以，所以或，所以；故选：B 二、填空题13．若，满足约束条件，则的最大值是________．【答案】2【分析】在坐标平面中画出不等式组对应的可行域，平移动直线后可求目标函数的最大值.【详解】不等式组对应的可行域如图所示：设将动直线平移至处时，有最大值，由可得，故，故答案为：214．已知向量，，则________．【答案】（或-1.5）【分析】利用向量数量积的运算法则可得，即得.【详解】∵向量，，∴，∴.故答案为：.15．在棱长为1的正方体中，点在正方体内切球的球面上运动，点在正方形的内切圆上运动，则线段长度的最大值为________．【答案】【分析】利用正方体的性质可知正方体内切球的球心为正方体的中心，正方形的内切圆为正方形的中心，进而可知线段长度的最大值为，即得.【详解】由正方体的性质可知正方体内切球的球心为正方体的中心，其半径为，正方形的内切圆为正方形的中心，其半径为，由题可知线段长度的最大值为，又，∴线段长度的最大值为.故答案为：.16．已知定义在上的函数满足，且当时，，若的值域为，则实数的取值范围为________．【答案】【分析】由题可得函数关于点对称，进而可得当时，有解，利用基本不等式即得.【详解】∵定义在上的函数满足，∴函数关于点对称，又当时，，要使函数的值域为，则当时，有解，又当时，，当且仅当，即取等号，∴，即实数的取值范围为.故答案为：. 三、解答题17．2022年北京冬奥会开幕式于2月4日在国家体育馆举行，北京成为了历史上首个同时举办夏奥会与冬奥会的“双奥城市”，冬奥会上，各种炫酷的冰雪运动项目在青少年中掀起了一股冰雪运动热潮．为了了解某班学生喜爱冰壶项目是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表： 喜爱冰壶运动不喜爱冰壶运动总计男生 15 女生20  总计  50已知在全班50人中随机抽取1人，抽到喜爱冰壶运动的学生的概率为0.6．(1)请将上面的列联表补充完整（不用写计算过程）；(2)能否在犯错误的概率不超过0.005的前提下认为喜爱冰壶运动与性别有关？附：，其中．0.0250.0100.0050.0015.0246.6357.87910.828【答案】(1)填表见解析(2)能在犯错误的概率不超过0.005的前提下认为喜爱冰壶运动与性别有关【分析】（1）根据题设条件可得完整的列联表.（2）根据公式可求的值，对照临界值表可得相应的结论.【详解】(1)因为喜爱冰壶运动的学生的概率为0.6，故喜爱冰壶运动的学生的人数为30人，故补充完整的列联表如下： 喜爱冰壶运动不喜爱冰壶运动总计男生101525女生20525总计302050(2)由，所以能在犯错误的概率不超过0.005的前提下认为喜爱冰壶运动与性别有关．18．已知首项为1的等差数列的前项和为，若成等比数列．(1)求和：(2)求证：【答案】(1)，(2)证明见解析【分析】（1）设公差为，结合等比数列性质由等差数列基本量法列式求得，得通项公式、前项和公式；（2）由裂项相消法求得不等式左边的和后易证不等式成立．【详解】(1)由题得，设数列的公差为，则，解得或．当时，不符合题意，舍去．所以，．(2)因为时，，所以．19．在棱柱中，底面为平行四边形，为线段上一动点．(1)证明：平面；(2)若平面，，，，且为线段的中点，求点到平面的距离．【答案】(1)证明见解析；(2).【分析】（1）利用线面平行的判定定理及面面平行的判定定理可得平面平面，进而即得；（2）过作于，利用线面垂直的判定及性质可得为到平面的距离，结合条件即求.【详解】(1)连接，．为棱柱，且，∴四边形为平行四边形，，又平面，平面，平面．同理平面，又且，平面，∴平面平面，又平面，平面．(2)如图，在平面内，过作于．，，为正方形．又为中点，．平面，,又，平面，．又，，平面，即为到平面的距离．在中，，边上的高，由等面积可得，，所以到平面的距离为．20．已知椭圆的离心率为，右焦点是，左、右顶点分别是和．直线与椭圆交于，两点，点在轴上方，且当时，．(1)求椭圆的方程；(2)若直线、的斜率分别是和，求的取值范围．【答案】(1)；(2).【分析】（1）由已知及椭圆对称性求参数a，根据离心率及椭圆参数关系即可求解；（2）联立椭圆C和直线方程，应用韦达定理直接计算即可.【详解】(1)由椭圆对称性知： ，即，又，所以，，所以椭圆的方程为；(2)将代入得，设，，则，，由（1）得，，所以，将式代入上式得 ，因为，，所以，即的取值范围是；综上，椭圆C的方程为，的取值范围是.21．已知函数，曲线在处的切线也与曲线相切．(1)求实数的值；(2)求在内的极小值．【答案】(1)；(2)1.【分析】（1）利用导数的几何意义可得切线方程为，然后利用判别式为0即得；（2）令，利用零点存在定理可得存在，使得，然后利用导数可得当时，，当时，，即得.【详解】(1)，，又，所以在处的切线方程为，因为其也与曲线相切，则联立，得，由及，解得．(2)由（1）得，，令，则在上递增，又，．∴存在，使得，即，当时，，递减：当时，，递增，∵，，∴当时，，即．又，当时，，是在内的极小值点．∵当时，递减，即递减，在内没有极小值点．在的极小值是．22．在平面直角坐标系中，以为极点，轴的正半轴为极轴建立极坐标系．已知曲线的极坐标方程为，．(1)直接写出曲线的直角坐标方程，若以为参数，写出曲线的参数方程；(2)若点在曲线上，且点到点的距离为，求点到原点的距离．【答案】(1)；（为参数，）；(2).【分析】（1）利用极坐标与直角坐标互化公式求出曲线的直角坐标方程，再写出其参数方程作答.（2）利用（1）中曲线的参数方程设出点坐标，利用两点间距离公式计算作答.【详解】(1)由曲线的极坐标方程得：，将且代入得：，即，而，，即，曲线的直角坐标方程是，参数方程为（为参数，）.(2)由（1）设点的直角坐标为，，则，化简得，而，则，于是得点，，所以点到原点的距离为．23．已知(1)证明：；(2)已知，，求的最小值，以及取得最小值时的，的值．【答案】(1)证明见解析(2)最小值为， 或【分析】（1）利用作差法证明不等式；（2）令代入（1）中不等式可得最小值及取得最小值是值．【详解】(1)因为，所以，当且仅当时取等号．(2)由（1）可得，所以，即，当且仅当时取等号．由，解得或．综上，的最小值为，此时，的值为或．