
2022年浙江省嘉兴市中考数学考前模拟预测试题(word版含答案)
展开
这是一份2022年浙江省嘉兴市中考数学考前模拟预测试题(word版含答案),共18页。
2022年浙江省嘉兴市中考数学考前模拟预测试题
一.选择题(共10小题,满分30分,每小题3分)
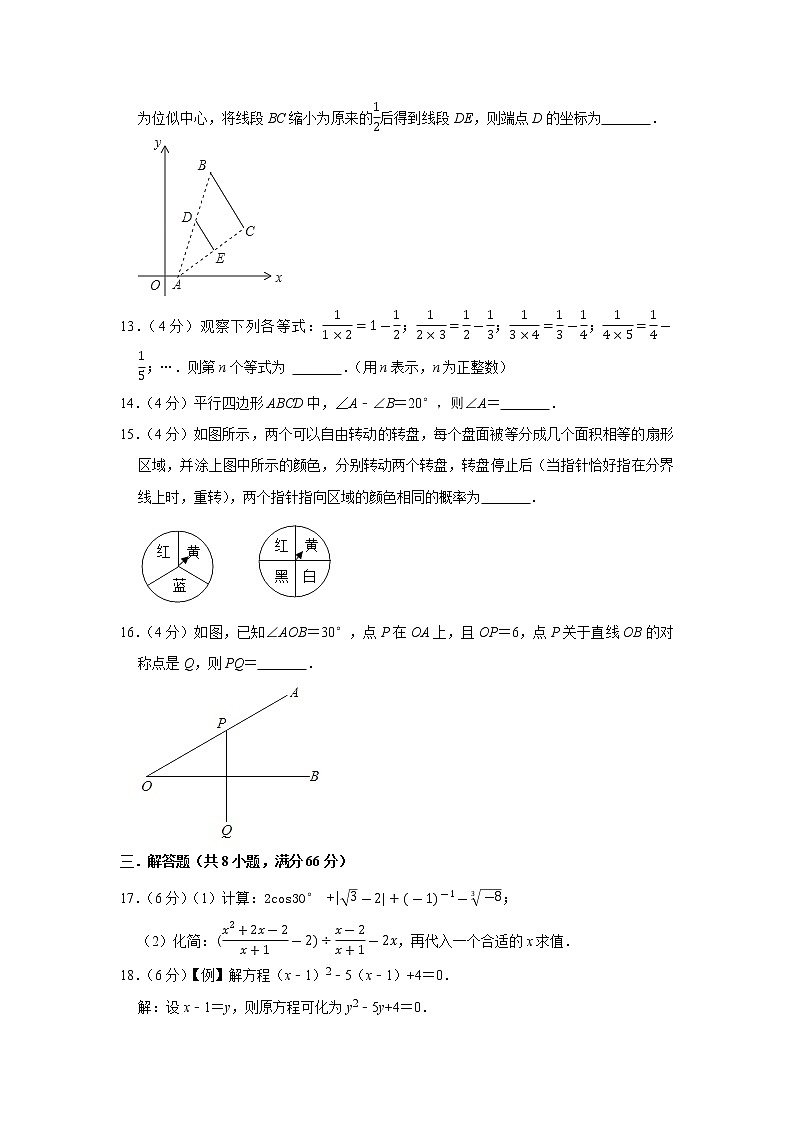
1.(3分)2021年10月16日0时23分我国发射了神舟十三号载人飞船,利用长征二号F运载火箭将神舟十三号载人飞船送入近地点高度200000米的近地轨道,并与天和核心舱进行交会对接.将200000用科学记数法表示应为( )
A.2×104 B.0.2×105 C.20×104 D.2×105
2.(3分)如图是由小立方块搭成的几何体,则从左面看到的几何体的形状图是( )
A. B. C. D.
3.(3分)下列命题中是假命题的是( )
A.两个无理数的和是无理数
B.(﹣10)2的平方根是±10
C.3(-8)2=4
D.平方根等于本身的数是零
4.(3分)若点(﹣1,y1),(2,y2),(3,y3)在反比例函数y=-5x的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y3>y1 C.y3>y1>y2 D.y1>y3>y2
5.(3分)将图1所示的长方形纸片对折后得到图2,图2再对折后得到图3,沿图3中的虚线剪下并展开,所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.梯形
6.(3分)下列说法中正确的是( )
A.数据5,3,3,6,5的众数是3
B.数据2,3,1,0的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣6,﹣5,6的中位数和平均数都是0
7.(3分)若直线l与半径为5的⊙O相离,则圆心O与直线l的距离d为( )
A.d<5 B.d>5 C.d=5 D.d≤5
8.(3分)中秋节是我国的传统节日,人们素有吃月饼的习俗.汾阳月饼不仅汾阳人爱吃,而且风靡省城市场.省城某商场在中秋节来临之际购进A、B两种汾阳月饼共1500个,已知购进A种月饼和B种月饼的费用分别为3000元和2000元,且A种月饼的单价比B种月饼单价多1元.求A、B两种月饼的单价各是多少?设A种月饼单价为x元,根据题意,列方程正确的是( )
A.3000x+2000x+1=1500 B.2000x+3000x+1=1500
C.3000x+2000x-1=1500 D.2000x+3000x-1=1500
9.(3分)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,点E是AC的中点,若DE=5,则AB的长为( )
A.10 B.12 C.13 D.11
10.(3分)已知一次函数y=2x+b(m≤x≤n)的图象经过点P(p,q),下列结论中正确的是( )
A.q﹣b≥2m B.q﹣b≤2m C.q﹣b≥2n D.q+b≥2m
二.填空题(共6小题,满分24分,每小题4分)
11.(4分)关于x,y的方程2x﹣my=﹣4的一组解是:x=-1y=2,则m= .
12.(4分)如图,线段BC的两端点的坐标分别为B(3,8),C(6,3),以点A(1,0)为位似中心,将线段BC缩小为原来的12后得到线段DE,则端点D的坐标为 .
13.(4分)观察下列各等式:11×2=1-12;12×3=12-13;13×4=13-14;14×5=14-15;….则第n个等式为 .(用n表示,n为正整数)
14.(4分)平行四边形ABCD中,∠A﹣∠B=20°,则∠A= .
15.(4分)如图所示,两个可以自由转动的转盘,每个盘面被等分成几个面积相等的扇形区域,并涂上图中所示的颜色,分别转动两个转盘,转盘停止后(当指针恰好指在分界线上时,重转),两个指针指向区域的颜色相同的概率为 .
16.(4分)如图,已知∠AOB=30°,点P在OA上,且OP=6,点P关于直线OB的对称点是Q,则PQ= .
三.解答题(共8小题,满分66分)
17.(6分)(1)计算:2cos30°+|3-2|+(-1)-1-3-8;
(2)化简:(x2+2x-2x+1-2)÷x-2x+1-2x,再代入一个合适的x求值.
18.(6分)【例】解方程(x﹣1)2﹣5(x﹣1)+4=0.
解:设x﹣1=y,则原方程可化为y2﹣5y+4=0.
解得y1=1,y2=4.
当y=1时,即x﹣1=1,解得x=2;
当y=4时,即x﹣1=4,解得x=5.
所以原方程的解为x1=2,x2=5.
上述解法称为“整体换元法”.
(1)请运用“整体换元法”解方程:(2x﹣5)2﹣(2x﹣5)﹣2=0;
(2)已知x2﹣xy﹣y2=0,求xy的值.
19.(6分)小琪同学和爸爸妈妈一起回老家给奶奶过生日,他们为奶奶准备了一个如图所示的正方形蛋糕,蛋糕的每条边上均匀镶嵌着4颗巧克力.爸爸要求小琪只切两刀把蛋糕平均分成4份,使每个人分得的蛋糕和巧克力数都相等.
(1)请你在图1中画出一种分法(无需尺规作图);
(2)如图2,小琪同学过正方形的中心切了一刀,请你用尺规作图帮她作出第2刀所在的直线.(不写作法,保留作图痕迹)
20.(8分)根据数学家凯勒的“百米赛跑数学模型”,前30米称为“加速期”,30米~80米为“中途期”,80米~100米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(m/s)与路程x(m)之间的观测数据,绘制成曲线如图所示.
(1)y是关于x的函数吗?为什么?
(2)“中途期”结束时,小斌的速度为多少?
(3)根据如图提供的信息,给小斌提一条训练建议.
21.(8分)球类运动是同学们非常喜欢的日常体育运动,为了更合理地配置体育运动器材和场地,某校针对“你最喜爱的球类运动”进行了一次随机抽样调查(每名被调查者分别选一项球类运动),并把调查结果绘制成如图所示的两个统计图表(不完整).
某校学生最喜爱的球类运动统计表
最喜爱的球类运动
人数
足球
27
篮球
a
乒乓球
24
羽毛球
24
排球
b
请根据所给信息,解答下列问题:
(1)本次被抽样调查的学生共有多少人?
(2)求扇形统计图中最喜爱篮球部分的圆心角度数;
(3)若该校共有学生960人,请根据抽样结果估计学生中最喜爱乒乓球或排球的人数.
22.(10分)如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.
(1)如图①,小明通过按压点A打开杯盖AD注入热水(点D,D′为对应点).若∠DAD′=120°,求点D的运动路径长.
(2)如图②,将茶杯支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出,求此时杯子最高点A距离桌面的距离.(参考数据sin53°≈0.8,cos53°≈0.6)
23.(10分)如图,已知二次函数y=x2+ax+a+1的图象经过点P(﹣2,3).
(1)求a的值和图象的顶点坐标;
(2)点Q(m,n)在该二次函数图象上;
①当n=11时,求m的值.
②当m≤x≤m+3时,该二次函数有最小值11,请直接写出m的值.
24.(12分)如图,在菱形ABCD中,∠ABC=60°,经过点A的直线(不与BD垂直)与对角线BD所在直线交于点E,过点B,D分别作直线BD的垂线交直线AE于点F,H.
(1)当点E在如图①位置时,求证:BF﹣DH=33BD;(提示:延长DA交BF于G)
(2)当点E在图②、图③的位置时,直接写出线段BF,DH,BD之间的数量关系,不需要证明;
(3)在(1)、(2)的条件下,若DH=1,BD=43,则tan∠DHE= .
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:200000=2×105.
故选:D.
2.【解答】解:从左面正投影所得到的图形为选项B.
故选:B.
3.【解答】解:A、-2+2=0,0不是无理数,
∴两个无理数的和是无理数,是假命题;
B、(﹣10)2=100,100的平方根是±10,
∴(﹣10)2的平方根是±10,是真命题;
C、3(-8)2=364=4,本选项说法是真命题;
D、平方根等于本身的数是零,是真命题;
故选:A.
4.【解答】解:∵k=﹣5<0,
∴在每个象限内,y随x值的增大而增大,
∴当x=﹣1时,y1>0,
∵2<3,
∴y2<y3<y1
故选:D.
5.【解答】解:展开图如图所示,它是菱形.理由如下:
由操作过程可知OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵OA⊥OB,
即AC⊥BD,
∴四边形ABCD是菱形.
故选:B.
6.【解答】解:A、数据5,3,3,6,5中数据3和5出现的次数相同且最多,故众数为3和5,故本选项错误;
B、数据2,3,1,0排序后为0、1、2、3,故中位数为(1+2)÷2=1.5,故本选项错误;
C、当一组数据的每个数据相等时,其众数及中位数相等,故本选项错误;
D、数据0、5、﹣6、﹣5、6的中位数为0,平均数为0,故本选项正确.
故选:D.
7.【解答】解:∵直线l与⊙O的位置关系是相离,
∴d>r,
∴r=5,
∴d>5,
故选:B.
8.【解答】解:设A种月饼单价为x元,根据题意,得3000x+2000x-1=1500.
故选:C.
9.【解答】解:∵AB=AC,AD⊥BC,
∴CD=DB,
∵CE=EA,
∴AB=2DE=10,
故选:A.
10.【解答】解:∵一次函数y=2x+b(m≤x≤n)的图象经过点P(p,q),
∴q=2p+b,
∴q﹣b=2p.
又∵p≥m,
∴q﹣b≥2m.
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.【解答】解:把x=-1y=2代入方程2x﹣my=﹣4得:﹣2﹣2m=﹣4,
解得:m=1,
故答案为:1.
12.【解答】解:∵将线段BC缩小为原来的12后得到线段DE,
∴△ADE∽△ABC,
∴ADAB=DEBC=12,
∴点D是线段AB的中点,
∵A(1,0),B(3,8),
∴点D的坐标为(2,4),
故答案为:(2,4).
13.【解答】解:∵11×2=1-12,12×3=12-13,13×4=13-14,14×5=14-15,…,
∴第n个式子是:1n(n+1)=1n-1n+1,
故答案为:1n(n+1)=1n-1n+1.
14.【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
又∵∠A﹣∠B=20°,
∴∠A=100°,∠B=80°.
故答案为100°.
15.【解答】解:根据题意画出树状图如下:
根据树状图可知:所有等可能的结果有12种,其中颜色相同的有2种,
∴两个指针指向区域的颜色相同的概率为:212=16,
故答案为:16.
16.【解答】解:如图,连OQ,
∵点P关于直线OB的对称点是Q,
∴OB垂直平分PQ,
∴∠POB=∠QOB=30°,OP=OQ,
∴∠POQ=60°,
∴△POQ为等边三角形,
∴PQ=PO=6.
故答案为6.
三.解答题(共8小题,满分66分)
17.【解答】解:(1)原式=2×32+2-3+(﹣1)﹣(﹣2)
=3+2-3-1+2
=3;
(2)原式=[x2+2x-2x+1-2(x+1)x+1]•x+1x-2-2x
=x2+2x-2-2x-2x+1•x+1x-2-2x
=x2-4x+1•x+1x-2-2x
=(x+2)(x-2)x+1•x+1x-2-2x
=x+2﹣2x
=2﹣x,
∵x+1≠0且x﹣2≠0,
∴x≠﹣1且x≠2,
当x=1时,
原式=2﹣1=1.
18.【解答】解:(1)设y=2x﹣5,则原方程变形为y2﹣y﹣2=0,
解得y1=2,y2=﹣1,
当y=2时,即2x﹣5=2,解得x=3.5;
当y=﹣1时,2x﹣5=﹣1,解得x=2.
所以原方程的解为x1=3.5,x2=2;
(2)x2﹣xy﹣y2=0,
方程两边同时除以y2,得x2-xy-y2y2=0,
设xy=m,方程可化为m2﹣m﹣1=0,
解得m1=1+52,m2=1-52,
∴xy的值为1+52或1-52.
19.【解答】解:(1)如图,直线a,直线b即为所求.
(2)如图,直线c即为所求.
20.【解答】解:(1)y是关于x的函数,
理由:对于自变量x的每一个值,y都有唯一的值与它对应;
(2)“中途期”结束时,小斌的速度为:10.7m/s;
(3)由图可知,小斌在80米左右时速度下降明显,建议增加耐力训练,提高成绩.
21.【解答】解:(1)27÷22.5%=120人,
答:次被抽样调查的学生共有120人,
(2)120×12.5%=15人,即b=15,a=120﹣15﹣24﹣24﹣27=30人,
360°×30120=90°,
答:扇形统计图中最喜爱篮球部分的圆心角度数为90°,
(3)960×24+15120=312人,
答:该校960名学生中最喜爱乒乓球或排球的有312人.
22.【解答】解:(1)点D的运动路径长为 120×π×15180=10πcm,
∴点D的运动路径长为10πcm;
(2)如图,过点D作DG⊥CG于G,过点A作AF⊥DG于F,
由题意可知,∠FAD=∠GDC=∠BCH=53°,
∵AD=15cm,DC=20cm,
∴sin53°=FD15≈0.8,cos53°=DG20≈0.6,
∴FD=12cm,DG=12cm,
∴FG=24cm,
∴此时杯子最高点A距离桌面的距离为24cm.
23.【解答】解:(1)∵二次函数y=x2+ax+a+1的图象经过点P(﹣2,3),
∴3=(﹣2)2+a×(﹣2)+a+1,
解得a=2,
∴y=x2+2x+3=(x+1)2+2,
∴该函数图象的顶点坐标是(﹣1,2);
(2)①∵点Q(m,n)在该二次函数图象上,n=11,
∴11=m2+2m+3,
解得m=﹣4或2;
②∵y=x2+2x+3=(x+1)2+2,
∴该函数图象开口向上,当x=﹣1时取得最小值2,
∵当m≤x≤m+3时,该二次函数有最小值11,
∴当m>﹣1时,m2+2m+3=11,得m1=﹣4(舍去),m2=2;
当m<﹣1<m+3时,该函数的最小值为2,不符合题意;
当m+3<﹣1时,(m+3)2+2(m+3)+3=11,得m3=﹣1(舍去),m4=﹣7;
由上可得,m的值是2或﹣7.
24.【解答】(1)证明:延长DA交BF于G,如图①所示:
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,BD平分∠ABC,
∴∠GAB=∠ABC=60°,∠ABD=∠ADB=12∠ABC=30°,
∵FB⊥BD,DH⊥BD,
∴∠FBD=∠HDB=90°,
∴FB∥DH,∠GBA=90°﹣∠ABD=60°,
∴△ABG是等边三角形,
∴AG=AB=AD,
∵FB∥DH,
∴∠FGA=∠ADH,∠BFA=∠AHD,
∴△FGA≌△HDA(AAS),
∴FG=DH,
∴BF﹣DH=BF﹣FG=BG,
在Rt△BDG中,tan∠GDB=BGBD,
∴BG=BD×tan∠GDB=BD×tan30°=33BD,
∴BF﹣DH=33BD;
(2)如图②中,结论:DH﹣BF=33BD,理由如下:
延长BA交DH于G,
同①得:△ADG是等边三角形,△HGA≌△FBA(AAS),
∴AG=DG=AD,GH=BF,
∴DH﹣BF=DH﹣GH=DG,
在Rt△BDG中,tan∠GBD=DGBD,
∴DG=BD×tan∠GBD=BD×tan30°=33BD,
∴DH﹣BF=33BD;
如图③中,结论:BF+DH=33BD,理由如下:
延长DA交BF的延长线于G,
同①得:△ABG是等边三角形,△FGA≌△HDA(AAS),
∴AG=BG=AD,GF=DH,
∴BF+DH=BF+GF=BG,
在Rt△BDG中,tan∠GDB=BGBD,
∴BG=BD×tan∠GDB=BD×tan30°=33BD,
∴BF+DH=33BD;
(3)分两种情况:
a、如图①﹣1中,延长DA交BF于G,连接AC交BD于O,
由(1)得:BF﹣DH=33BD,
∴BF﹣1=33×43=4,
∴BF=5,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD,OA=OC,OB=OD=12BD=23,∠ABD=∠ADB=12∠ABC=30°,
∴OA=33OD=2,
∵FB⊥BD,
∴FB∥AC,
∴△AOE∽△FBE,
∴OABF=OEBE,
即25=23-DE43-DE,
解得:DE=233,
∵DH=1,
∴tan∠DHE=DEDH=233;
b、如图③﹣1中,延长DA交BF的延长线于G,连接AC交BD于O,
由(2)得:BF+DH=33BD,
即BF+1=33×43=4,
∴BF=3,
同上得:△AOE∽△FBE,
∴OABF=OEBE,
即23=23+DE43+DE,
解得:DE=23,
∵DH=1,
∴tan∠DHE=DEDH=23;
综上所述,tan∠DHE的值为233或23,
故答案为:233或23
相关试卷
这是一份2022年浙江省嘉兴市中考数学考前模拟预测试题,共17页。
这是一份2022年江苏省苏州市中考数学考前模拟预测试题 (word版含答案),共23页。试卷主要包含了万亿元等内容,欢迎下载使用。
这是一份2022年湖南省长沙市中考数学考前冲刺模拟预测卷(word版含答案),共18页。









