2022年浙江省宁波市北仑区初中学业水平模拟考试数学试卷（附答案）

 初中学业水平模拟考试数学试卷

一、选择题 (本大题共10小题, 每小题4分, 共40分.)

1．-5 的绝对值是(　　)

A．-5 B． C．5 D．

2． 接种新冠疫苗不仅可以预防新冠病毒感染， 也可以顶防重症， 降低死亡率. 经统计， 北仑区到2022年2月份为止已有约81万人完成新冠疫苗接种. 其中81万人用科学记数法可表示为(　　)

A．人 B．人 C．人 D．人

3．要使代数式有意义，的取值应满足(　　)

A． B． C． D．

4．下列计算正确的是(　　)

A． B．

C． D．

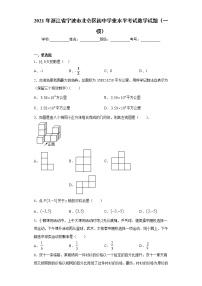
5．由5个相同的立方体搭成的几何体如图所示， 则它的主视图是(　　)

A． B．

C． D．

6．某校食堂每天为学生提供A， B两种套餐，如果甲，乙两人同去该食堂就餐，那么甲，乙两人选择同套餐的概率为(　　)

A． B． C． D．

7．在四边形中， ，点是对角线的中点， 则 的长为(　　)

A． B． C．6 D．5

8．如图， 是的直径， C、D是上的点， ， 过点作的切线交 的延长线于点，则的值为(　　)

A． B． C． D．

9．如图，直线与反比例函数 的图象交于A、B两点， 过点作交轴于点，若的面积为5， 则的值为(　　)

A．2 B．4 C．5 D．8

10．用面积为的四张长方形纸片拼成如图所示的一个大长方形， 则图中阴影的面积为(　　)

A． B． C． D．

二、填空题（每小题5分, 共30分)

11．分解因式： 4x2-100=　                　.

12．如图，将线段绕点顺时针旋转， 得到线段， 若， 则点经过的路径的长度为　     　.

13． 方程的解为　     　.

14． 北仑梅山所产的草莓柔嫩多汁，芳香味美，深受消费者喜爱。有一草莓种植大户，每天草莓的采摘量为300千克，当草莓的零售价为22元/千克时，刚好可以全部售完。经调查发现，零售价每上涨1元，每天的销量就减少30千克，而剩余的草莓可由批发商以18元/千克的价格统一收购走，则当草莓零售价为　     　元时，该种植户一天的销售收入最大。

15．如图， 在梯形 中， ， ， 以 为直径作 ， 恰与 相切于点 ， 连结 ， 若梯形 的面积是 与 的长度和为13 ， 则 的长为　     　.

16．如图， 在矩形 中， ， 点 是 的中点， 点 是对角线 上一动点， ， 连结 ， 作点 关于直线 的对称点 ， 直线 交 于点 ， 当 是直角三角形吋， 的长为　           　.

三、解答题

17．  

（1）计算：

（2）解不等式组：

18．如图，在边长为1的正方形网格内，点A、B、C、 D均在格点处， 移动点A、B、C、 D的其中一点，使这点仍落在格点处，把原四边形变形成一个与它面积相等的三角形或平行四边形.

（1）变形成三角形，

（2）变形成平行四边形(非矩形)

19． 如图，抛物线经过点和点.

（1）求抛物线的解析式；

（2）若将上述抛物线向右平移个单位， 此时点平移到点， 点平移到点， 连接 ， 若四边形是菱形， 求平移后抛物线的解析式.

20．2021年， 中国航天人在太空又书写了新的奇迹. 为增进学生对航天知识的了解， 某校开展了相关的宜传教育活动. 现随机抽取部分学生进行航天知识竟赛活动， 并将所得数据绘制成如下不完整的条形统计图和扇形统计图.

根据以上信息， 回答下列问题：

（1）本次抽样的样本容量为　     　，“良好"所在扇形的圆心角的度数是　     　.

（2） 补全条形统计图

（3） 若该校共有学生1500人， 估计该校学生在这次竞赛中获得良好及以上的学生有多少人?

21．某镇为创建特色小镇， 助力乡村振兴， 决定在辖区的一条河上修建一座步行观光桥. 如图， 该河旁有一座小山，山高， 坡面的坡比为 (注： 坡比是指坡面的铅垂高度与水平宽度的比)， 点C， 与河岸在同一水平线上， 从山顶处测得河岸和对岸的俯角分别为.

(参考数据： ， )

（1）求山脚到河岸的距离；

（2）若在此处建桥， 试求河宽EF的长度. (结果精确到)

22．甲、乙两地间的直线公路长为600千米， 一辆轿车与一辆货车分别沿该公路从甲、乙两地以各自的速度相向而行， 货车比轿车早出发1小时， 途中轿车出现了故障， 停下维修， 货车仍继续行驶。1小时后轿车故障被排除，此时接到通知，轿车立刻掉头按原路原速返回甲地（接到通知及掉头时间不计）最后两车同时到达甲地， 已知两车距各自出发地的距离 (千米)与轿车所用的时间 (小时) 的关系如图所示，请结合图象解答下列问题：

如图所示， 请结合图像解答下列问题：

（1）货车的速度是　     　千米/时， 的值是　     　，轿车的速度是　     　千米/时；

（2） 求轿车距其出发地的距离 (千米)与所用时间 (小时)之间函数表达式；

（3） 求货车出发多长时间两车相距120千米.

23．如图

（1） 【根底巩固】

如图， 在中， 为上一点， . 求证： .

（2） 【尝试应用】

如图2， 在菱形中， 分别为上的点， 且， 射线 交的延长线与点， 射线交的延长线于点. 若. .

求： ①CM的长；

②FN的长.

（3）【拓展进步】

如图3，在菱形中， ， 以点为圆心作半径为3的圆， 其中点 是圆上的动点， 请直接写出的最小值.

24．有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.

（1）如图1， 在等邻边互补四边形中， ， 且， 则　     　.

（2）如图2， 在等邻边互补四边形中， ， 且， 求证：

（3）如图3， 四边形内接于， 连结并延长分别交于点， 交 于点， 若点是的中点， ， 求的长.

答案解析部分

1．【答案】C

2．【答案】C

3．【答案】B

4．【答案】B

5．【答案】D

6．【答案】A

7．【答案】B

8．【答案】D

9．【答案】D

10．【答案】A

11．【答案】4（x+5）（x-5）

12．【答案】

13．【答案】x=-5

14．【答案】25

15．【答案】11

16．【答案】1或3或3-

17．【答案】（1）解：原式=4x2-4x+1-1+4x2
=8x2-4x；

（2）解：，
解不等式①得，x≤1，
解不等式②得，x＞-4，
∴不等式组的解集为-4＜x≤1.

18．【答案】（1）解：如图，
 

（2）解：如图，

19．【答案】（1）解：将点A（-4，0）和点B（0，3）代入y=mx2+mx+n中，
得，
解得，
∴y=-x2-x+3；

（2）解：如图所示，

∵A（-4，0）、B（0，3），
∴OA=4，OB=3，
由勾股定理得，AB=5，
∵四边形ABCD是菱形，
∴AD=AB=5，
∴a=5，
∵y=-x2-x+3=-（x+）2+，
∴向右平移5个单位后，函数解析式为y=-（x-）2+，
整理得：y=-x2+x-.

20．【答案】（1）60；144º

（2）解：合格人数为：60-24-15-9=12（人），
∴补全条形图如下：
 

（3）解：×1500=975（人），
∴估计该校学生在这次竞赛中获得良好及以上的学生有975人．

21．【答案】（1）解：由题意得：
BC=100m，BC：AC=1：0.7，
∴AC=0.7BC=70m，
∵BD∥CF，∠DBE=45°，
∴∠BEC=45°，
在Rt△BCE中，∠BEC=45°，
∴CE=BC=100m，
∴AE=CE-AC=100-70=30m，
∴山脚A到河岸E的距离为30m；

（2）解：BD∥CF，∠DBF=28°，
∴∠BFC＝28°，
∴在Rt△BCF中，CF==≈188.68m，
∴EF=CF-CE=188.68-100≈88.7m，
∴河宽EF的长度为88.7m．

22．【答案】（1）60；4；90

（2）解：由题意可知：B（5，360），C（9，0），
设直线BC的解析式为y=kx+b（k≠0），
把B（5，360），C（9，0）代入得：，
解得 ，
∴y=﹣80x+560；

（3）解：设货车出发a小时后两车相距120km，
当0＜a≤4时，60a+90（a-1）=600﹣120，解得a=3.8，符合；
当4＜a≤5时，90×4+60a-600=120，解得a=6，不符合，舍去；
当5＜a≤9时，当a=6时，货车行驶距离为6×60=360km，轿车行驶距离为（6-1-1）×90=360km，
∴轿车与货车相距距离=360+360-600=120km，
综上所述，当a=3.8或6时，两车相距120km.

23．【答案】（1）证明：∵∠ACD=∠B，∠A=∠A，
∴△ADC∽△ACB，
∴，
∴AC2=AD·AB； 

（2）解：①如图，连接AC，

∵四边形ABCD是菱形，
∴AB∥CD，∠BAC=∠BAD，
∴∠BAE=∠CME，
又∵∠EAF=∠BAD，
∴∠CME=∠CAF，
又∵∠CFA=∠AFM，
∴△CFA∽△AFM，
∴，
∴AF2=CF·MF，
∵AF=4，CF=2，
∴MF=8，
∴CM=MF-CF=8-2=6；
②由△CFA∽△AFM，可得，即，解得AC=5，
∵四边形ABCD是菱形，
∴AB∥CD，∠BCA=∠DCA，
∴∠BAE=∠CME，∠MCA=∠ACN，
又由①可知：∠CME=∠CAF，
∴△MCA∽△ACN，
∴，
∴
∴AN=，
∴FN=AN-AF=-4=； 

（3）解：解：如图，连接PB，在BC上截取BE，使得BE=BP=，并连接PE，

∵菱形ABCD，AB=6，圆B的半径为3，
∴BP=BC=3，
又∵∠PBE=∠CBP，
∴△PBE∽△CBP，
∴PE=PC，
∴PD+PC=PD+PE，
∴当P、D、E三点共线时，PD+PE最小，最小为ED，
∴PD+PC的最小值为ED的长，
连接DE，过点D作DF⊥BC的延长线于点F，
∵∠ABC=60°，
∴∠DCF=60°，
∴CF=3，DF=3，
∴EF=EC+CF=6-+3=，
∴ED==，
∴PD+PC的最小值为. 

24．【答案】（1）60°

（2）证明：如图2中，延长AB到E，使BE=AD，连接CE，

∵∠BAD=90°，∠BAD+∠BCD=180°，
∴∠BCD=90°，
∵∠D+∠ABC=180°，∠CBE+∠ABC=180°，
∴∠D=∠CBE，
又∵BC=CD
∴△ADC≌△EBC（SAS），
∴AC=EC，∠BCE=∠ACD，
∴∠ACE=∠BCE+∠ACB=∠ACD+∠ACB=∠BCD＝90°，
∴AE2=（AB+BE）2=AC2+EC2，
即（AB+AD）2＝2AC2，
∵AB、AD、AC均为正数，
∴AB+AD＝AC； 

（3）解：如图3中，连接OA，OC，AG，CG，作FH⊥CG于H，

∵点E是AC的中点，AC=6，
∴AE=EC=3，
∴OD⊥AC， ，
∴∠AOE=∠COE，GA＝GC，
∴∠AGF=∠CGF，
∵∠AOC=2∠ABC，
∴∠AOE=∠ABC，
∴tan∠AOE=tan∠ABC==，
∴OE=，
∴OA=，
∴GD=2OA=，DE=OD-OE=，GE=OG+OE=4，
∴AD=，
∵DG是⊙O的直径，
∴∠GAD=90°，
∴GA＝GC==5，
∵，
∴∠ACB=∠BCG，
∵∠AGF=∠CGF，
∴点F是△AGC的内心，
设FM=FE=d，
∵S△ACG=（AC+GA+GC）•d=AC•EG，即（6+5+5）·d=6×4，
∴d=，
∴EF=，
∴FG=EG-EF=4-=.