数学八年级上册第十二章 全等三角形综合与测试多媒体教学ppt课件

专题12.1 探究全等三角形的常见模型

学校:___________姓名：___________班级：___________考号：___________

【模型1】 “一线三直角”模型

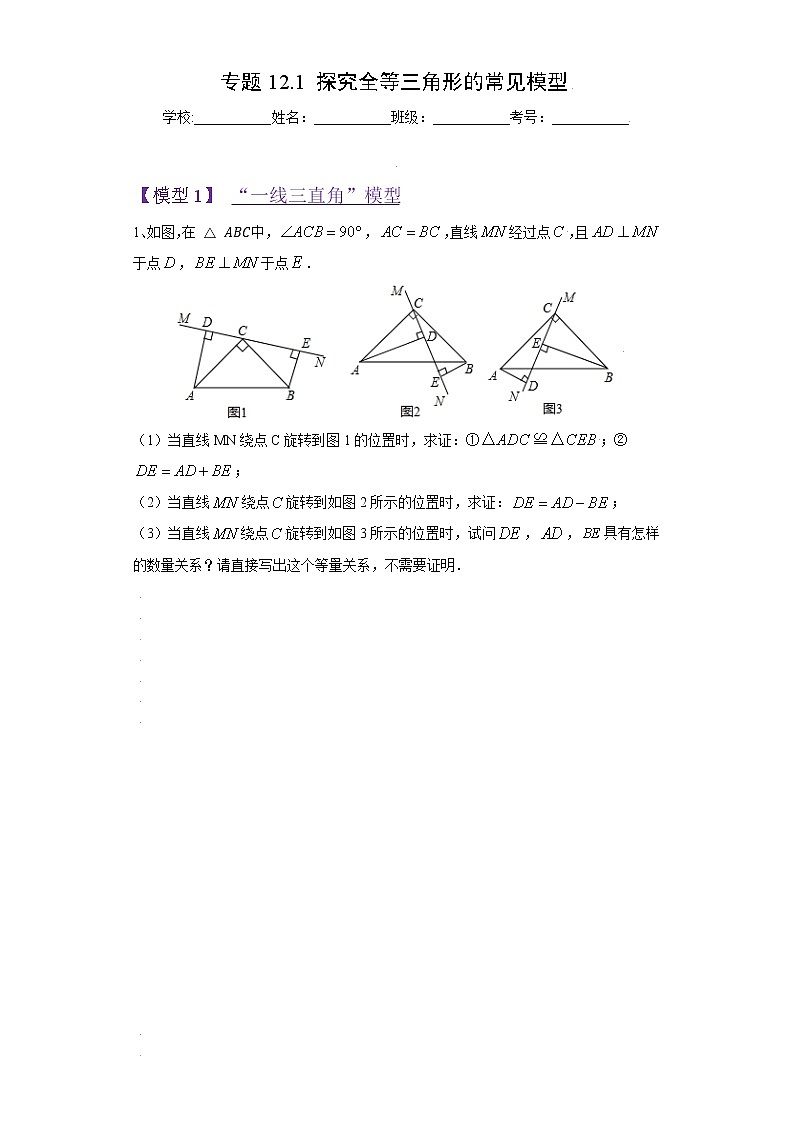
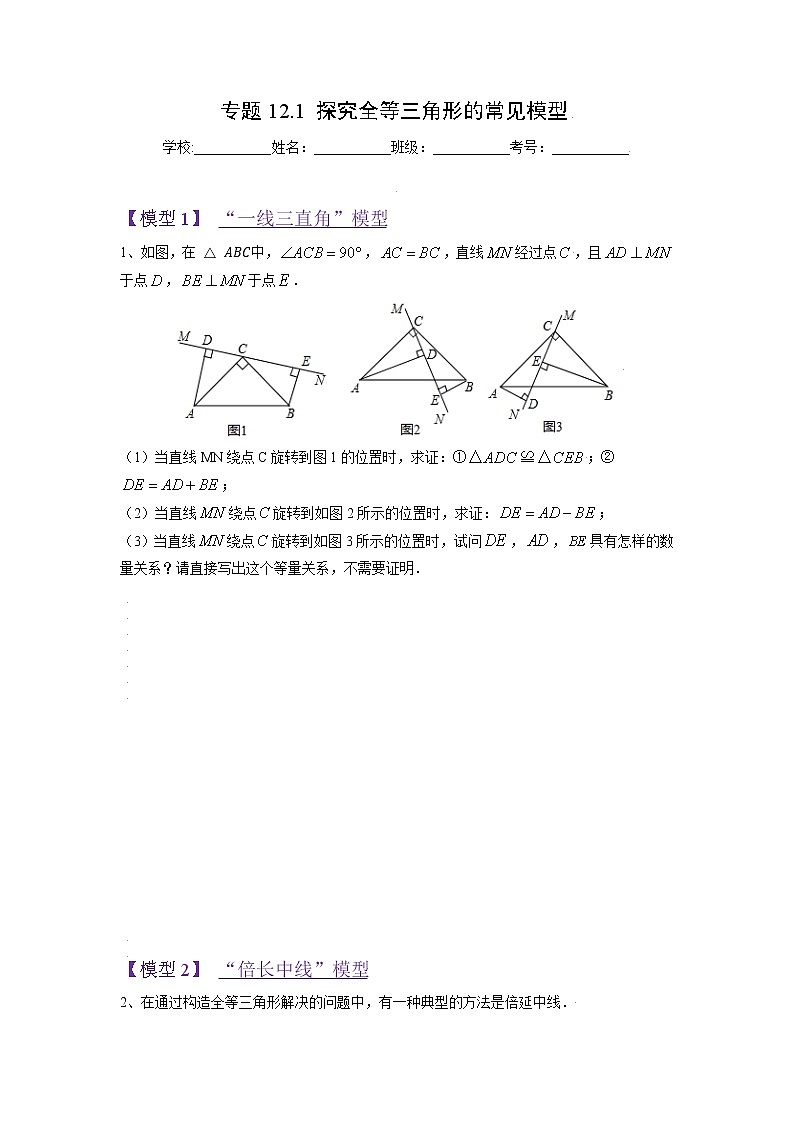
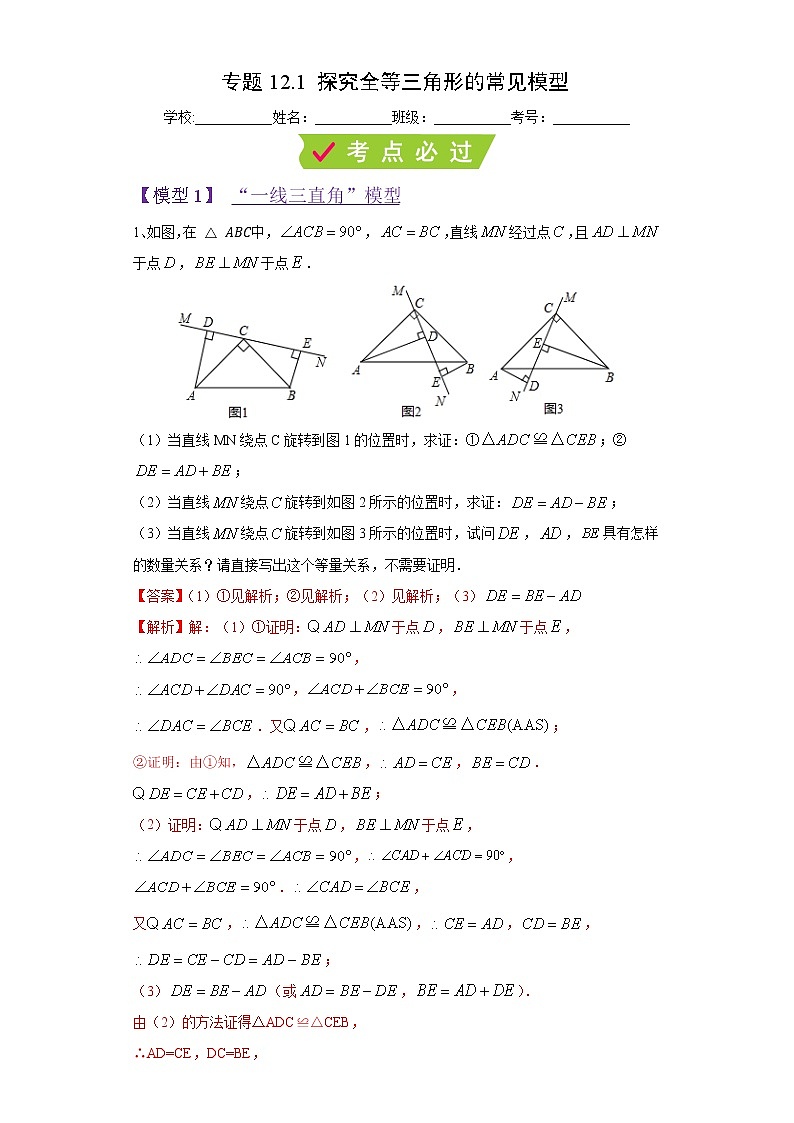
1、如图，在中，，，直线经过点，且于点，于点．

（1）当直线MN绕点C旋转到图1的位置时，求证：①；②；

（2）当直线绕点旋转到如图2所示的位置时，求证：；

（3）当直线绕点旋转到如图3所示的位置时，试问，，具有怎样的数量关系？请直接写出这个等量关系，不需要证明．

【答案】（1）①见解析；②见解析；（2）见解析；（3）

【解析】解：（1）①证明：于点，于点，，

，，

．又，；

②证明：由①知，，，．

，；

（2）证明：于点，于点，

，，．，

又，，，，

；

（3）（或，）．

由（2）的方法证得△ADC≌△CEB，
∴AD=CE，DC=BE，
∴DE=CDCE=BEAD．

【模型2】 “倍长中线”模型

2、在通过构造全等三角形解决的问题中，有一种典型的方法是倍延中线．

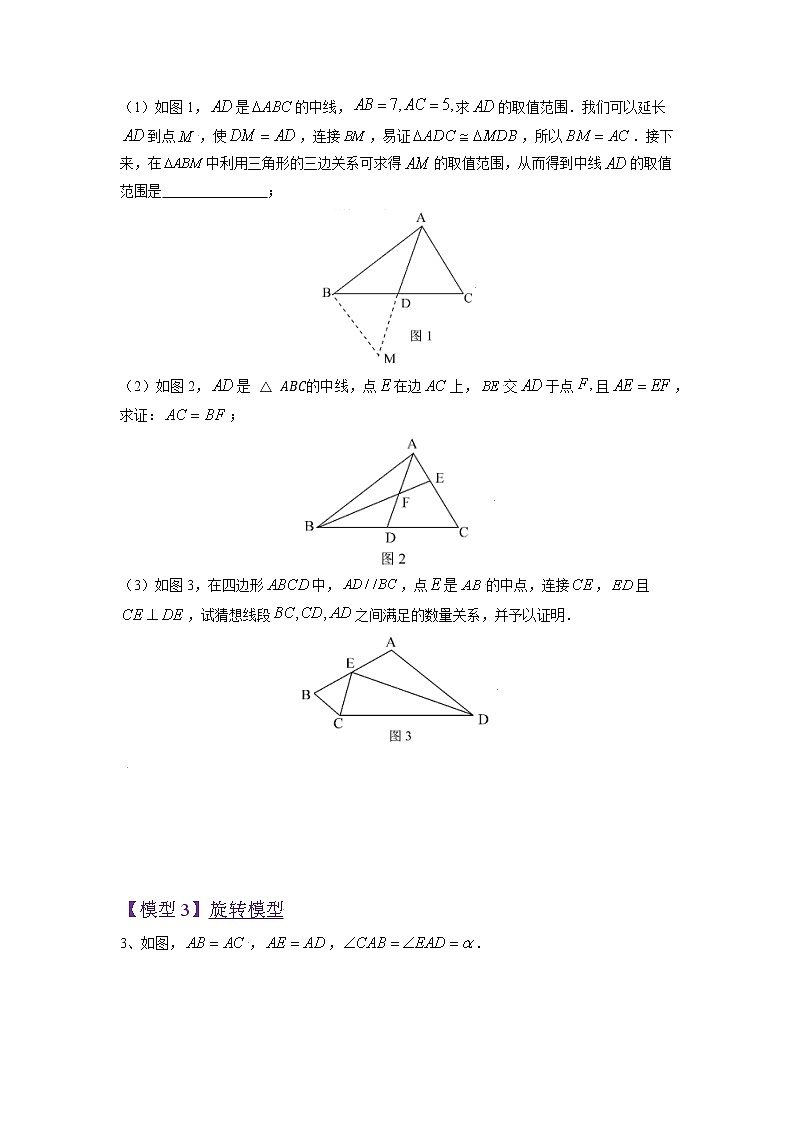
（1）如图1，是的中线，求的取值范围．我们可以延长到点，使，连接，易证，所以．接下来，在中利用三角形的三边关系可求得的取值范围，从而得到中线的取值范围是               ；

（2）如图2，是的中线，点在边上，交于点且，求证：；

（3）如图3，在四边形中，，点是的中点，连接，且，试猜想线段之间满足的数量关系，并予以证明．

【答案】（1）；（2）见解析；（3），证明见解析

【解析】（1）延长到点，使，连接，

∵是的中线，∴，

在和中，，，，

∴，∴，

在中，，

∴，即，∴；

（2）证明:延长到点使,连接，

由（1）知，

∴，

，，

，，

，，，

（3），

延长到，使，连接，

，

，

，，，

点在一条直线上，

，∴，

∴在和中，

，，，

∴≌，，

∵，．

【模型3】旋转模型

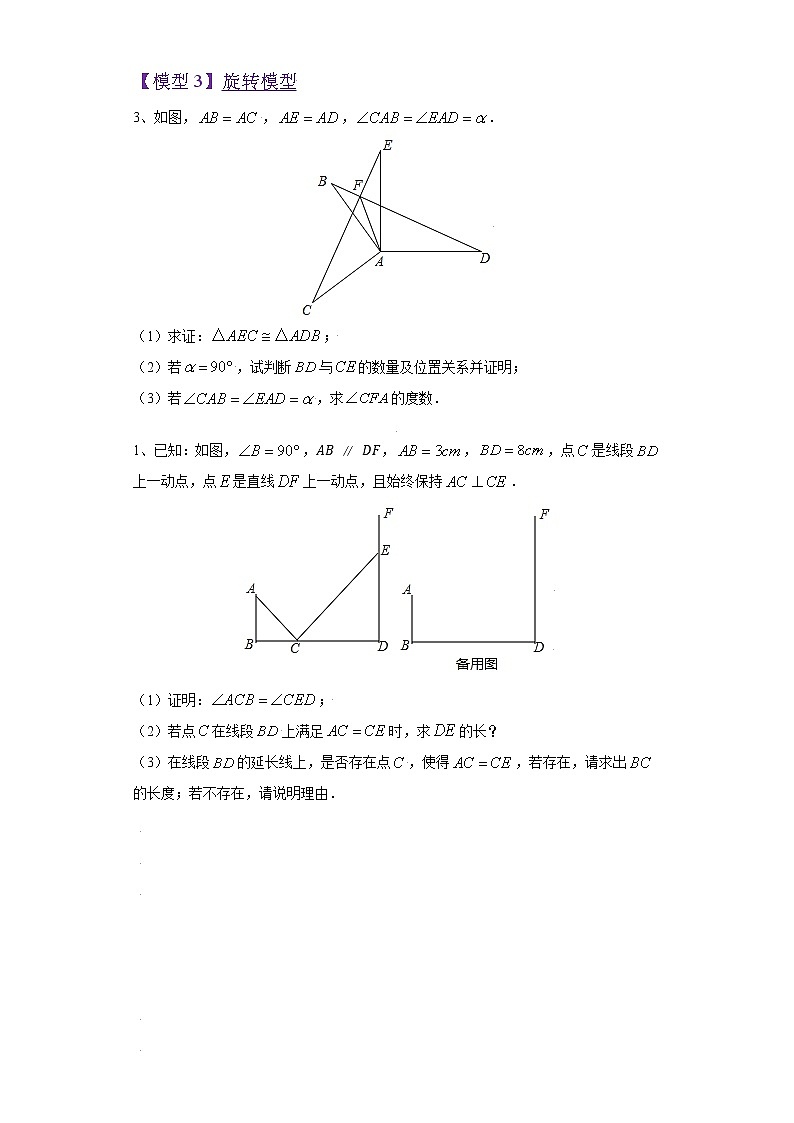
3、如图，，，．

（1）求证：；

（2）若，试判断与的数量及位置关系并证明；

（3）若，求的度数．

【答案】（1）见详解；（2）BD=CE，BD⊥CE；（3）

【解析】（1）∵∠CAB=∠EAD∴∠CAB+∠BAE=∠EAD+∠BAE，

∴ ∠CAE=∠BAD，

∵AB=AC，AE=AD在△AEC和△ADB中∴ △AEC≌△ADB（SAS）

（2）CE=BD且CE⊥BD，证明如下：

将直线CE与AB的交点记为点O，

由（1）可知△AEC≌△ADB，∴ CE=BD， ∠ACE=∠ABD，

∵∠BOF=∠AOC，∠=90°，∴ ∠BFO=∠CAB=∠=90°，∴ CE⊥BD．

（3）过A分别做AM⊥CE，AN⊥BD

由（1）知△AEC≌△ADB，∴两个三角形面积相等

故AM·CE=AN·BD∴AM=AN∴AF平分∠DFC

由（2）可知∠BFC=∠BAC=

∴∠DFC=180°-∴∠CFA=∠DFC=

1、已知：如图，，，，，点是线段上一动点，点是直线上一动点，且始终保持．

（1）证明：；

（2）若点在线段上满足时，求的长？

（3）在线段的延长线上，是否存在点，使得，若存在，请求出的长度；若不存在，请说明理由．

【答案】（1）见解析；（2）5cm；（3）存在，11cm

【解析】解：（1）∵，，∴，

∵，∴，

∴，，

∴

（2）∵在和中

∴，∴，

∴

（3）存在，理由如下：

∵，，∴，

∵，∴，

∴，，∴；

∵在和中

∴，、∴，

∵，BD=8cm

∴．

2、如图，在△ABC中，∠ACB＝90°，AC＝BC，点E是∠ACB内部一点，连接CE，作AD⊥CE，BE⊥CE，垂足分别为点D，E．

（1）求证：△BCE≌△CAD；

（2）请直接写出AD，BE，DE之间的数量关系：　   　．

【答案】（1）见解析；（2）AD＝BE+DE

【解析】证明：（1）∵BE⊥CE，AD⊥CE，

∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．

∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA，

在△BCE和△CAD中，

，∴△BCE≌△CAD（AAS）；

（2）∵△BCE≌△CAD，

∴BE＝DC，AD＝CE，∴AD＝CE＝CD+DE＝BE+DE，

故答案为：AD＝BE+DE．

3、如图，等边△ABC的边长为6，点P从点B出发沿射线BA移动，同时，点Q从点C出发沿线段AC的延长线移动，已知点P、Q移动的速度相同，PQ与直线BC相交于点D.

（1）如图①，当点P为AB的中点时，求CD的长；

（2）如图②，过点P作直线BC的垂线，垂足为E，当点P、Q在移动的过程中，线段BE、DE、CD中是否存在长度保持不变的线段？请说明理由.

【答案】（1）；（2）线段ED的长度保持不变.

【解析】解：（1）如图，过P点作PF∥AC交BC于F，

∵点P和点Q同时出发，且速度相同，

∴BP=CQ，

∵PF∥AQ，∴∠PFB=∠ACB=60°，∠DPF=∠CQD，

又∵AB=AC，∴∠B=∠ACB，∴∠B=∠PFB，∴BP=PF，

∴PF=CQ，又∠PDF=∠QDC，

∴△PFD≌△QCD，且△PBF是等边三角形

∴，BF=PB

∵P是AB的中点，即，

∴BF=3∴;

（2）分两种情况讨论，得ED为定值，是不变的线段

如图，如果点P在线段AB上，

过点P作PF∥AC交BC于F，

由（1）证得△PFD≌△QCD，且△PBF是等边三角形

∴

∴∴ED为定值

同理，如图，若P在BA的延长线上，

作PM∥AC的延长线于M，

∴∠PMC=∠ACB，又∵AB=AC，∴∠B=∠ACB=60°，

∴∠B=∠PMC=60°，

∴PM=PB，且PE⊥BC

∴，△PBM是等边三角形∴PM=PB=CQ

∵PM∥AC

∴∠PMB=∠QCM，∠MPD=∠CQD且PM=CQ

∴△PMD≌△QCD（ASA），

∴，

∴

4、如图，AD是ABC中BC边上的中线，若AB＝5，AC＝8，则AD的取值范围是_____．

【答案】1.5<AD<6.5．

【解析】解：如图，延长AD到E，使DE=AD，
∵AD是BC边上的中线，∴BD=CD，
在△ABD和△ECD中,
∵ ，∴△ABD≌△ECD(SAS),CE=AB，
∵AB=5，AC=8，∴8-5<AE<8+5，即3<2AD<13，∴1.5<AD<6.5，

故答案为：1.5<AD<6.5．

5、某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．

（探究与发现）

（1）如图1，AD是的中线，延长AD至点E，使，连接BE，证明：．

（理解与应用）

（2）如图2，EP是的中线，若，，设，则x的取值范围是________．

（3）如图3，AD是的中线，E、F分别在AB、AC上，且，求证：．

【答案】（1）见解析；（2）；（3）见解析

【解析】（1）证明：，，，，

（2）；

如图，延长至点，使，连接，

在与中，，，，

在中，，

即，的取值范围是；故答案为：；

（3）延长FD至G，使得，连接BG，EG，

在和中，，，，

，，

在和中，

，，，

，，

在中，两边之和大于第三边

，，

又，，

6、如图，已知和中，，，，，，线段分别交，于点，．

（1）请说明的理由；

（2）可以经过图形的变换得到，请你描述这个变换；

（3）求的度数．

【答案】（1）见解析；（2）通过观察可知绕点顺时针旋转，可以得到；（3）

【解析】解：（1）∵，，，

∴，∴，，

∴，

∴；

（2）通过观察可知绕点顺时针旋转，可以得到；

（3）由（1）知，，

∴．

7、如图，，，三点在一条直线上，和均为等边三角形，与交于点，与交于点．

（1）求证：；

（2）若把绕点任意旋转一个角度，（1）中的结论还成立吗？请说明理由．

【答案】（1）见解析（2）成立，理由见解析．

【解析】解：（1）证明：如图1中，与都是等边三角形，

，，，

，

，，

即．

在和中，，(SAS)．

．即AE=BD，

（2）成立；理由如下：

如图2中，、均为等边三角形，

，，，

，

即，

在和中，，，

．

8、（1）如图，在四边形中，，，、分别是边、上的点，且．求证：；

（2）如图，在四边形中，，，、分别是边、延长线上的点，且．（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．

【答案】（1）见证明；（2）结论EF＝BE+FD不成立，应当是EF＝BE﹣FD，证明见详解．

【解析】解：（1）证明：如图，延长CB至M，使BM＝DF，连接AM．

∵∠ABC+∠D＝180°，∠1+∠ABC＝180°，∴∠1＝∠D，

在△ABM与△ADF中，

，∴△ABM≌△ADF（SAS）．∴AF＝AM，∠2＝∠3．

∵∠EAF∠BAD，∴∠2+∠4∠BAD＝∠EAF．

∴∠3+∠4＝∠EAF，即∠MAE＝∠EAF．

在△AME与△AFE中，，∴△AME≌△AFE（SAS）．

∴EF＝ME，即EF＝BE+BM，∴EF＝BE+DF；

（2）结论EF＝BE+FD不成立，应当是EF＝BE﹣FD．

证明：如图，在BE上截取BG，使BG＝DF，连接AG．

∵∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，

∴∠B＝∠ADF．

∵在△ABG与△ADF中，

，∴△ABG≌△ADF（SAS），

∴∠BAG＝∠DAF，AG＝AF，

∴∠BAG+∠EAD＝∠DAF+∠EAD＝∠EAF∠BAD，

∴∠GAE＝∠EAF．

在△AGE与△AFE中，

，∴△AEG≌△AEF，∴EG＝EF，

∵EG＝BE﹣BG，∴EF＝BE﹣FD．

9、如图1，图2，图3，在中，分别以为边，向外作正三角形，正四边形，正五边形，相交于点．（正多边形的各边相等，各个内角也相等）

①如图1，求证：△ABE≌△ADC；

②探究：如图1，∠BOD=                ；

③如图2，∠BOD=                ；

④如图3，∠BOD=                ．

【答案】①见解析；②60°；③90°；④108°

【解析】解：①证明：如图，

∵△ABD和△AEC是等边三角，
∴AD=AB，AE=AC，∠DAB=∠EAC=∠ABD=∠ADB=60°，
∴∠DAB+∠BAC=∠EAC+∠BAC，
即∠DAC=∠BAE．
在△ABE和△ADC中，

，∴△ABE≌△ADC（SAS）；

②，，

∵∠AFD=∠OFB，∴∠BOD=∠BAD=60°；

③如图， 四边形和四边形是正方形，

，，，，

，

即，

在和中，

，，，

∵∠AHB=∠OHD，∴∠BOD=∠BAD=90°；

④如图，五边形和五边形是正五边形，

，，，

，，

，

在和中，

，，，

∵∠AMB=∠OMD，∴∠BOD=∠BAD=（5-2）×180°÷5=108°．