高中人教B版 (2019)第一章　空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.4 二面角导学案及答案

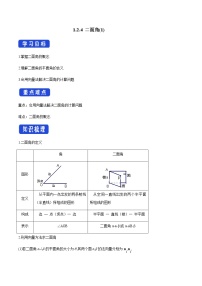
二面角

【学习目标】

1．通过学习二面角的概念及二面角的平面角，培养数学抽象素养．

2．借助求二面角的方法和步骤的学习，提升逻辑推理、数学运算素养．

【学习重难点】

1．掌握二面角的概念，二面角的平面角的定义，会找一些简单图形中的二面角的平面角．（重点）

2．掌握求二面角的方法、步骤．（重点、难点）

【学习过程】

一、新知初探

1．二面角的概念

（1）半平面：平面内的一条直线把平面分为两部分，其中的每一部分都叫做半平面．

（2）二面角：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面．棱为l，两个面分别为α，β的二面角的面，记作α­l­β，若A∈α，B∈β，则二面角也可以记作A­l­B，二面角的范围为[0，π]．

（3）二面角的平面角：在二面角α­l­β的棱上任取一点O，以O为垂足，分别在两半平面内分别作射线OA⊥l，OB⊥l，则∠AOB叫做二面角α­l­β的平面角．

2．用空间向量求二面角的大小

如果n1，n2分别是平面α1，α2的一个法向量，设α1与α2所成角的大小为θ．则θ＝〈n1，n2〉或θ＝π－〈n1，n2〉，sinθ＝sin〈n1，n2〉．

二、初试身手

1．思考辨析（正确的打“√”，错误的打“×”）

（1）二面角的范围是．（    ）

（2）若二面角α­l­β的两个半平面的法向量分别为n1，n2，则二面角的平面角与两法向量夹角〈n1，n2〉一定相等．（    ）

（3）二面角的大小通过平面角的大小来度量．（    ）

2．（教材P52练习B②改编）在正方体ABCD­A1B1C1D1中，二面角A1­BC­A的余弦值为（    ）

A．

B．

C．

D．

3．已知二面角α­l­β，其中平面α的一个法向量m＝（1,0，－1），平面β的一个法向量n＝（0，－1,1），则二面角α­l­β的大小可能为________．

4．在正方体ABCD­A1B1C1D1中，二面角A1­BD­C1的余弦值是________．

三、合作探究

类型1：用定义法求二面角

【例1】如图，设AB为圆锥PO的底面直径，PA为母线，点C在底面圆周上，若△PAB是边长为2的正三角形，且CO⊥AB，求二面角P­AC­B的正弦值．

类型2：用向量法求二面角

【例2】如图所示，四棱柱ABCD­A1B1C1D1的所有棱长都相等，AC∩BD＝O，A1C1∩B1D1＝O1，四边形ACC1A1和四边形BDD1B1均为矩形．

（1）证明：O1O⊥底面ABCD；

（2）若∠CBA＝60°，求二面角C1­OB1­D的余弦值．

类型3：空间中的翻折与探索性问题

【例3】如图甲，在直角梯形ABCD中，AB∥CD，AB⊥BC，CD＝2AB＝2BC＝4，过A点作AE⊥CD，垂足为E，现将△ADE沿AE折叠，使得DE⊥EC．取AD的中点F，连接BF，CF，EF，如图乙．

（1）求证：BC⊥平面DEC；

（2）求二面角C­BF­E的余弦值．

【学习小结】

1．学会利用空间向量求二面角与定义法求二面角的方法．

2．利用向量法求二面角的基本思想是把空间角转化为求两个向量之间的关系．首先要找出并利用空间直角坐标系或基向量（有明显的线面垂直关系时尽量建系）表示出向量，然后运用向量的运算即可，其次要理清要求角与两个向量夹角之间的关系．

【精炼反馈】

1．三棱锥A­BCD中，平面ABD与平面BCD的法向量分别为n1·n2，若〈n1，n2〉＝，则二面角A­BD­C的大小为（    ）

A．

B．

C．或

D．或

2．已知△ABC和△BCD均为边长为a的等边三角形，且AD＝a，则二面角A­BC­D的大小为（    ）

A．30°

B．45°

C．60°

D．90°

3．如图所示，在正四棱锥P­ABCD中，若△PAC的面积与正四棱锥的侧面面积之和的比为∶8，则侧面与底面所成的二面角为（    ）

A． B．

C． D．

4．在正方体ABCD­A1B1C1D1中，E为BB1的中点，则平面A1ED与平面ABCD所成的锐二面角的余弦值为________．

5．三棱锥P­ABC，PA＝PB＝PC＝，AB＝10，BC＝8，CA＝6，求二面角P­AC­B的大小．